
Nghiên cứu mới nhất của Paradigm: pm-AMM - nhà tạo lập thị trường tự động thống nhất chuyên dụng cho thị trường dự đoán
Tuyển chọn TechFlowTuyển chọn TechFlow

Nghiên cứu mới nhất của Paradigm: pm-AMM - nhà tạo lập thị trường tự động thống nhất chuyên dụng cho thị trường dự đoán
AMM và tiền thân của nó (như các quy tắc định giá thị trường) ban đầu được phát minh như một cách để cung cấp thanh khoản cho thị trường dự đoán.
Tác giả: Ciamac Moallemi, Dan Robinson, Paradigm
Biên dịch: Yangz, Techub News
Giới thiệu
Trong bài viết này, chúng tôi giới thiệu một loại thị trường tạo lập tự động (AMM) mới được thiết kế riêng cho thị trường dự đoán: pm-AMM.
Các AMM và tiền thân của chúng (ví dụ như quy tắc điểm thị trường) ban đầu được phát minh nhằm cung cấp thanh khoản cho các thị trường dự đoán. Hiện nay, chúng chiếm đa số khối lượng giao dịch trên hầu hết các DEX. Tuy nhiên, điều trớ trêu là mặc dù khối lượng giao dịch trên thị trường dự đoán đang tăng mạnh, phần lớn trong số đó lại sử dụng sổ lệnh thay vì AMM.
Một trong những lý do có thể là các AMM hiện tại không phù hợp với các token kết quả (tức là token có giá 1 đô la nếu sự kiện xảy ra và 0 đô la nếu không). Biến động giá của token kết quả phụ thuộc vào xác suất hiện tại của sự kiện và thời gian đến hạn của thị trường dự đoán, dẫn đến tính thanh khoản mà nhóm thanh khoản cung cấp là không ổn định. Khi thị trường dự đoán đáo hạn, nhà cung cấp thanh khoản (LP) về cơ bản sẽ mất toàn bộ giá trị.
Vì vậy, chúng tôi đề xuất một loại AMM mới được tối ưu hóa xung quanh những yếu tố này, nhằm giải quyết một vấn đề lâu dài trong nghiên cứu AMM: Tối ưu hóa AMM cho một loại tài sản cụ thể có nghĩa là gì? Nói cách khác, khi đã có mô hình cho một loại tài sản nhất định (như quyền chọn, trái phiếu, stablecoin hay token kết quả), điều đó ảnh hưởng thế nào đến việc lựa chọn AMM? Chúng tôi đưa ra câu trả lời khả thi dựa trên khái niệm "lỗ so với tái cân bằng" (LVR).
Kết quả nghiên cứu
Chúng tôi xây dựng một mô hình cho biến động giá của một số token kết quả, gọi là động thái điểm Gauss (Gaussian score dynamics). Mô hình này có thể áp dụng cho thị trường dự đoán, dùng để dự đoán liệu một quá trình ngẫu nhiên cơ bản (như khoảng cách điểm số trong trận bóng rổ, chênh lệch phiếu bầu trong bầu cử, hoặc giá một tài sản nào đó) tại thời điểm đáo hạn có vượt qua một ngưỡng nhất định hay không.
Dựa trên mô hình này, chúng tôi suy ra một dạng AMM bất biến mới dành cho các token này — gọi là bất biến pm-AMM tĩnh:
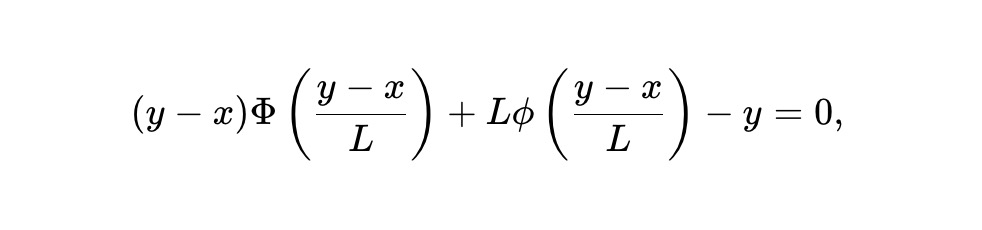
Trong đó, x là dự trữ token kết quả trong AMM, y là dự trữ token kết quả bổ sung đối ứng, L là tổng thanh khoản hoặc hệ số tỷ lệ, ϕ và Φ lần lượt là hàm mật độ xác suất và hàm phân phối tích lũy của phân phối chuẩn.
Bất biến trên dựa trên một khái niệm mạnh mẽ: "lỗ so với tái cân bằng" (Loss vs Rebalancing - LVR), có thể hiểu là tỷ lệ thua lỗ của AMM do bị arbitrage. LVR phụ thuộc vào hình dạng của AMM và sự biến động giá của tài sản được giao dịch trên AMM.
Chúng tôi định nghĩa một AMM đồng nhất (uniform AMM) là loại AMM có LVR kỳ vọng luôn tỉ lệ thuận với giá trị danh mục đầu tư tại mọi mức giá hiện tại. Như Milionis và cộng sự chỉ ra, đối với tài sản có giá tuân theo chuyển động Brown hình học (GBM — mô hình phổ biến cho cổ phiếu và tài sản mã hóa), các nhà tạo lập thị trường trung bình hình học hằng định (như Uniswap và Balancer) là duy nhất là AMM đồng nhất; còn static pm-AMM là AMM đồng nhất cho các tài sản tuân theo mô hình động điểm Gauss mà chúng tôi đề xuất.
Mặc dù static pm-AMM có LVR đồng nhất tại mọi mức giá, LVR vẫn tăng lên khi ngày đáo hạn đến gần, vì thị trường dự đoán trở nên rất biến động khi gần tới thời điểm kết thúc. Để điều chỉnh pm-AMM giảm thanh khoản theo thời gian sao cho LVR kỳ vọng giữ nguyên trong suốt thời gian còn lại trước khi đáo hạn, chúng tôi suy ra bất biến dynamic pm-AMM, phụ thuộc vào thời gian còn lại T-t:
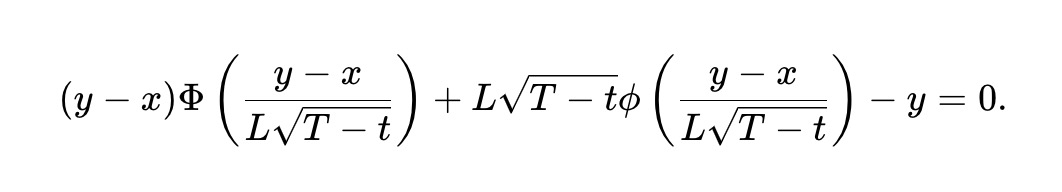
Cơ chế dynamic pm-AMM ngăn chặn việc LVR tăng lên khi gần đáo hạn bằng cách cung cấp thanh khoản ngày càng giảm. Trong các nhóm thực tế, điều này có thể không mong muốn, đặc biệt khi hoạt động giao dịch phi arbitrage (và do đó là phí giao dịch) có thể gia tăng theo thời gian. Tuy nhiên, pm-AMM cung cấp một khuôn khổ giúp nhà cung cấp thanh khoản điều chỉnh thanh khoản dựa trên phí kỳ vọng và cách họ muốn phân bổ rủi ro arbitrage.
Các AMM này có thể hỗ trợ dẫn dắt thanh khoản thụ động trên các thị trường dự đoán chuỗi khối. Khái niệm AMM đồng nhất và phương pháp liên quan cũng có thể mở rộng cho các nhà thiết kế DEX, giúp họ tùy chỉnh AMM cho các loại tài sản khác có hành vi giá không tuân theo GBM, ví dụ như stablecoin, trái phiếu, quyền chọn hay các công cụ phái sinh khác.
Hình 1 thể hiện đường cong bất biến của static và dynamic pm-AMM, so sánh với hai dạng bất biến nổi tiếng khác: nhà tạo lập thị trường tích hằng định (CPMM) và quy tắc điểm thị trường logarit (LMSR). Lưu ý rằng dynamic pm-AMM cung cấp ít thanh khoản hơn theo thời gian.
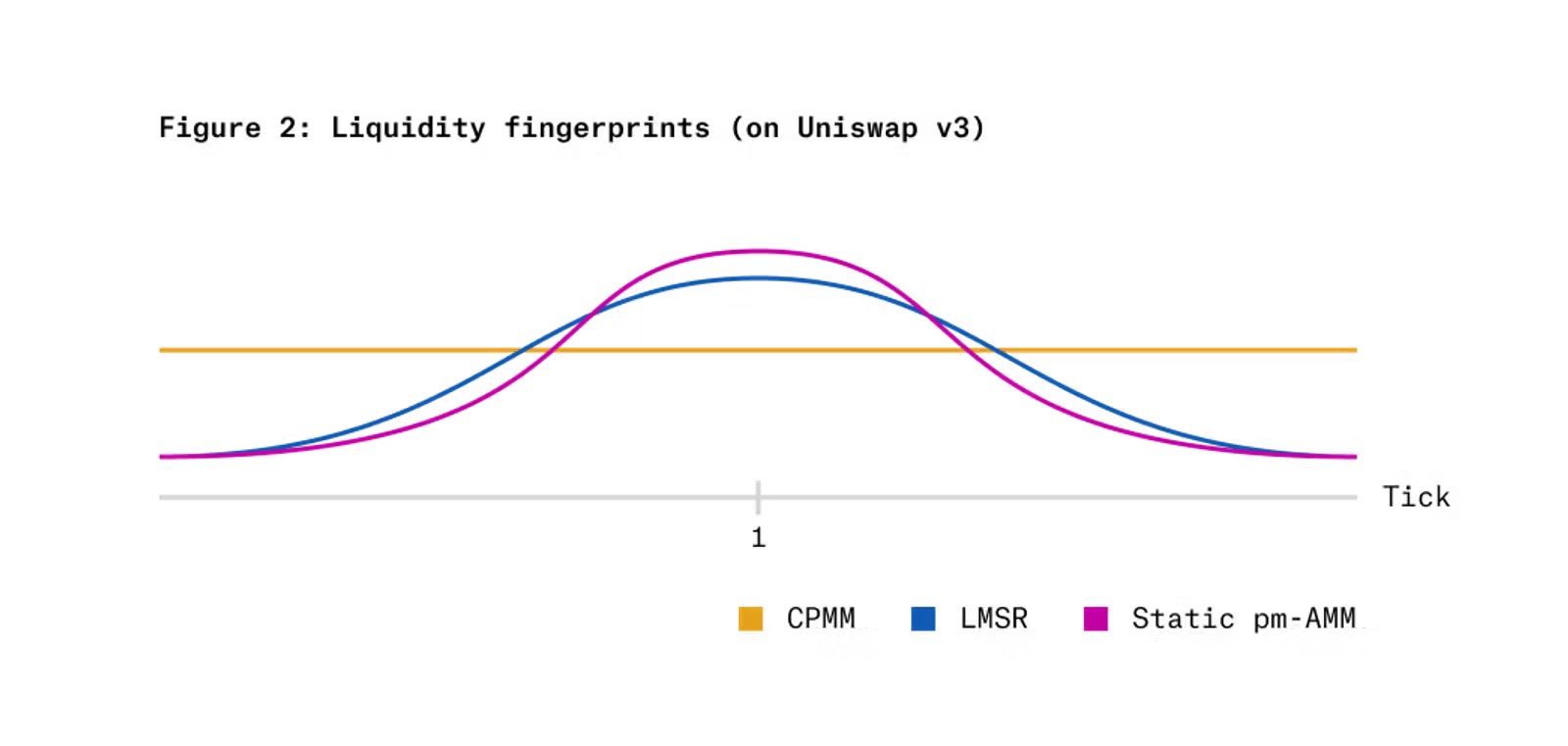
Hình 2 thể hiện "dấu vân tay thanh khoản" (liquidity fingerprint) khi áp dụng bất biến static pm-AMM trên AMM tập trung thanh khoản Uniswap v3, so với CPMM và LMSR. Trục hoành biểu diễn thang log của giá tương đối (giá token x chia cho giá token y), trục tung biểu diễn thanh khoản của từng AMM tại mức giá đó. Có thể thấy, so với hai phương án thay thế, pm-AMM tập trung nhiều thanh khoản hơn ở mức giá tương đối bằng 1 (xác suất 50%, tức giá token là 0.50), nhưng cung cấp ít thanh khoản hơn ở các mức giá cực đoan (rất thấp hoặc rất cao).
Ngữ cảnh nghiên cứu
Thị trường dự đoán
Thị trường dự đoán ngày càng trở nên phổ biến trong lĩnh vực tiền mã hóa. Riêng tháng 10 năm 2024, khối lượng giao dịch trên Polymarket đã vượt quá 2 tỷ đô la Mỹ. Tuy nhiên, phần lớn thanh khoản trên các thị trường dự đoán mã hóa được cung cấp thông qua sổ lệnh chứ không phải AMM, dù AMM đang thống trị khối lượng giao dịch trên hầu hết DEX.
Một lý do có thể là hành vi giá của token kết quả khác biệt so với tài sản thông thường, khiến AMM được thiết kế cho chúng hoạt động không ổn định. Ví dụ, hãy tưởng tượng một thị trường dự đoán về trò chơi tung đồng xu, trong đó ai đó tung đồng xu 1001 lần, mỗi mặt (ngửa/sấp) tương ứng với token x và y. Cuối cùng, nếu mặt ngửa nhiều hơn thì token x trị giá 1 đô la, ngược lại là 0 đô la; token y thì ngược lại.
Độ biến động của các token kết quả này phụ thuộc lớn vào số lần tung còn lại và tình trạng hiện tại. Tình huống càng sát sao và số lần tung còn lại càng ít, các token này càng biến động mạnh. Điều này có nghĩa là tổn thất từ nhà tạo lập thị trường tích hằng định (được mô tả bên dưới, phụ thuộc vào độ biến động) thay đổi rất lớn theo thời gian.
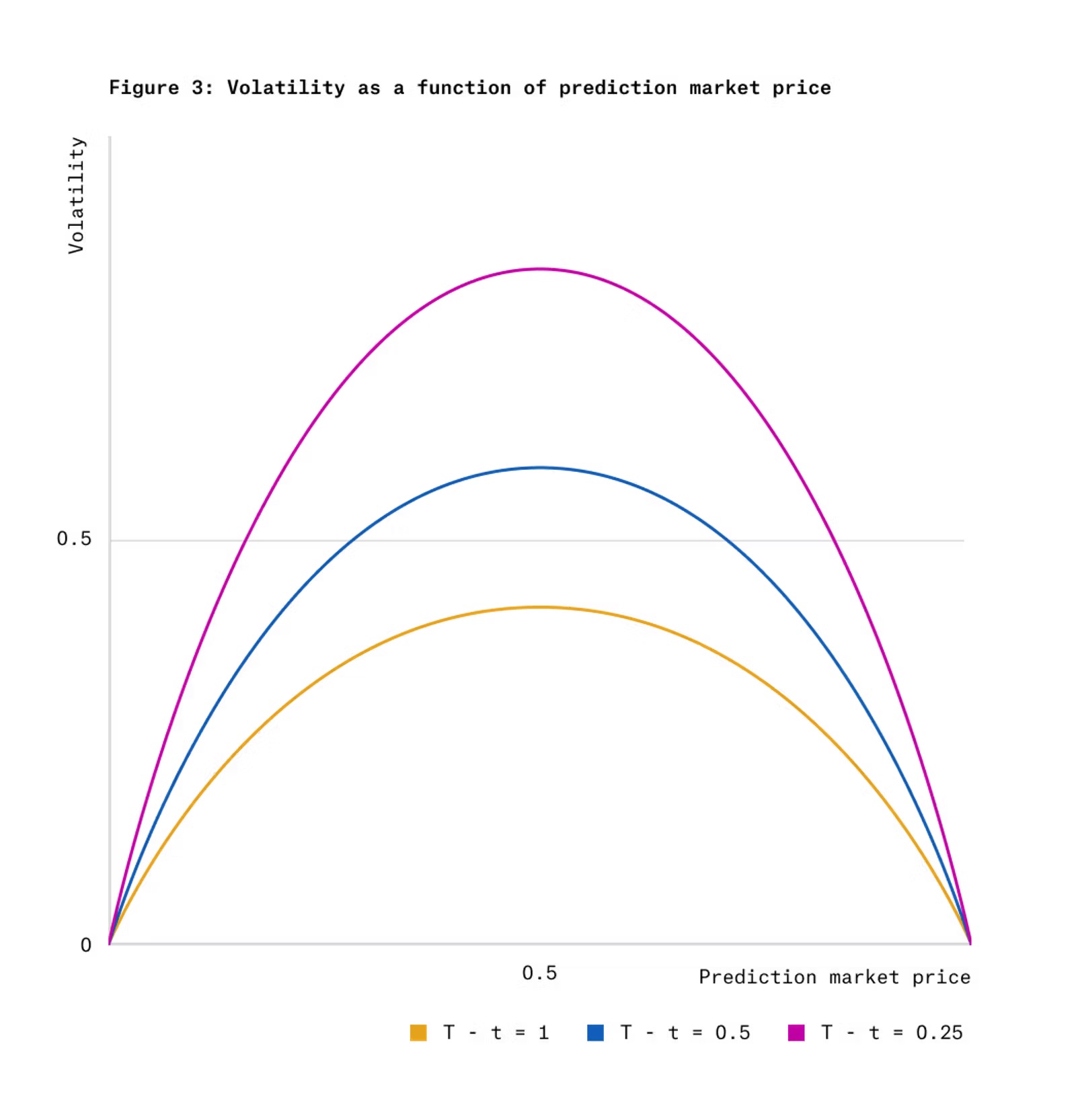
Hình 3 thể hiện độ biến động giá của token kết quả theo mô hình động điểm Gauss, phụ thuộc vào giá token và thời gian còn lại.
Nhiều thị trường dự đoán phổ biến tương tự ví dụ tung đồng xu này — đặt cược vào việc một quá trình ngẫu nhiên cơ bản tại thời điểm đáo hạn có vượt 0 hay không. Ví dụ:
-
Thị trường dự đoán kết quả trận bóng rổ sẽ đáo hạn khi thời gian trận đấu kết thúc. Quá trình ngẫu nhiên là chênh lệch điểm số giữa hai đội.
-
Thị trường dự đoán kết quả bầu cử tổng thống sẽ đáo hạn vào ngày bầu cử. Quá trình ngẫu nhiên là chênh lệch số cử tri bỏ phiếu cho các ứng viên.
-
Thị trường dự đoán giá tài sản như Bitcoin tại một thời điểm trong tương lai có cao hơn một mức giá thực thi hay không, trong đó quá trình ngẫu nhiên có thể là logarit của giá Bitcoin hiện tại trừ đi mức giá thực thi.
Mô hình biến động giá của token kết quả mà chúng tôi định nghĩa trong bài viết này — động điểm Gauss — lấy cảm hứng từ các ví dụ như vậy. Mô hình giả định rằng giá thị trường dự đoán khớp với xác suất quá trình Brown tiềm ẩn kết thúc trên 0. Mô hình này tương tự mô hình Black-Scholes cho quyền chọn nhị phân (một công cụ chi trả cố định nếu giá tài sản vượt mức thực thi, và 0 nếu không). Tuy nhiên, trong mô hình của chúng tôi, quá trình tiềm ẩn không cần tương ứng với giá tài sản có thể giao dịch.
Chúng tôi đưa ra một giả định đơn giản hóa rằng giá token kết quả bằng đúng xác suất nó sẽ trả 1 đô la. Giả định này bỏ qua các đặc điểm quan trọng của thị trường như rủi ro và sở thích theo thời gian, do đó việc nghiên cứu tác động của các yếu tố này sẽ là chủ đề cho các nghiên cứu trong tương lai.
Hơn nữa, không phải tất cả thị trường dự đoán đều phù hợp với mô hình động điểm Gauss, vì mô hình này giả định tốc độ xuất hiện thông tin mới là có thể dự đoán được. Ví dụ, bóng rổ có thể phù hợp hơn bóng đá vì tần suất ghi điểm cao hơn, khiến chênh lệch điểm số tiến triển ổn định hơn theo thời gian. Ngoài ra, một số loại thị trường dự đoán hoàn toàn khác với mô hình này, ví dụ như dự đoán liệu một sự kiện đơn lẻ (như động đất) có xảy ra trước một ngày nhất định hay không. Tuy nhiên, mô hình này có thể là điểm khởi đầu hữu ích để suy luận các mô hình động lực học khác, đồng thời minh họa phương pháp suy ra AMM đồng nhất cho bất kỳ mô hình nào.
Lỗ so với tái cân bằng và tính đồng nhất
Sau khi làm rõ mô hình, chúng tôi suy ra một cơ chế có thể phù hợp hơn với các token này so với các AMM hiện tại (như CPMM hay LMSR). Chỉ số hướng dẫn chúng tôi là tỷ lệ tổn thất kỳ vọng của nhà cung cấp thanh khoản, được gọi là "lỗ so với tái cân bằng" (LVR).
LVR phản ánh chi phí nghịch chiều chính của AMM: khi không có giao dịch, giá AMM là tĩnh, nhưng khi thông tin mới xuất hiện, giá trở nên lỗi thời. LVR thể hiện chi phí mà nhà cung cấp thanh khoản phải chịu khi các trader am hiểu thông tin hơn tận dụng các mức giá lỗi thời này để thực hiện giao dịch arbitrage bất lợi cho AMM. Vì vậy, LVR có thể coi là khoản phí mà AMM trả cho các nhà arbitrage để điều chỉnh lại giá.
Hơn nữa, trong trường hợp không có phí giao dịch, LVR cũng chính là tổn thất mà nhà LP gặp phải khi phòng ngừa rủi ro Delta bằng cách nắm giữ vị thế bán khống đúng bằng số lượng token trong nhóm thanh khoản. Do đó, LVR dựa trên nhận định chính của mô hình định giá quyền chọn Black-Scholes. Cũng như việc phòng ngừa rủi ro Delta loại bỏ rủi ro thị trường đối với quyền chọn, LVR định giá vị thế LP trong AMM sau khi loại bỏ rủi ro thị trường. Nghĩa là, LVR cô lập rủi ro đặc thù khi làm nhà cung cấp thanh khoản trong AMM, chứ không đơn thuần là rủi ro nắm giữ danh mục giống như AMM.
Chúng tôi xét các AMM bất biến đơn giản, không có phí hay cơ chế thu hồi MEV. Trong trường hợp này, AMM chắc chắn sẽ thua lỗ do arbitrage, và không tồn tại bất kỳ bất biến AMM nào có thể loại bỏ LVR (trừ phi dẫn đến không có giao dịch nào xảy ra). Hơn nữa, kể cả "tối thiểu hóa" LVR cũng không thực tiễn, vì giảm LVR đồng nghĩa với giảm thanh khoản cung cấp.
Tuy nhiên, dù không thể loại bỏ LVR, chúng ta có thể làm cho LVR mang tính đồng nhất hơn, nghĩa là tỷ lệ phần trăm giá trị nhóm bị mất đi sẽ không phụ thuộc vào giá hiện tại của tài sản. Chúng tôi gọi đặc tính này là tính đồng nhất (uniformity).
Hãy tưởng tượng một nhà tài trợ sẵn sàng cung cấp thanh khoản miễn phí trên một thị trường dự đoán để hiểu dự báo của thị trường về kết quả. Nhà tài trợ này sẽ thua tiền, nhưng họ muốn phân bổ tổn thất một cách đồng đều thay vì tập trung vào một thời điểm hay mức giá cụ thể. Trong trường hợp này, giá trị hiện tại của nhóm thanh khoản có thể được xem là "ngân sách" của nhà tài trợ. Trên một AMM đồng nhất, nếu nhà tài trợ đóng góp 1 đô la thanh khoản tại một thời điểm, tổn thất kỳ vọng tại thời điểm tiếp theo sẽ không phụ thuộc vào trạng thái hiện tại của nhóm.
Hơn nữa, tính đồng nhất cũng có ý nghĩa tiềm tàng đối với các nhà cung cấp thanh khoản theo đuổi lợi nhuận. Ngay cả khi AMM có thể thu hồi một phần lợi nhuận từ LVR, thậm chí hòa vốn hay có lãi (qua phí hoán đổi dương hoặc cơ chế đấu giá như thuế MEV), họ vẫn cần chiến lược để phân bổ thanh khoản tại các mức giá và thời điểm khác nhau. Ta có thể xem tổn thất kỳ vọng của nhóm không phí như một thước đo để quyết định phân bổ bao nhiêu thanh khoản tại một thời điểm, với sự cân nhắc đến quá trình giá của tài sản.
Chúng tôi định nghĩa AMM đồng nhất cho một tài sản cụ thể là AMM có LVR kỳ vọng luôn là một tỷ lệ cố định so với giá trị hiện tại của nhóm thanh khoản, bất kể giá hiện tại của tài sản là bao nhiêu. Lưu ý rằng việc AMM có LVR đồng nhất hay không phụ thuộc vào chính quá trình giá của tài sản đó. Như Milionis và cộng sự chỉ ra trong Phụ lục B.2, nếu giá tài sản tuân theo chuyển động Brown hình học, thì AMM đồng nhất cơ bản duy nhất là nhà tạo lập thị trường trung bình hình học có trọng số, với bất biến:
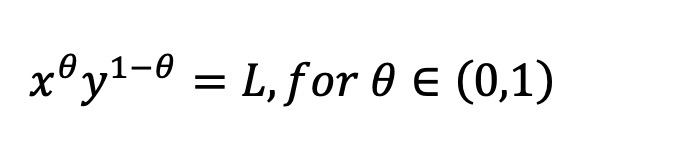
Đây là công thức được Balancer sử dụng, còn nhà tạo lập thị trường tích hằng định trong Uniswap v2 là một trường hợp đặc biệt. Tuy nhiên, đối với các token tuân theo động điểm Gauss, nhà tạo lập trung bình hình học hằng định không có LVR đồng nhất. Quy tắc điểm thị trường logarit (LMSR) cũng vậy.
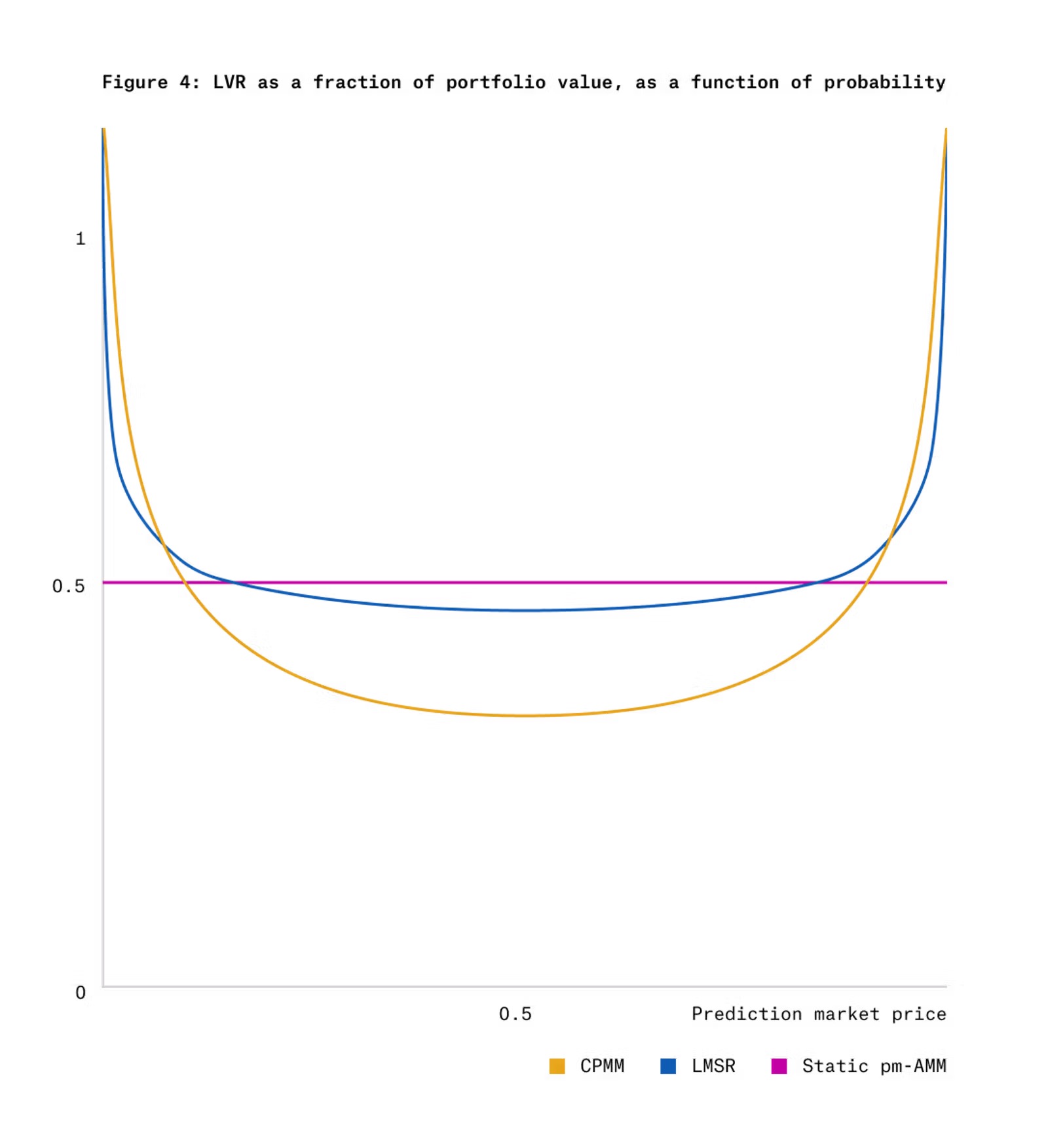
Hình 4 thể hiện LVR của CPMM và LMSR so với LVR đồng nhất của static pm-AMM, khi dùng cho token kết quả theo động điểm Gauss tại thời điểm T-t=1.
Vì những lý do trên, chúng tôi phát triển hai loại AMM dành cho thị trường dự đoán theo động điểm Gauss: một loại có LVR đồng nhất tại mọi thời điểm nhưng LVR tăng dần khi gần đáo hạn; loại kia có LVR đồng nhất và LVR kỳ vọng không đổi trong suốt thời gian còn lại.
Từ Hình 4, có thể thấy CPMM và LMSR có LVR lớn khi giá token kết quả ở mức cực đoan (gần 0 hoặc 1). Điều này xảy ra vì dù biến động giá gần các điểm này thấp (xem Hình 3), tốc độ suy giảm giá trị nhóm lại nhanh hơn ở mức giá cực đoan. Do đó, một AMM đồng nhất nên cung cấp ít thanh khoản hơn ở mức giá cực đoan — đúng như thiết kế của pm-AMM (xem Hình 2).
Nghiên cứu trước đó
AMM bắt nguồn từ thị trường dự đoán và các quy tắc điểm thị trường (như LMSR). Những quy tắc này dẫn đến sự ra đời của các nhà tạo lập thị trường hàm hằng (CFMM), như Uniswap v2, nổi bật bởi mối quan hệ bất biến giữa các dự trữ tài sản trong AMM. Các AMM dựa trên thiết kế này đã trở thành cơ chế thị trường chủ đạo trên DEX trong những năm gần đây.
Gần đây, góc nhìn kinh tế tài chính được áp dụng để hiểu chi phí của AMM, dưới dạng LVR, chủ yếu tập trung vào chuyển động Brown hình học. Mặt khác, động lực học giá trên thị trường dự đoán rất khác biệt do lợi nhuận giới hạn và thời hạn cố định. Taleb đề xuất động lực học dựa trên quá trình biểu quyết quan sát được, còn chúng tôi phát triển một dạng khác dựa trên quá trình điểm Gauss quan sát được.
Trước đây đã có một số nghiên cứu ứng dụng về thiết kế AMM cho tài sản không theo GBM. Một ví dụ là StableSwap — AMM dành cho cặp stablecoin, được xây dựng trên tiền đề trực quan rằng AMM giữa các tài sản liên quan và tài sản hồi quy trung bình nên tập trung thanh khoản chặt chẽ quanh một mức giá, nhưng suy luận của nó không liên quan đến mô hình hóa quá trình giá tài sản. Một ví dụ khác là YieldSpace — AMM dành riêng cho trái phiếu không coupon. Mặc dù YieldSpace có suy luận dựa trên mô hình định giá trái phiếu đơn giản, nhưng nó không bao gồm mô hình đầy đủ về quá trình giá (không mô hình hóa sự thay đổi lãi suất).
Hơn nữa, trong giới học thuật cũng có các nghiên cứu thiết kế mô hình thị trường theo niềm tin về hành vi giá tài sản. Một ví dụ là khung của Goyal và cộng sự. Khung của họ được thiết kế nhằm tối đa hóa thanh khoản hoạt động kỳ vọng, chứ không nhằm làm cho tổn thất kỳ vọng đồng nhất, do đó đôi khi đưa ra kết luận ngược lại với chúng tôi. Ví dụ, họ cho rằng nếu nhà cung cấp thanh khoản kỳ vọng giá tương đối của tài sản sẽ dao động quanh 1, thì LMSR (so với CPMM, tập trung thanh khoản quanh giá 1) là phù hợp; trong khi khung của chúng tôi cho rằng nếu kỳ vọng giá phân hóa (như token kết quả), thì nên tập trung thanh khoản quanh 1.
Các mô hình AMM
Thị trường tạo lập tự động (AMM)
Xét một thị trường dự đoán về một sự kiện đơn lẻ và một AMM giao dịch hai tài sản đối nghịch. Tài sản rủi ro x thanh toán 1 đô la nếu sự kiện xảy ra, ngược lại là 0; tài sản y thanh toán ngược lại. AMM duy trì bất biến f(x,y)=L, trong đó f(·,·) là hàm bất biến của dự trữ (x,y), L là hằng số. Với giá P của tài sản x (theo đô la), hàm giá trị nhóm là:
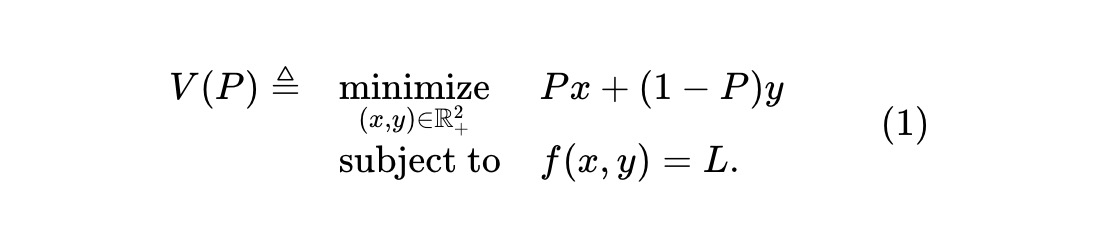
Đây là giá trị nhóm tại giá x là P. Vì nắm giữ một đơn vị x và y tương đương với nắm giữ tiền mặt, giá y phải là 1-P. Giả sử có các nhà arbitrage quan sát giá Pt của x (và 1-Pt của y) tại mỗi thời điểm t. Không có phí hay ma sát, họ liên tục giám sát AMM và tận dụng mọi định giá sai để kiếm lời. Khi tối đa hóa lợi nhuận, họ giao dịch với AMM để giảm thiểu giá trị dự trữ. Nếu ký hiệu Vt là giá trị dự trữ tại thời điểm t (khi giá là Pt), thì Vt = V(Pt).
Ví dụ 1: Với nhà tạo lập thị trường tích hằng định (CPMM), bất biến là f(x,y)≜xy, hàm giá trị nhóm là:
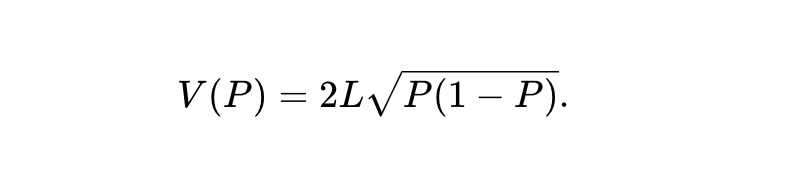
Ví dụ 2: Quy tắc điểm thị trường logarit (LMSR) do Robin Hanson tạo ra có thể được xem là AMM thỏa mãn bất biến sau:
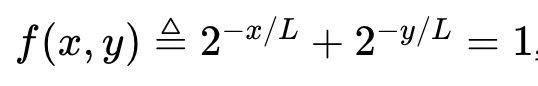
Hàm giá trị nhóm là (tỷ lệ với entropy nhị phân của sự kiện ngầm định bởi giá):
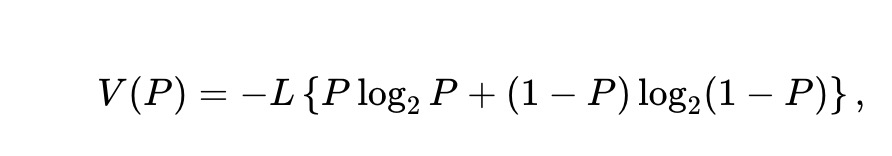
Gọi x*(P) và y*(P) là nghiệm tối ưu của bài toán (1), giả sử chúng tồn tại, duy nhất và là hàm trơn theo giá P, thì công thức sau tương tự Định lý 1 của Milionis và cộng sự, nhưng áp dụng cho môi trường hiện tại:
Định lý 1. Với mọi giá P≥0, hàm giá trị nhóm thỏa mãn:
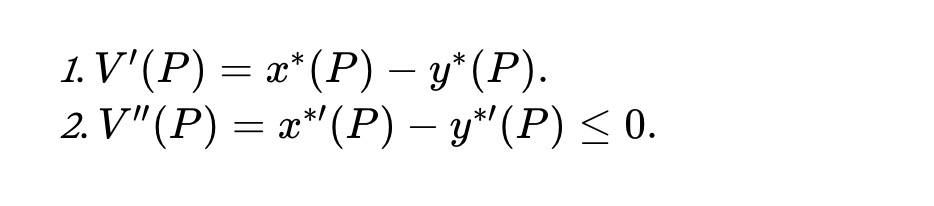
Động điểm Gauss
Giá tài sản rủi ro thay đổi thế nào theo động điểm Gauss mà chúng tôi đề cập? Cụ thể, giả sử tồn tại một quá trình ngẫu nhiên {Zt} trong khoảng thời gian t∈[0,T], sự kiện được xác định bởi dấu của Zt tại thời điểm T: nếu ZT≥0 thì x thanh toán, nếu ZT<0 thì y thanh toán. Ta có thể hiểu Zt là khoảng cách điểm số giữa hai đội trong một cuộc cạnh tranh hai bên. Vì vậy, chúng tôi gọi Zt là quá trình điểm số. Lưu ý rằng dù mô hình giả định tồn tại quá trình điểm số này, AMM không cần quan sát trực tiếp. Như mô tả bên dưới, AMM có thể suy ra giá trị hiện tại của điểm số từ giá biên (sau arbitrage) và thời gian đáo hạn.
Chúng tôi giả định Zt tuân theo biến động ngẫu nhiên. Cụ thể, giả sử Zt là chuyển động Brown với độ biến động σ>0, tức là dZt=σdBt, với Bt là chuyển động Brown tiêu chuẩn. Khi đó, dễ thấy giá Pt của tài sản x tại thời điểm t là:
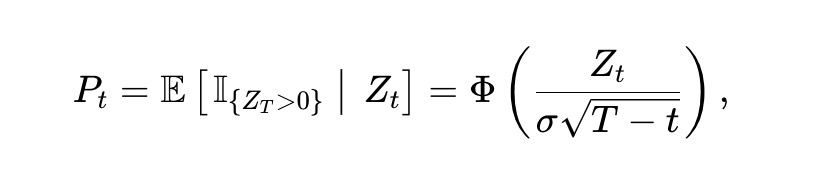
Trong đó, Φ(·) là hàm phân phối tích lũy chuẩn (CDF). Áp dụng định lý Itô, Pt phải thỏa mãn:
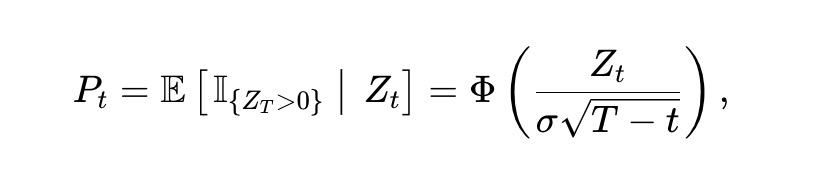
Trong đó, ϕ(·) là hàm mật độ xác suất chuẩn, Φ⁻¹(·) là hàm CDF ngược. Lưu ý rằng dù động lực học điểm số và phép chuyển đổi từ điểm sang giá (hoặc ngược lại) phụ thuộc vào σ, nhưng động lực học giá Pt độc lập với σ. Độ biến động của động lực học này theo giá và thời gian còn lại được thể hiện trong Hình 3.
AMM đồng nhất
Theo thảo luận trên, nếu ký hiệu Vt là giá trị dự trữ nhóm tại thời điểm t (khi giá là Pt), thì Vt=V(Pt). Áp dụng định lý Itô, ta có sự thay đổi giá trị nhóm như sau:
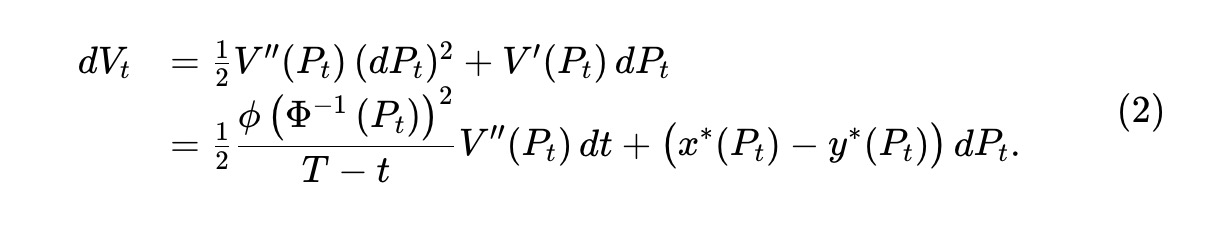
Vì giá Pt là một martingale, hạng tử thứ hai của (2) cũng là martingale, có thể tăng hoặc giảm. Tuy nhiên, theo V(·) (xem Định lý 1), hạng tử đầu tiên tương ứng với sự chuyển hóa âm, do đó là một quá trình giảm dần. Đây chính là quá trình "lỗ so với tái cân bằng" mà Milionis và cộng sự đề xuất, phản ánh giá trị bị mất do các giao dịch hedge bất lợi từ các nhà arbitrage. Chúng tôi định nghĩa tốc độ tổn thất tức thời là:
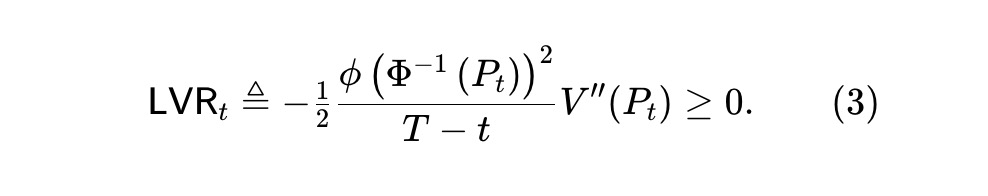
Milionis và cộng sự phát hiện rằng với tài sản tuân theo GBM, về cơ bản chỉ có nhà tạo lập trung bình hình học mới là AMM đồng nhất. Trong thị trường dự đoán theo động điểm Gauss, để kiểm tra (3), AMM đồng nhất LVR phải giải phương trình vi phân thường (ODE) sau:
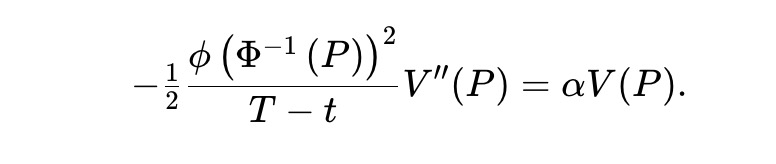
Việc này là không thể vì vế trái phụ thuộc t, còn vế phải thì không. Vấn đề cốt lõi là động lực học GBM bất biến theo thời gian, còn động điểm Gauss lại phụ thuộc mạnh vào thời gian.
Để khắc phục, chúng tôi cho phép α phụ thuộc thời gian, cụ thể đặt α=β/(T-t), với β>0, do đó xét thiết lập:
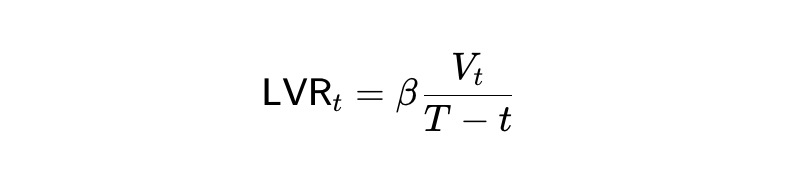
Điều này tương đương với ODE với P≥0. Ngoài ra, V(·) còn có thêm yêu cầu như V''(P)≤0 (xem Định lý 1).
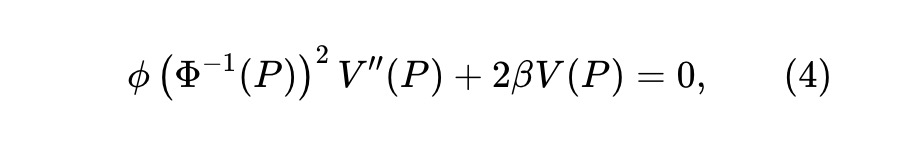
Static pm-AMM
Thay đổi biến u=Φ⁻¹(P) để đơn giản hóa ODE trên. Khi β=1/2, tồn tại nghiệm vừa thỏa mãn ODE vừa thỏa mãn điều kiện lõm bổ sung:
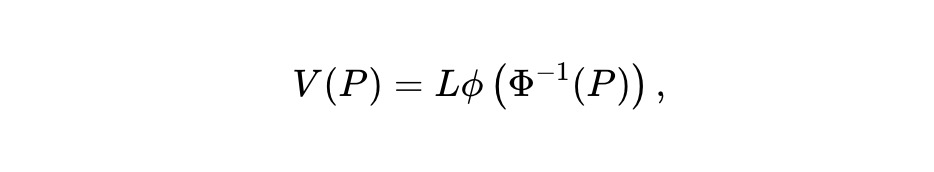
Dự trữ token x và y là:
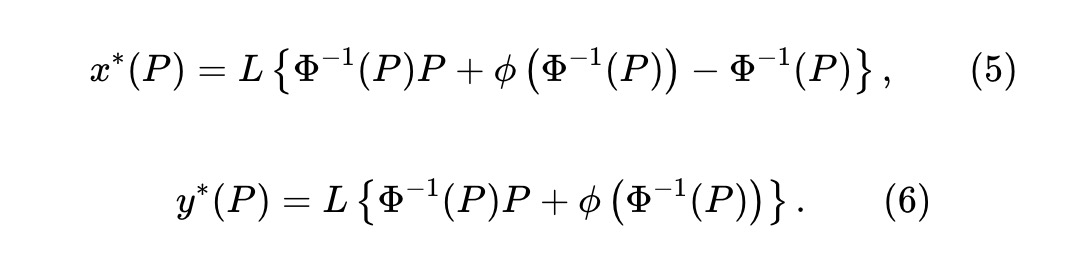
Tại đây, L≥0 là tham số thanh khoản, xác định quy mô nhóm. Quan sát y*(P)-x*(P)=LΦ⁻¹(P), thay vào (5), dự trữ (x,y) phải thỏa mãn bất biến:
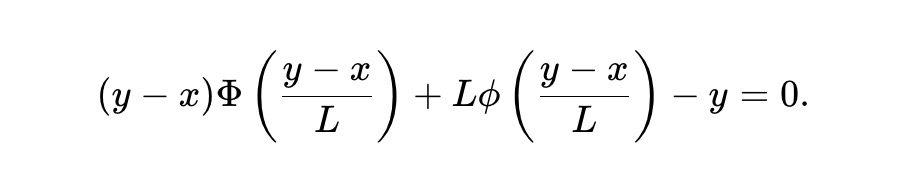
Đây chính là định nghĩa của static pm-AMM. Theo thiết kế, AMM này thỏa mãn:
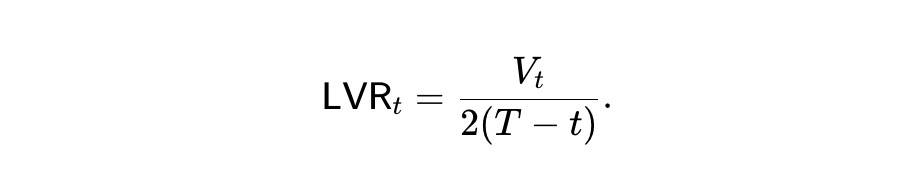
Đặt V̄t=E[Vt] là giá trị nhóm kỳ vọng, từ (2) suy ra:
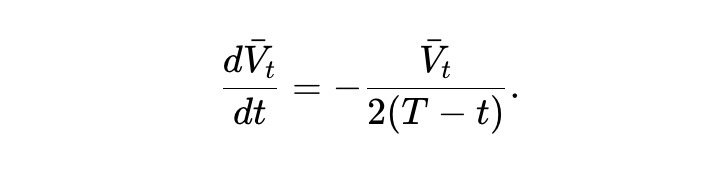
Giải ODE này, ta được kết quả sau. Nói cách khác, về kỳ vọng, giá trị nhóm của static pm-AMM suy giảm theo căn bậc hai của thời gian còn lại.
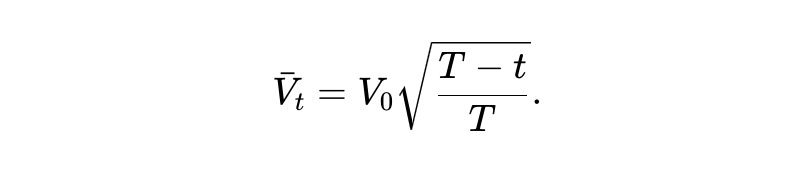
Dynamic pm-AMM
Một nhược điểm của static pm-AMM là dù LVR trên mỗi đô la giá trị là đồng nhất tại mọi giá, nó vẫn thay đổi theo thời gian. Đặc biệt, tổn thất mỗi đô la tăng nghịch với thời gian đáo hạn, do đó tăng dần theo thời gian và mất toàn bộ giá trị khi đáo hạn.
Thanh khoản động. Chúng tôi hình dung một biến thể động của thiết kế static pm-AMM, trong đó các LP rút thanh khoản theo thời gian để giảm tổn thất. Cụ thể, giả sử giá trị nhóm là:
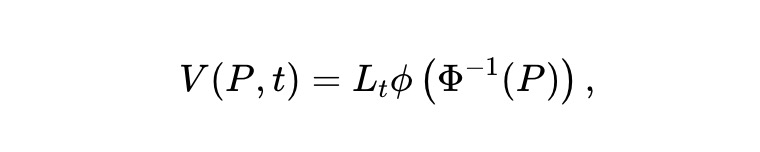
Trong đó, Lt là hàm trơn xác định, điều khiển mức độ thanh khoản bị rút (hoặc có thể tăng) theo thời gian. Áp dụng định lý Itô vào quá trình giá trị nhóm Vt≜V(Pt,t), ta có:
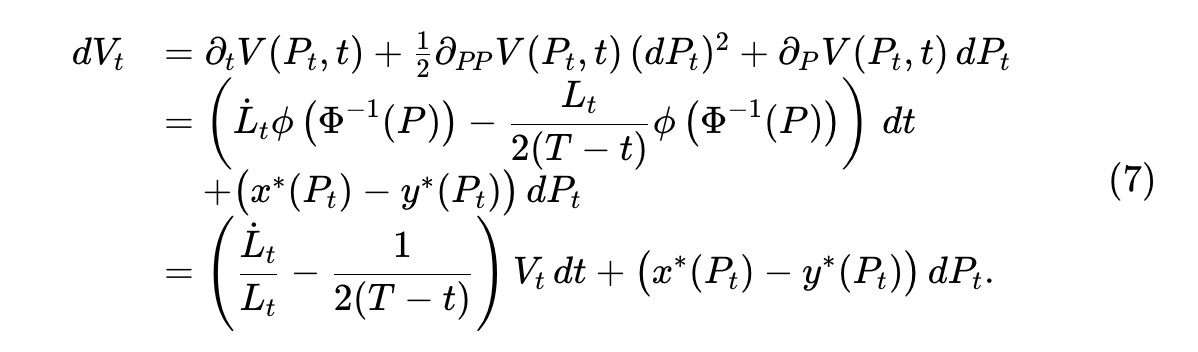
Gọi Ct là giá trị tích lũy rút ra tính theo đô la. Vì giá trị nhóm tuyến tính với thanh khoản Lt, giá trị rút ra tính bằng đô la tỷ lệ với Vt/Lt. Ta có:
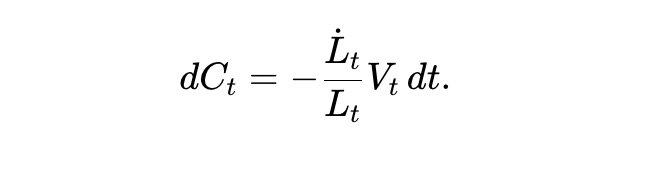
Tổng tài sản Wt của LP AMM bao gồm giá trị dự trữ và giá trị tích lũy rút ra, do đó Wt=Vt+Ct, và thỏa mãn:
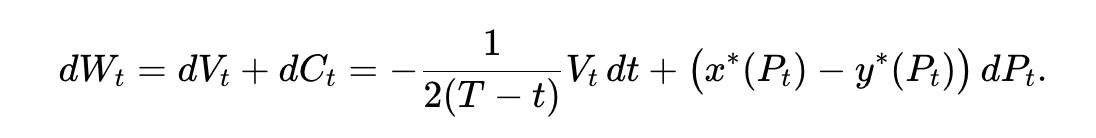
Điều này có nghĩa là tài sản kỳ vọng của LP W̄t≜E[Wt] thỏa mãn điều kiện sau, với V̄t≜E[Vt].
Chào mừng tham gia cộng đồng chính thức TechFlow
Nhóm Telegram:https://t.me/TechFlowDaily
Tài khoản Twitter chính thức:https://x.com/TechFlowPost
Tài khoản Twitter tiếng Anh:https://x.com/BlockFlow_News
















