
Paradigm最新研究:予測市場専用の統一自動マーケットメーカー「pm-AMM」
TechFlow厳選深潮セレクト

Paradigm最新研究:予測市場専用の統一自動マーケットメーカー「pm-AMM」
AMMおよびその前身(例:市場スコアリングルール)は、当初、予測市場に流動性を提供する手段として考案された。
執筆:Ciamac Moallemi、Dan Robinson、Paradigm
翻訳:Yangz、Techub News
概要
本稿では、予測市場に特化した新たな自動マーケットメイカー(AMM)である「pm-AMM」を紹介する。
AMM およびその前身である市場スコアリングルールは、当初、予測市場に流動性を提供する手段として考案された。現在では、これらは大部分のDEX取引高を支配している。しかし皮肉なことに、予測市場の取引高が急増しているにもかかわらず、その多くは依然としてオーダーブック方式を用いており、AMM はあまり使われていない。
その一因として、既存の AMM が「結果トークン」(事象が発生すれば1ドル、発生しなければ0ドルの価値を持つトークン)に適していないことが挙げられる。結果トークンのボラティリティは、事象の現在確率と予測市場の満期までの時間に依存するため、プールが提供する流動性は一貫しない。また、予測市場が満期を迎えると、流動性提供者(LP)は実質的にすべての価値を失うことになる。
そこで我々は、こうした点を考慮して最適化された新しいAMMを提案する。これは、AMM研究における長年の課題——特定の資産タイプに応じてAMMを最適化することの意味——に答えるものでもある。すなわち、ある資産(オプション、債券、ステーブルコイン、結果トークンなど)のモデルが与えられたとき、それがAMM設計にどのように影響するのか? 我々は「損失対リバランス(LVR)」という概念に基づき、この問いに対する一つの答えを提示する。
研究成果
我々は結果トークンの価格変動モデルを構築し、「ガウススコアダイナミクス(Gaussian score dynamics)」と呼ぶ。このモデルは、バスケットボールの得点差、選挙での票差、あるいは特定資産価格などの基本的ランダムプロセスが、将来の満期時にある閾値を超えるかどうかを予測する予測市場に適用可能である。
このモデルをもとに、結果トークン向けの新たな不変式ベースAMM——静的 pm-AMM 不変式——を導出する:
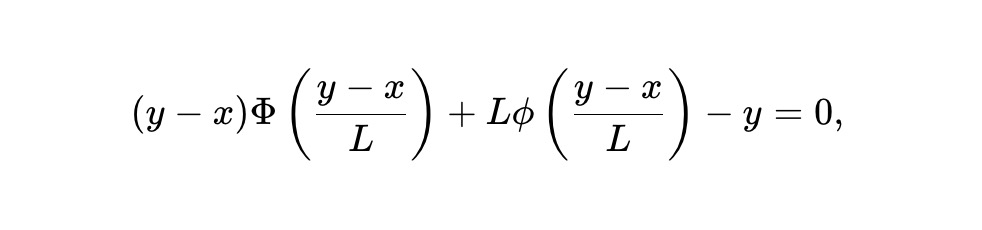
ここで、x は結果トークンのAMM内準備高、y はその反対・補完的な結果トークンの準備高、L は総流動性またはスケーリング係数、ϕ および Φ はそれぞれ標準正規分布の確率密度関数と累積分布関数を表す。
上記の不変式は、「損失対リバランス(LVR)」という強力な概念に基づく。LVRとは、裁定取引によりAMMが被る損失率を指し、AMMの形状および取引される資産の価格ダイナミクスに依存する。
ある資産に対して「均一AMM(uniform AMM)」とは、その資産に使用された場合、現在価格に関わらず常にLVRがその時点のポートフォリオ価値に対して一定の割合となるようなAMMを意味する。Milionisらの研究によれば、価格が幾何ブラウン運動(GBM)に従う資産(株式や暗号資産など)に対しては、恒常的幾何平均AMM(UniswapやBalancerなど)が唯一の均一AMMとなる。一方で、我々が提案する結果トークンのガウススコアダイナミクスに従う資産に対しては、静的 pm-AMM が均一AMMとなる。
静的 pm-AMM はすべての価格において均一なLVR(投資組合価値に対する割合)を持つが、予測市場の満期が近づくにつれてLVRは増加する。これは満期直前における予測市場の極端な不安定性による。これを緩和し、満期までの残り期間において期待LVRが常に一定となるようにするため、我々は満期までの時間 T-t に依存する動的 pm-AMM 不変式を導出する:
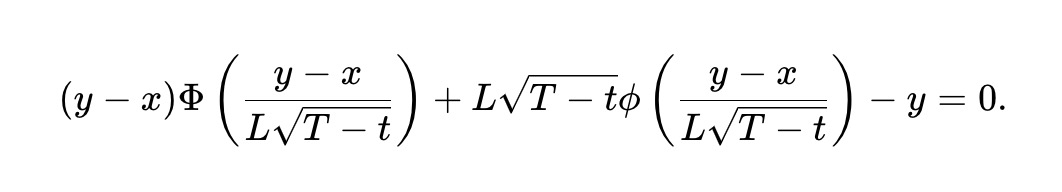
動的 pm-AMM は流動性を徐々に削減することで、満期に近づくほど増大するLVRを防ぐ。ただし、実際のプールでは非裁定取引活動(およびそれによって生じる手数料)も時間とともに増加する可能性があるため、流動性の継続的削減は必ずしも望ましいとは限らない。しかしpm-AMMは、LPが予想手数料や裁定リスクの配分方法に応じて流動性を調整するフレームワークを提供する。
これらのAMMは、オンチェーン予測市場への受動的流動性供給を促進する可能性がある。また、均一AMMの概念および関連手法は、ステーブルコイン、債券、オプションその他のデリバティブなど、幾何ブラウン運動に従わない価格ダイナミクスを持つ資産に対しても広く応用可能であり、DEX設計者にとって有用な設計指針となり得る。
図1は、静的および動的pm-AMMの不変曲線を、恒常的積AMM(CPMM)および対数市場スコアリングルール(LMSR)と比較したものである。動的pm-AMMは、時間の経過とともに提供する流動性が低くなることに注意されたい。
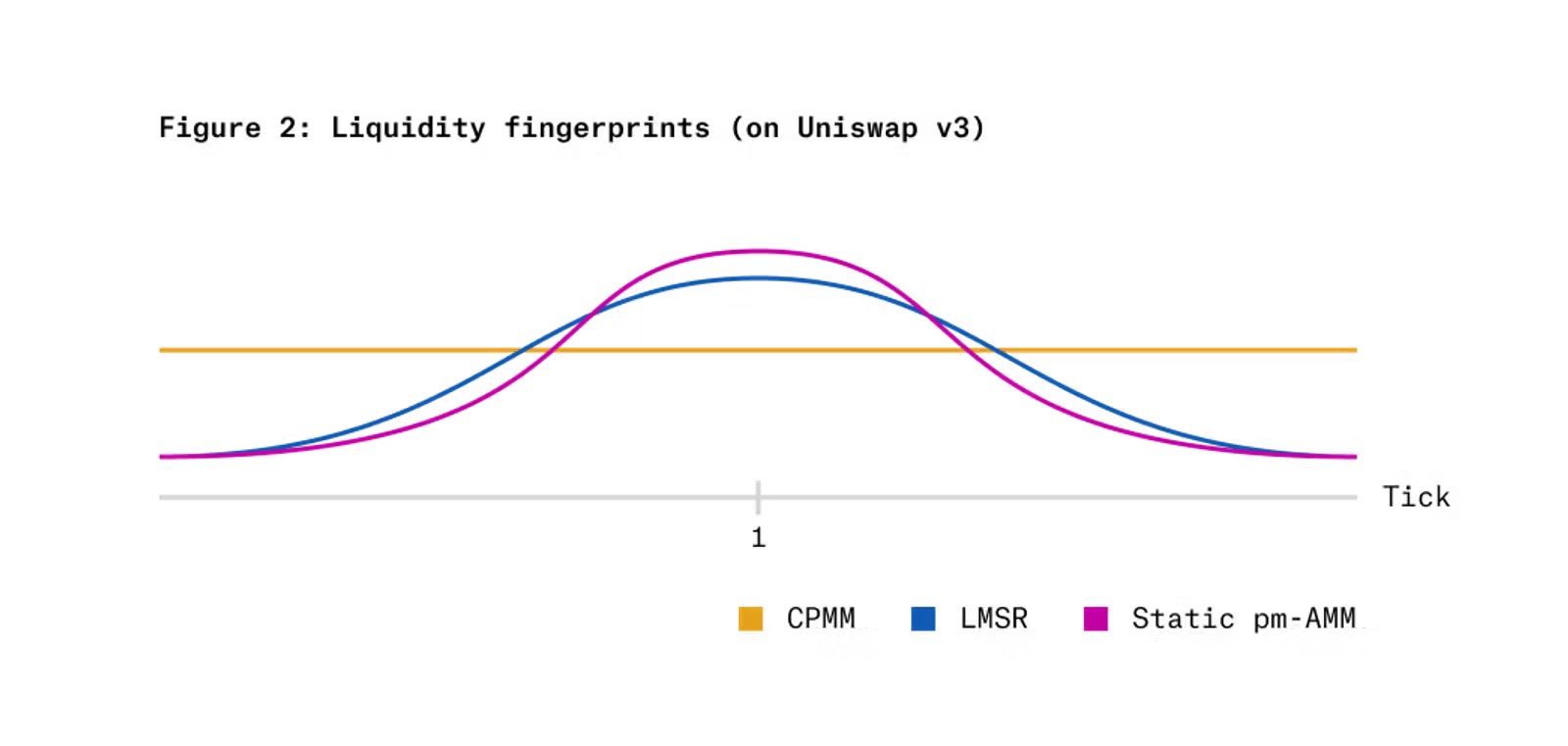
図2は、Uniswap v3の集中流動性AMM上に静的pm-AMM不変式を実装した場合の「流動性フィンガープリント(liquidity fingerprint)」を、CPMMおよびLMSRと比較したものである。横軸は相対価格(xトークン価格/yトークン価格)の対数スケール、縦軸は各AMMがその価格帯で提供する流動性を示す。pm-AMMは、相対価格が1(確率50%、つまりトークン価格0.50)付近に流動性を集中させ、極端な相対価格(非常に低いか高い)ではより少ない流動性しか提供しないことがわかる。
研究背景
予測市場
予測市場は、暗号資産分野においてますます人気のあるアプリケーションとなっている。2024年10月だけでも、Polymarketの取引高は20億ドルを超えている。しかし、多くの暗号資産ベースの予測市場では、主流のDEX取引の大半を占めるAMMではなく、オーダーブック方式で流動性が提供されている。
その理由の一つは、結果トークンの価格行動が通常の資産と異なるため、従来のAMMが安定して機能しないことにある。たとえば、1001回のコイントスを行うゲームに関する予測市場を考えよう。表が出たらxトークンが1ドル、裏が出たらyトークンが1ドルの価値を持つとする。最終的に表の回数が多ければxが1ドル、少なければ0ドルとなり、yは逆となる。
このような結果トークンのボラティリティは、残りのトス回数と現在のスコアに大きく依存する。現在のスコアが拮抗しており、残り回数が少ないほど、ボラティリティは高くなる。つまり、恒常的積AMMの損失(後述のようにボラティリティに依存)は時間とともに大きく変動する。
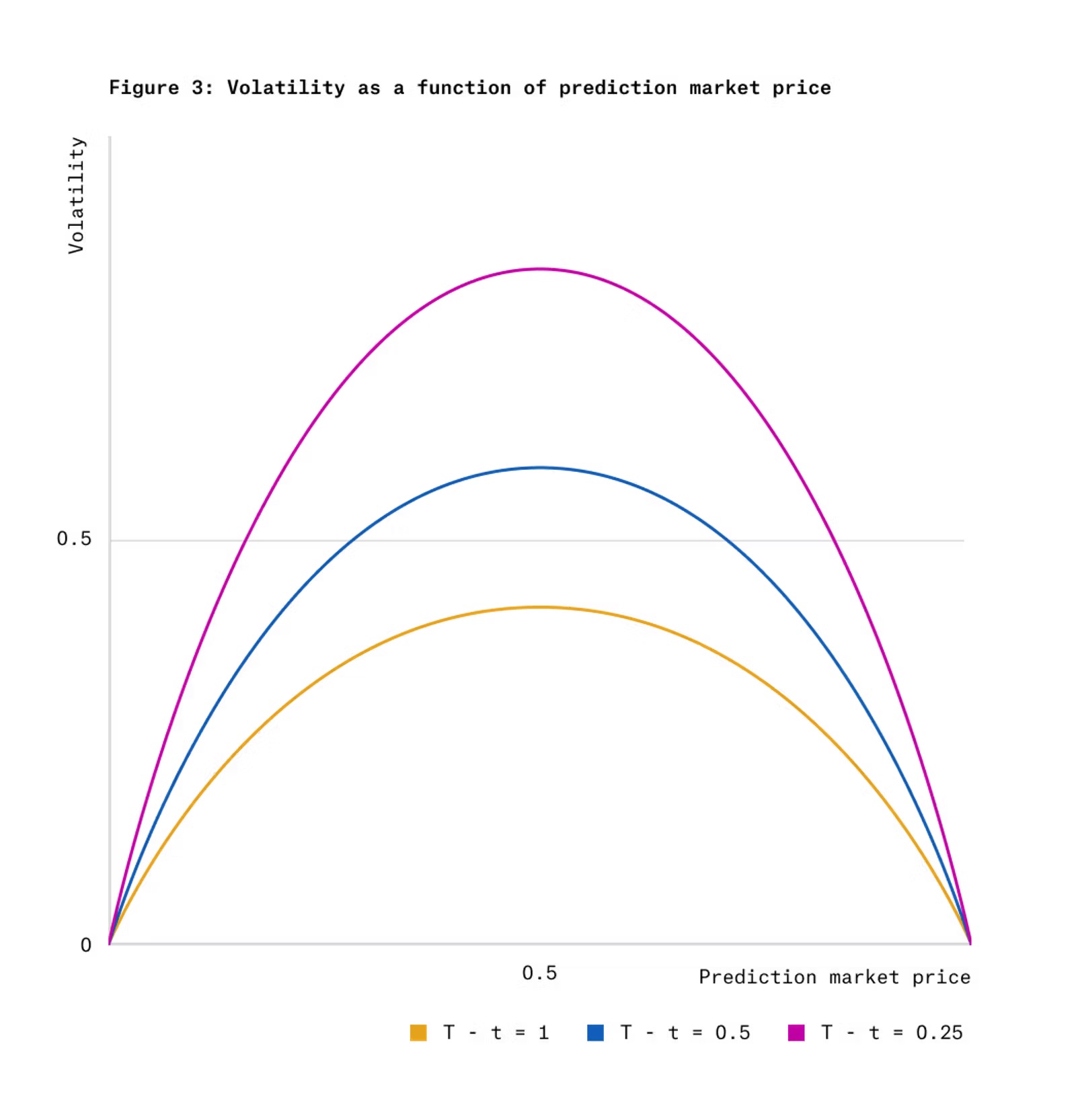
図3は、ガウススコアダイナミクス下における結果トークン価格のボラティリティが、価格および残り時間の関数としてどのように変化するかを示している。
多くの人気ある予測市場は、このコイントス例と類似しており、あるランダム過程が満期時に0より上か下かを賭けるものである。例えば:
-
バスケットボールの試合結果に関する予測市場は、試合終了時に満期を迎える。ランダム過程は両チーム間の得点差である。
-
大統領選挙の結果に関する予測市場は選挙日に満期を迎える。ランダム過程は候補者への投票意図者の人数差である。
-
ビットコインなどの資産価格が将来の日付においてある行使価格を超えるかを問う予測市場では、ランダム過程は現行価格から行使価格を引いた対数値となる。
本稿で定義する結果トークンの価格ダイナミクスモデル、すなわち「ガウススコアダイナミクス」は、こうした例から着想を得ている。このモデルは、予測市場価格が、ある潜在的ブラウン運動が0以上で終わる確率に一致すると仮定する。このモデルはバイナリオプションのBlack-Scholesモデルと類似している(バイナリオプションは、資産価格が行使価格を超えていれば固定金額を払い、そうでなければ0を支払う金融商品)。ただし、我々のモデルでは、潜在的プロセスが取引可能な資産価格に対応する必要はない。
我々は、結果トークンの価格が「1ドルとなる確率」と一致するという単純化された仮定をしている。これはリスクや時間選好といった市場の重要な側面を無視しており、これらがモデルにどう影響するかは今後の研究課題となる。
さらに、すべての予測市場がガウススコアダイナミクスに適合するわけではない。このモデルは新情報の出現速度が予測可能であることを前提としているため、得点頻度が高いバスケットボールはこのモデルに合いやすいが、得点が稀なサッカーには向かないかもしれない。また、地震のような一度限りの突発的イベントが特定日までに発生するかを予測する市場など、まったく異なるタイプの予測市場もある。とはいえ、本モデルは他のダイナミクスを導出するための有用な出発点となり得る。また、任意のモデルに対して均一AMMを導出する方法の実例としても機能する。
損失対リバランスと均一性
このモデルを明確にした上で、結果トークンに既存のAMM(恒常的積AMMやLMSRなど)よりも適したメカニズムを導出する。その指標として用いるのは、流動性提供者の期待損失率、すなわち「損失対リバランス(loss-vs-rebalancing, LVR)」である。
LVRはAMMの主な逆選択コストを捉えるものであり、取引がない場合、AMMの価格は静的であり、新たな情報が入ると価格が陳腐化してしまうことに起因する。この陳腐化した価格を利用し、情報に優る裁定者が不利な価格で取引することで、LPは損失を被る。このため、LVRはAMMが価格修正のために裁定者に支払っている費用とみなせる。
また、取引手数料がない場合、LVRはLPが保有するポジションを、AMMプール内のトークン数量と同一の空売りヘッジ(デルタヘッジ)によって完全にリスク除去した場合の損失とも一致する。この点で、LVRはBlack-Scholesオプション価格理論の核心的洞察に基づいている。オプションが原資産とのデルタヘッジを通じて市場リスクを排除するように、LVRも市場リスクを除去した上でAMM内LPポジションの価値を評価する。つまり、LVRは単にAMM準備高と同じトークンを保有する市場リスクとは別に、AMM内で流動性提供者としての特殊リスクを隔離するものである。
ここでは、手数料やMEV回収メカニズムを持たない単純な不変式ベースAMMを想定する。この場合、AMMは裁定取引により必然的に損失を被る。どのような不変式を用いてもLVRを完全に排除することはできない(取引自体を発生させない不変式を除く)。また、LVRを「最小化」すること自体にも実用的な意味はなく、それは単に提供する流動性を減らすことに等しい。
しかし、LVRを「均一化」することは可能であり、これにより損失されるプール価値の割合が、資産の現在価格に依存しなくなる。この性質を我々は「均一性(uniformity)」と呼ぶ。
あるスポンサーが、あるゼロ手数料の予測市場に流動性を提供し、結果の市場予測を知ろうとしているとしよう。このスポンサーは損失を被るが、特定の時期や価格帯に損失が集中するより、損失を均等に分散させたいと考えるだろう。この場合、プールの現在の投資組合価値はスポンサーの「予算」と見なせる。均一AMMでは、ある時点で1ドルの流動性を投入した場合、次の時点での期待損失はプールの現在状態に依存しない。
さらに、利益を追求するLPにとっても均一性には潜在的な意義がある。たとえAMMがLVRからの損失を一部回収したり(非ゼロのスワップ手数料やMEV税によるオークションなど)、黒字化できたとしても、異なる価格帯や時間帯にどう流動性を配分するかの戦略が必要となる。ゼロ手数料プールの期待損失は、資産の価格過程を考慮した上で、特定の時点でどれだけの流動性を配置すべきかを判断する指標と見なせる。
我々は、ある特定資産について、その現在価格にかかわらず期待LVRがプールの現在価値に対して一定の割合となるAMMを「均一AMM」と定義する。なお、AMMが均一LVRを持つかどうかは、資産そのものの価格過程に依存する。Milionisらの付録B.2によれば、資産価格が幾何ブラウン運動に従う場合、その資産に対する実質的に唯一の均一AMMは加重幾何平均AMMであり、その不変式は以下の通りである:
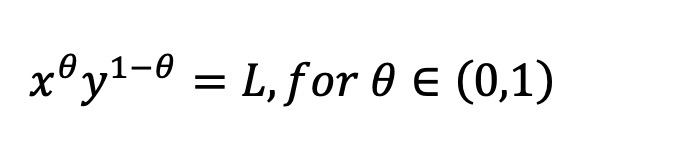
これはBalancerで使用される式であり、Uniswap v2の恒常的積AMMもその特殊ケースである。しかし、ガウススコアダイナミクスに従うトークンに対しては、恒常的幾何平均AMMもLMSRも均一LVRを持たない。
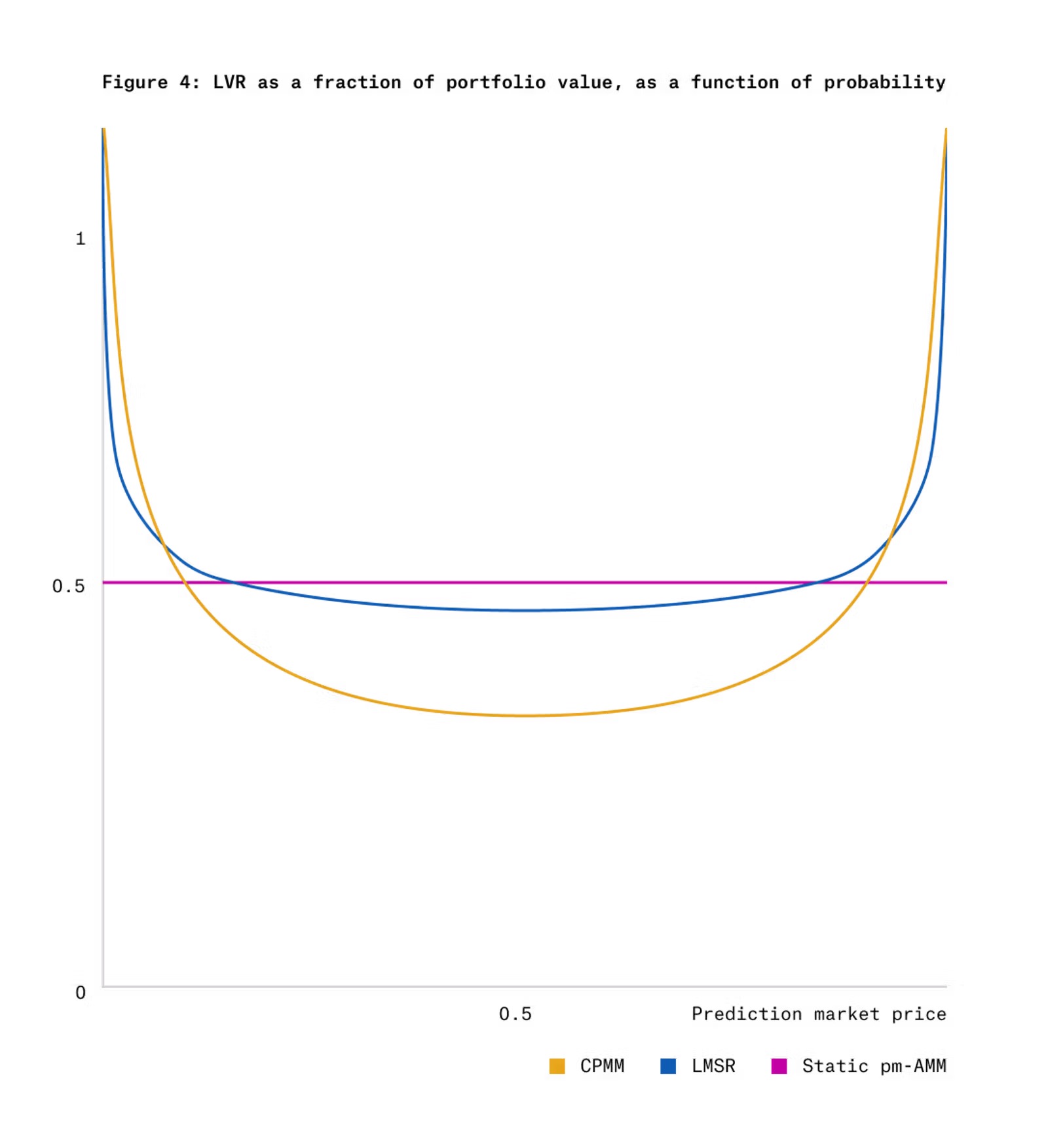
図4は、時間 T-t=1 の時点で、ガウススコアダイナミクスに従う結果トークンに対して、CPMMおよびLMSRと静的pm-AMMのLVRを比較したものである。
以上の考察から、我々はガウススコアダイナミクス下の予測市場向けに2種類のAMMを開発した。1つは任意の時点で均一なLVRを持つが、満期に近づくにつれてLVRが増加する静的pm-AMM。もう1つは残り期間を通じて均一なLVRと一定の期待LVRを持つ動的pm-AMMである。
図4から、結果トークン価格が0または1に極端に近いとき、CPMMおよびLMSRは大きなLVRを示すことがわかる。これは、これらの領域では価格のボラティリティが低い(図3参照)にもかかわらず、極端価格ではプール価値の減衰が速くなるためである。したがって、均一AMMは極端価格でより少ない流動性を提供すべきであり、まさにこれがpm-AMMの設計が目指すところである(図2参照)。
先行研究
AMMの起源は予測市場および市場スコアリングルール(LMSRなど)にある。これらは恒常関数マーケットメイカー(CFMM)の発見を促し、Uniswap v2のような、AMMが各資産の準備高間に不変関係を持つことを特徴とする設計へとつながった。こうしたAMMは近年、DEXの主流な市場メカニズムとなっている。
最近では、金融経済学の視点がAMMのコスト理解に応用され、特に幾何ブラウン運動を前提とした「損失対リバランス(LVR)」の概念が中心となっている。一方、予測市場の価格ダイナミクスは、有限の利得と期限を持つ点で大きく異なる。Talebは潜在的可観測な投票プロセスに基づくダイナミクスを提唱したが、我々は潜在的可観測なガウススコアプロセスに基づく別のダイナミクスを構築した。
GBM以外の資産向けAMM設計については、すでにいくつかの応用研究がある。例の一つがStableSwapであり、ステーブルコインペア向けのAMMで、関連資産が平均回帰的であるという直感に基づき、流動性を特定価格付近に集中させる。しかし、その導出には資産価格過程のモデリングは含まれていない。もう一つの例はYieldSpaceであり、ゼロクーポン債向けのAMMである。YieldSpaceの導出には単純なゼロクーポン債価格モデルが含まれるが、金利の変動プロセスまではモデル化していない。
さらに、資産価格行動に関する信念に基づくリアルタイム市場モデルの設計に関する学術的研究もある。Goyalらの研究が代表的である。彼らの枠組みは「期待アクティブ流動性の最大化」を目指しており、期待損失の一様化とは異なる。そのため、時には我々と逆の結論に至る。例えば、彼らはLPが相対価格が1付近に留まると予想する場合、LMSR(CPMMに比べて価格1付近に流動性を集中)が適していると導く。一方、我々の枠組みでは、価格分化が予想される場合(結果トークンなど)にこそ、価格1付近に流動性を集中的に配置する理由があると考える。
各種AMMモデル
自動マーケットメイカー
単一事象に関する予測市場と、2つの対立する資産を取引するAMMを考える。リスク資産xは事象が発生すれば1ドルを支払い、そうでなければ0;リスク資産yはその逆とする。AMMは不変式 f(x,y)=L を維持する。ここで f(・,・) は準備高 (x,y) の不変関数、L は定数である。x資産の価格P(米ドル単位)が与えられたとき、プールの価値関数は以下で与えられる:
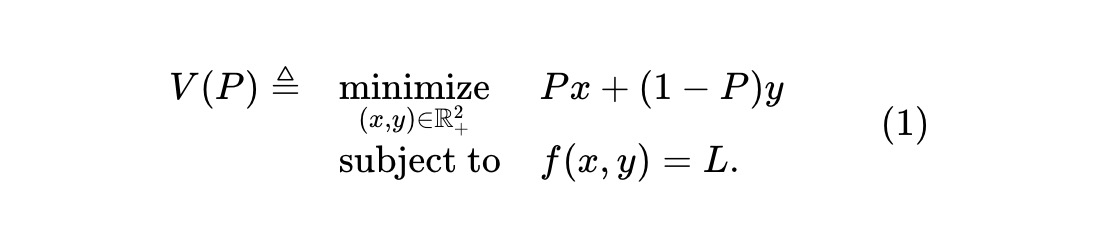
これは価格Pにおけるプールの価値である。1単位のxとyを同時に持つことは現金1ドルと等価であるため、yの価格は1-Pでなければならない。各時点tで、裁定者はx資産の価格Pt(およびyの価格1-Pt)を観測できると仮定する。取引手数料やその他の摩擦がない場合、裁定者は常にAMMを監視し、誤価格から利益を得ようとする。自己利益を最大化する中で、彼らはAMMの準備価値を最小化するように取引を行う。Vtを時点t(価格Pt)における準備価値とすれば、Vt = V(Pt) である。
例1:恒常的積AMM(CPMM)の場合、不変式は f(x,y)≜xy であり、プール価値関数は:
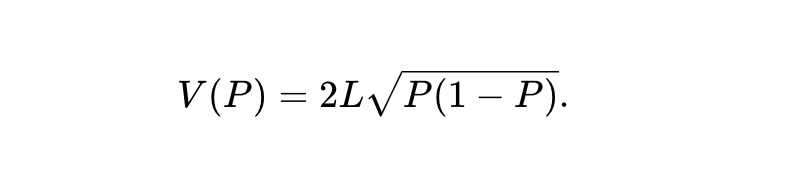
例2:Robin Hansonが開発した対数市場スコアリングルール(LMSR)は、以下の不変式を満たすAMMと見なせる。
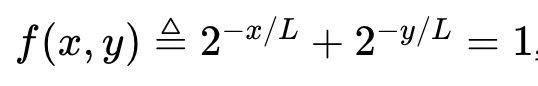
そのプール価値関数は(価格が暗示する事象の二項エントロピーに比例):
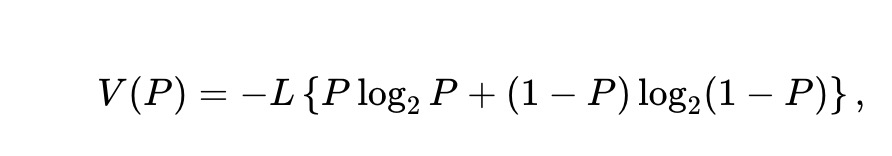
x*(P) および y*(P) を最適化問題(1)の最適解とし、それらが存在し、一意であり、価格Pに関して十分滑らかであると仮定する。このとき、以下の定理はMilionisらの定理1と類似しているが、本稿の文脈に適合している:
定理1. すべての価格 P≥0 に対して、プール価値関数は以下を満たす:
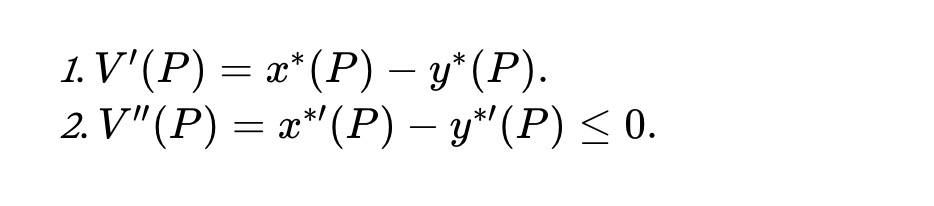
ガウススコアダイナミクス
リスク資産価格は、我々が「ガウススコアダイナミクス」と呼ぶ過程に従ってどのように時間発展するか? 具体的には、時間区間 t∈[0,T] 上でランダム過程 {Zt} が存在し、事象は Zt が時刻 T で終了する際の符号によって決まる:ZT≥0 ならx資産が償還、ZT<0 ならy資産が償還。Zt は両者の競争における得点差と解釈でき、ここでは「スコアプロセス」と呼ぶ。なお、モデルはこのスコアプロセスの存在を仮定するが、AMMがそれを直接観測する必要はない。後述するように、AMMは限界価格(裁定後)と満期時間からスコアの現在値を推定できる。
Zt はランダムに変動すると仮定する。具体的には、Zt がボラティリティ σ>0 のブラウン運動に従う、すなわち dZt=σdBt(Bt は標準ブラウン運動)と仮定する。このとき、x資産の時点tにおける価格 Pt は:
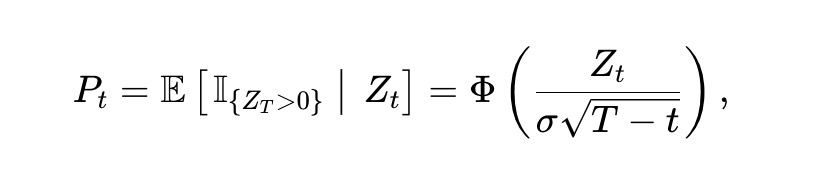
ここで、Φ(・) は標準正規累積分布関数(CDF)である。伊藤の定理を適用すれば、Pt は次を満たす:
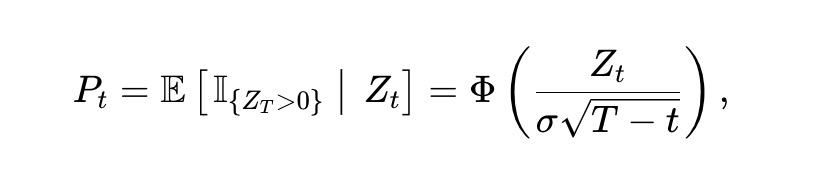
ここで、ϕ(・) は標準正規確率密度関数、Φ⁻¹(・) は逆CDFである。スコアダイナミクスおよびスコアから価格への変換はσに依存するが、孤立した価格過程 Pt のダイナミクスはσに依存しないことに注意。このダイナミクスのボラティリティと価格・残り時間の関係は図3に示す。
均一AMM
前述の議論より、Vt を時点tにおけるプール準備価値(価格Pt)とすれば、Vt=V(Pt) である。伊藤の定理を適用すれば、プール価値の変化は以下で与えられる:
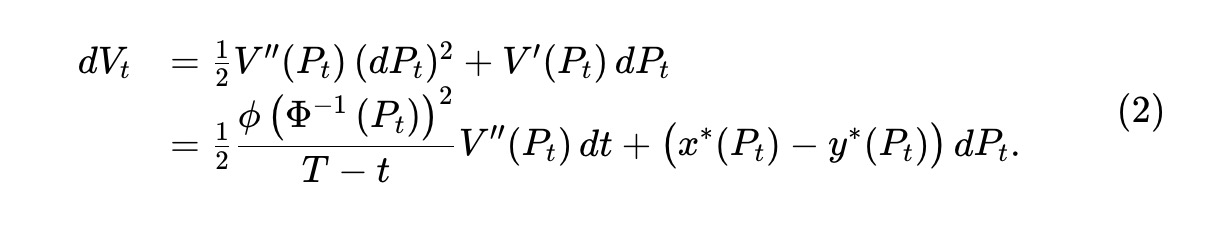
Pt がマルチンゲールであるため、(2)の第2項もマルチンゲール(増加または減少)となる。一方、V(・)(定理1参照)に基づく第1項は負の変換に対応し、従って減少過程となる。これがMilionisらが提唱する「損失対リバランス」プロセスであり、不利な価格でプールと取引する裁定者によって失われる価値を捉える。この損失の瞬時レートを以下で定義する:
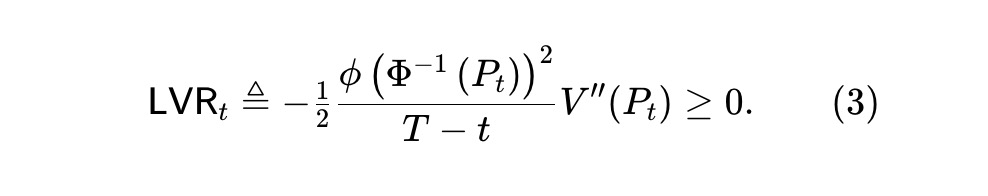
Milionisらは、幾何ブラウン運動に従う資産に対しては、実質的に幾何平均AMMのみが均一AMMであることを示した。ガウススコアダイナミクス下の予測市場では、(3)を検討するため、均一LVRプールは以下の常微分方程式(ODE)を解かねばならない:
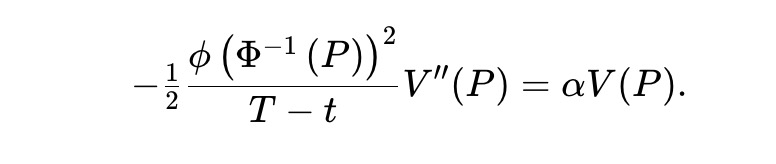
これは不可能である。なぜなら左辺はtに依存し、右辺はtに依存しないためである。根本的な問題は、幾何ブラウン運動が時間不変であるのに対し、ガウススコアダイナミクスは時間に強く依存していることにある。
この問題を回避するため、αを時間依存とし、α=β/(T-t)(β>0)と設定する。すなわち、以下の設定を考える:
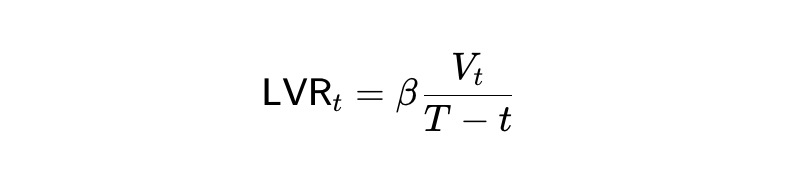
これは P≥0 におけるODEと等価である。さらに、V(・)にはV''(P)≤0 などの追加条件が必要である(定理1参照)。
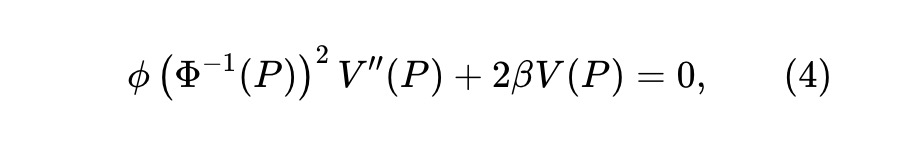
静的 pm-AMM
変数変換 u=Φ⁻¹(P) を行うことで上記ODEを簡略化できる。β=1/2 のとき、ODEおよび追加の凹性条件を満たす解が存在し:
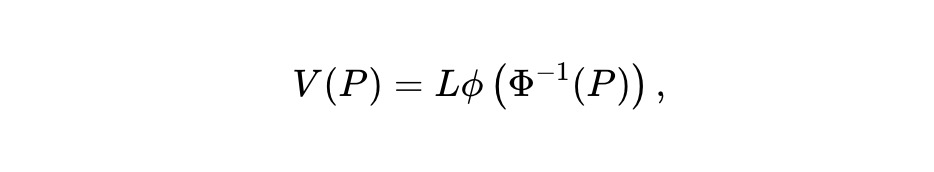
xおよびyトークンの準備高は:
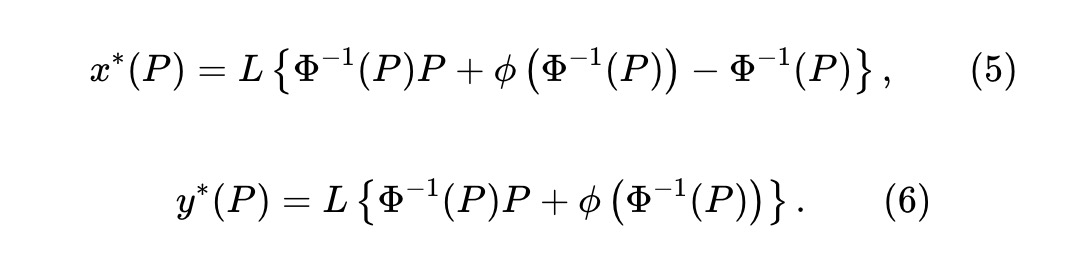
ここで、L≥0 は流動性パラメータであり、プール規模のスケーリングを決定する。y*(P)−x*(P)=LΦ⁻¹(P) を(5)に代入すると、プール準備高 (x,y) は以下の不変式を満たさねばならない:
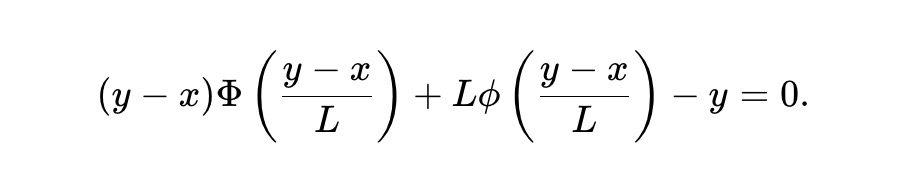
これが静的 pm-AMM の定義である。設計上、このAMMは以下を満たす:
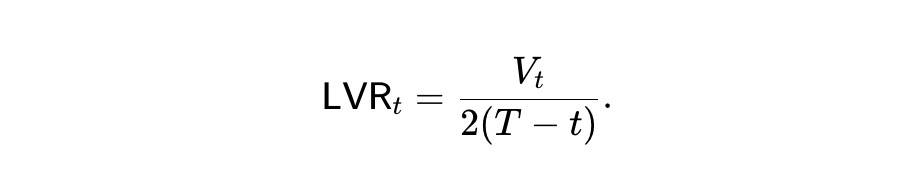
V̄t=E[Vt] を期待プール価値と定義すると、(2)より:
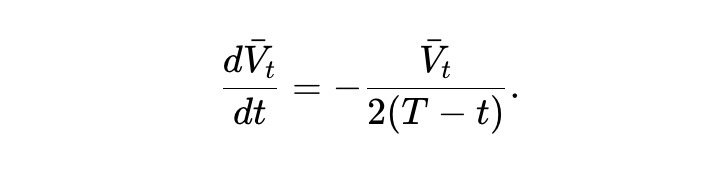
この常微分方程式を解くことで、以下の結果が得られる。つまり、期待値としては、静的 pm-AMM のプール価値は残り期間の平方根に比例して減衰する。
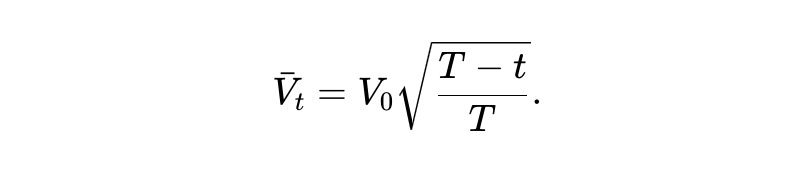
動的 pm-AMM
静的 pm-AMM の欠点は、すべての価格において1ドルあたりのLVRが均一であるものの、時間とともに変化することにある。特に、1ドルあたりの損失は満期までの時間に反比例するため、時間とともに増加し、満期時にはすべての価値を失う。
動的流動性。我々は、静的 pm-AMM の設計を時間変化させる動的版を想定する。すなわち、AMMのLPが時間とともに流動性を引き出すことで損失を抑える。具体的には、プール価値が以下で与えられると仮定する:
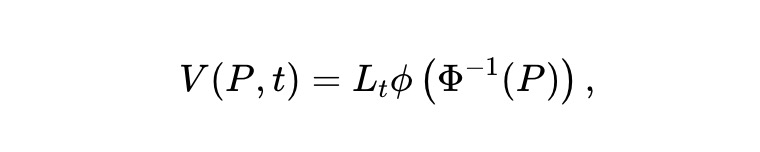
ここで、Lt は時間とともに流動性が取り出される(あるいは追加される)程度を決める決定論的で滑らかな関数である。伊藤の定理をプール価値過程 Vt≜V(Pt,t) に適用すると:
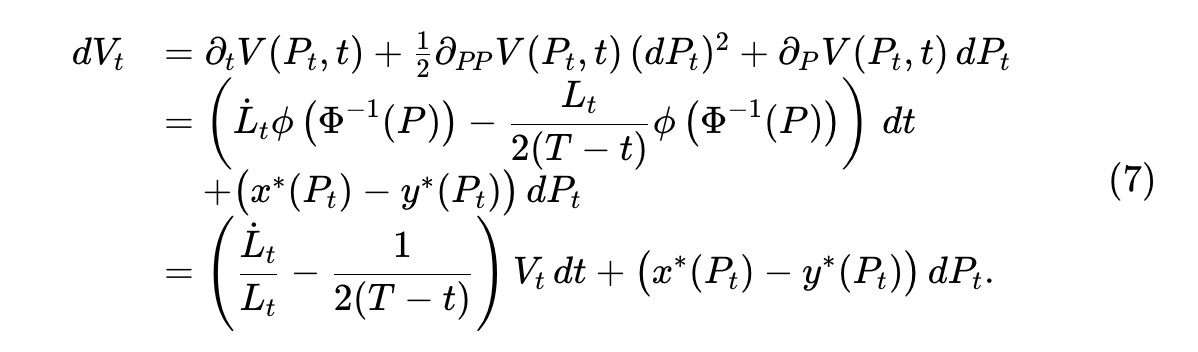
Ct を引き出された流動性の累計ドル価値とする。プール価値は流動性 Lt に線形に依存するため、Lt 変化のドル価値は Vt/LT に比例する。よって:
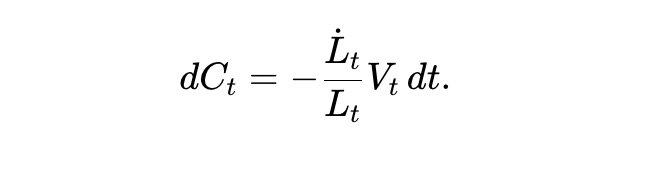
AMM LPの総財産 Wt はプール準備価値と引き出し累計価値の和であり、Wt=Vt+Ct で、以下を満たす:
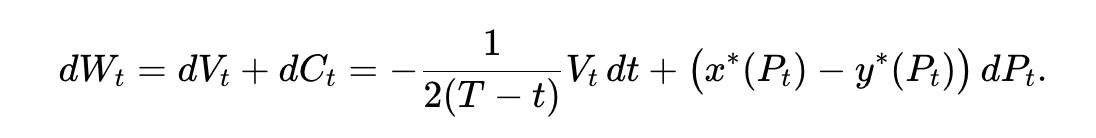
したがって、LPの期待財産 W̄t≜E[Wt] は以下を満たす。ここで V̄t≜E[VT] とする。
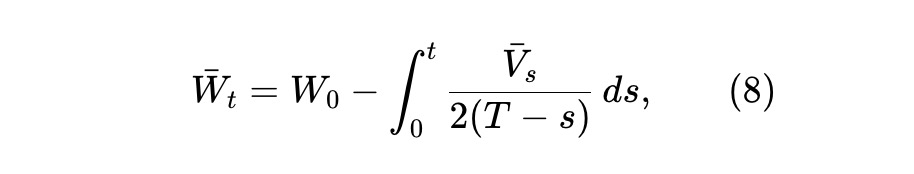
ここで、以下の流動性曲線を選択する:
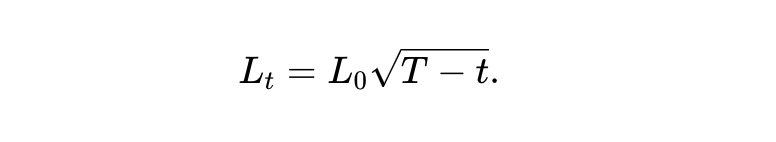
これを「動的 pm-AMM」と呼ぶ。(7)より、期待プール価値 V̄t=E[Vt] は:
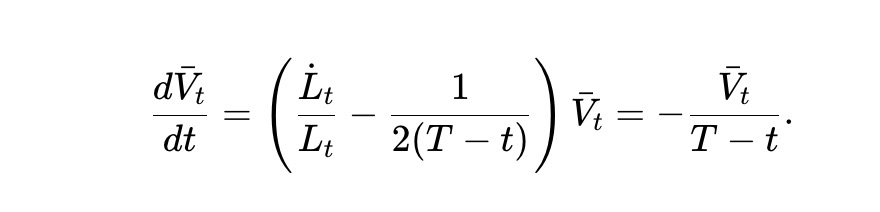
この常微分方程式を解くことで、以下の結果が得られる。
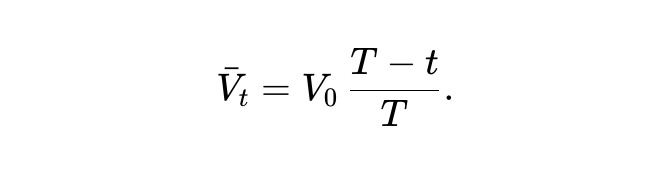
つまり、動的 pm-AMM では、引き出しを差し引いた後、期待プール価値は線形に減少する。また、静的 pm-AMM の価値関数を継承しているため、単位時間あたりのLVR損失率は:
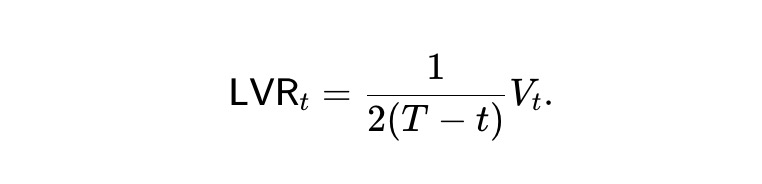
期待損失率は以下の値で、期間 t を通じて一定となる。つまり、時間とともに動的 pm-AMM は(期待値として)一定の速度で裁定者に資金を失う。
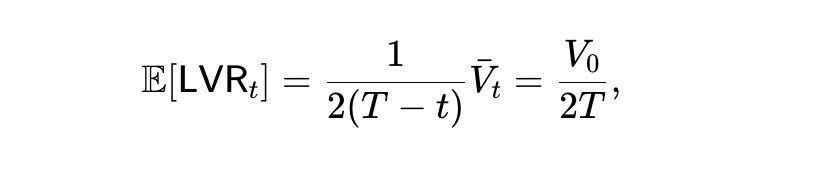
最後に、(8)より期待財産過程は下図のようになる。したがって、初期財産の半分が最終的に失われる。
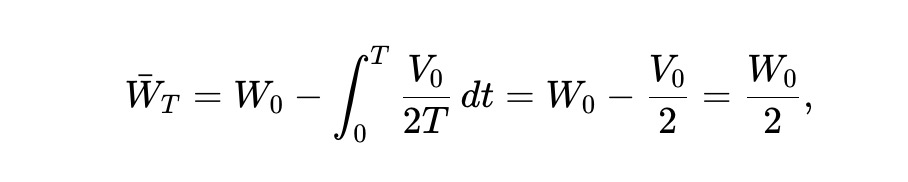
結論
pm-AMM は、ガウススコアダイナミクスモデルなどのダイナミクスで駆動される予測市場に適している可能性がある。さらに、本研究は、債券、オプション、その他のデリバティブなど、他の資産タイプに対しても均一AMMが適用可能であることを示唆している。
TechFlow公式コミュニティへようこそ
Telegram購読グループ:https://t.me/TechFlowDaily
Twitter公式アカウント:https://x.com/TechFlowPost
Twitter英語アカウント:https://x.com/BlockFlow_News
















