
多因子戦略による強力な暗号資産投資ポートフォリオ構築の理論的基礎
TechFlow厳選深潮セレクト

多因子戦略による強力な暗号資産投資ポートフォリオ構築の理論的基礎
「ファクター」とは、テクニカル分析における「指標」、人工知能の機械学習における「特徴量」であり、暗号資産のリターンの上下を決定する要因のこと。
序論
昨年6月に、多要因モデルを用いた仮想通貨選定の簡単な構想を示しました。
1年後、我々は暗号資産市場向けの多要因戦略の開発に着手し、その全体的な戦略フレームワークを『多要因戦略で強力な暗号資産ポートフォリオを構築する』というシリーズ記事としてまとめました。
本シリーズの概要(微調整の可能性あり)は以下の通りです:
一、多要因モデルの理論的基礎
二、単一要因の構築
-
要因データの前処理
-
データの選別
-
外れ値処理:極端値、誤り値、欠損値
-
標準化
-
中立化:業種、市場、時価総額
-
-
要因の有効性評価
- 情報比率(IC)、収益率、シャープレシオ、回転率
三、主要要因の合成
-
要因間の多重共線性分析
-
直交化による要因間多重共線性の排除
-
古典的加重法→合成要因
-
等加重、ローリングIC加重、IC_IR加重
-
合成要因のテスト:収益率、グループ別収益率、要因値加重収益率、合成要因IC、グループ別回転率
-
-
その他の加重法(要因と収益率が非線形関係にある場合):機械学習、強化学習(暗号通貨業界の特殊性から考慮しない)
四、リスク最適化ポートフォリオ
以下は第一編「理論基礎編」の本文内容です。
一、「要因」とは何か
「要因」とは、テクニカル分析における「指標」や、AI機械学習における「特徴量(フィーチャー)」であり、暗号通貨の収益率の上下を決定する要因である。
当チームは、暗号通貨分野でよく見られる要因タイプを、ファンダメンタル要因、オンチェーン要因、価格・出来高要因、デリバティブ要因、代替要因、マクロ要因に分類しています。
「要因」を発掘・計算する最終目的は、資産の期待収益率を正確に算出することにある。
二、「要因」の計算
(1)多要因モデルの導出
起源:単一要因モデル――CAPM
要因研究の歴史は20世紀60年代に遡る。資本資産価格モデル(Capital Asset Pricing Model, CAPM)が登場し、リスクが企業の資本コストに与える影響を通じて期待収益率を定量化した。CAPM理論によれば、個別資産の期待超過収益率は以下の単回帰モデルによって決定される。
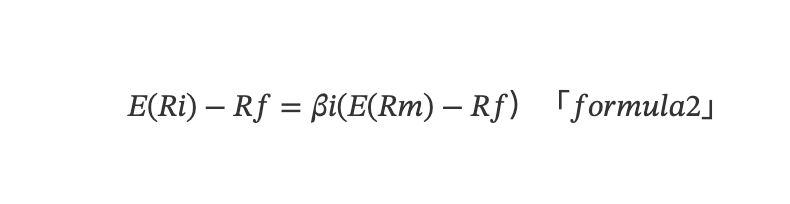
E(Ri) は数学的期待値、Ri は資産の収益率、Rfは無リスク収益率、Rmは市場ポートフォリオの収益率、βi = Cov(Ri,Rm)/Var(Rm) は資産収益率の市場収益率に対する感応度を示し、資産が市場リスクに対してどれだけ露出しているかを表す。
補足説明:
-
金融市場において、「リスク」と「リターン」は本質的に同種のものである。
-
βi の統計学的詳細理解
CAPMは切片項なしの二変数回帰モデル Yi = β1 + β2 · X (β1 = 0) と見なせ、通常の最小二乗法(OLS)によりモデルパラメータの推定値を得る。ここでβ1 = β2 = Σ(X-μX)(Y-μY)/ Σ(X-μX)² = Cov(X,Y)/Var(X) となる。
β1 は説明変数(市場収益率)が1単位変動したとき、被説明変数(資産iの収益率)が平均してどの程度変動するかを示す。金融分野ではこの変動度をYがXに対して「感応する」または「露出する」度合いと解釈する。
β>1 市場変動を拡大
β = 1 市場変動と完全に一致
0<β<1 市場と同方向に変動するが、市場より変動幅が小さい
β≤ 0 市場と逆方向に変動
1. 金融学におけるリスクとリターンの観点からのβiの詳細理解
投資ポートフォリオには2種類のリスクがある。システムリスク(市場リスク、分散不能リスク)と非システムリスク(分散可能リスク)。βi はシステムリスクであり、いかなるポートフォリオ構築を行っても、このリスクは固有であり、除去できない。以下に述べるαiは非システムリスクであり、異なる戦略構築によってヘッジすることが可能である。
CAPMモデルは最も単純な線形要因モデルであり、資産の超過収益が市場ポートフォリオ(市場要因)の期待超過収益と資産の市場リスクへの露出度のみによって決まると主張する。このモデルはその後の多くの線形多要因価格付けモデル研究の理論的基礎を築いた。
発展:多要因モデル――APT
CAPMの基盤の上、人々は異なる資産の収益率が複数の要因に影響されることを発見し、裁定価格理論(Arbitrage Pricing Theory, APT)が登場し、線形多要因モデルを構築した。
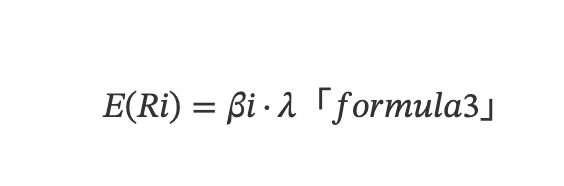
ここで、E(Ri)は資産iの期待収益、λは要因の期待収益(要因プレミアム)を表す。式(2)では、CAPMモデルのE(Ri) - Rfの代わりにE(Ri)を使って期待収益を表現している。これは、裁定取引により構成された資金中立投資ポジションでは、Rfが相殺され、資産全体の期待収益率はロングとショートの期待収益率の差になるため、E(Ri)を使った方が一般的である。
成熟:多要因モデル――アルファ収益とベータ収益
金融市場における実際の価格付け誤差とAPTモデルを総合的に考慮し、時系列の観点から、個別資産の期待収益率は以下の多元線形モデルによって決定される。
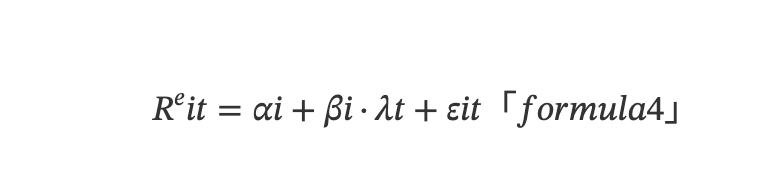
ここで、Rᵉit は時点tにおける資産iの収益、λt は時点tにおける要因収益率(要因プレミアム)、εit は時点tにおけるランダムノイズ。αi は資産iの実際の期待収益率と多要因モデルが暗示する期待収益率との価格付け誤差を表し、統計的にゼロから有意に逸脱すれば、それは超過収益を得るチャンスを意味する。βi = Cov(Ri,λ)/Var(λ) は資産iの要因露出度または要因ロードを表し、資産収益が要因収益に対してどれだけ感応するかを示す。
多要因モデルは資産の期待収益率の断面的差異に注目するものであり、本質的には平均に関するモデルである。期待収益率とは時間軸上の収益率の平均である。式(3)に基づき、断面的視点からの多元線形モデルを導出できる。
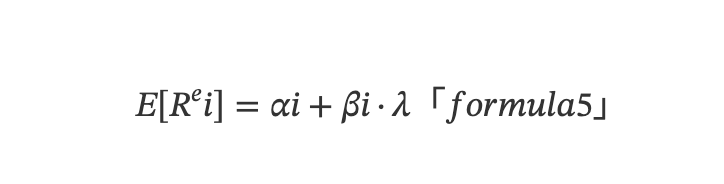
ここで、E[Rᵉi] は資産iの期待超過収益を表し、εit を時系列上で平均すると E(εit)=0 となる。
補足説明:
学術的視点から、市場効率性理論によれば、効率的な資産ポートフォリオは分散可能なリスクが完全にゼロであるべきであり、実際の収益率は期待収益率に等しく、期待資産収益率は市場のシステマティックリスクのみに依存する、つまり E[Rᵉi] = βi · λ であり、超過収益(Abnormal Return, AR)は存在せず、AR = Ri - E(Rᵉi) = 0 となる。しかし現実の金融世界は通常、市場が非効率的であり、超過収益が存在する、すなわち AR = α となる。
投資ポートフォリオがN個の資産から構成され、各資産iに対応する要因収益λを異なる要因に分解すると、以下の多要因モデルによるポートフォリオ収益率が得られる。
Rp = ∑ᴺᵢ₌₁Wi(αi+∑ᴹⱼ₌₁βᵢⱼfᵢⱼ)
ここで、Rp はポートフォリオの超過収益、Wiは各資産のポートフォリオ内ウェイト、βijは各資産の各要因におけるリスク露出度、λ = ∑ᴹⱼ₌₁βᵢⱼfᵢⱼ、fᵢⱼ は各資産の各要因ごとの単位要因ロードあたりの要因収益率である。
統計学の知識を組み合わせると、このモデルは以下の3つの仮定を内包している。
-
各資産のベータ収益とアルファ収益は無相関:Cov(αi,βiλ)=0
-
異なる資産間の特有収益率も無相関:Cov(αi,αj)=0
-
要因は必ず資産収益率に関連している:Cov(Rᵉi,βiλ)≠0
ベータ収益とアルファ収益の統合的解釈:
具体的な金融市場と結びつけると、βiλ は市場全体のパフォーマンスに属するベータ収益であり、αi は資産自身の特性によって生じるアルファ収益、すなわち市場をどれだけ上回るかを示す。各資産の収益率はベータ収益とアルファ収益から構成されており、人々は多要因モデルにおける各資産のαi値を利用して各資産にスコアをつけたり重みづけたりすることでポートフォリオを構築でき、先物を用いてベータ収益部分を売却ヘッジすることでリスクを相殺し、アルファ収益を得ることができる。
(2)多要因モデルのボラティリティ
ポートフォリオを構築する際には、リスクとリターンのバランスを取る必要があり、上記モデルを制約付き最適化問題として定式化して解くことになる。ポートフォリオのリスク、すなわちポートフォリオのボラティリティ σ²p について、以下にその導出を行う。ポートフォリオ構築の詳細分析は「リスク最適化ポートフォリオ」の章で述べる。
式(3)の行列表現 Rp = W(β ∧ + α) より、ポートフォリオのボラティリティは次のように表せる。
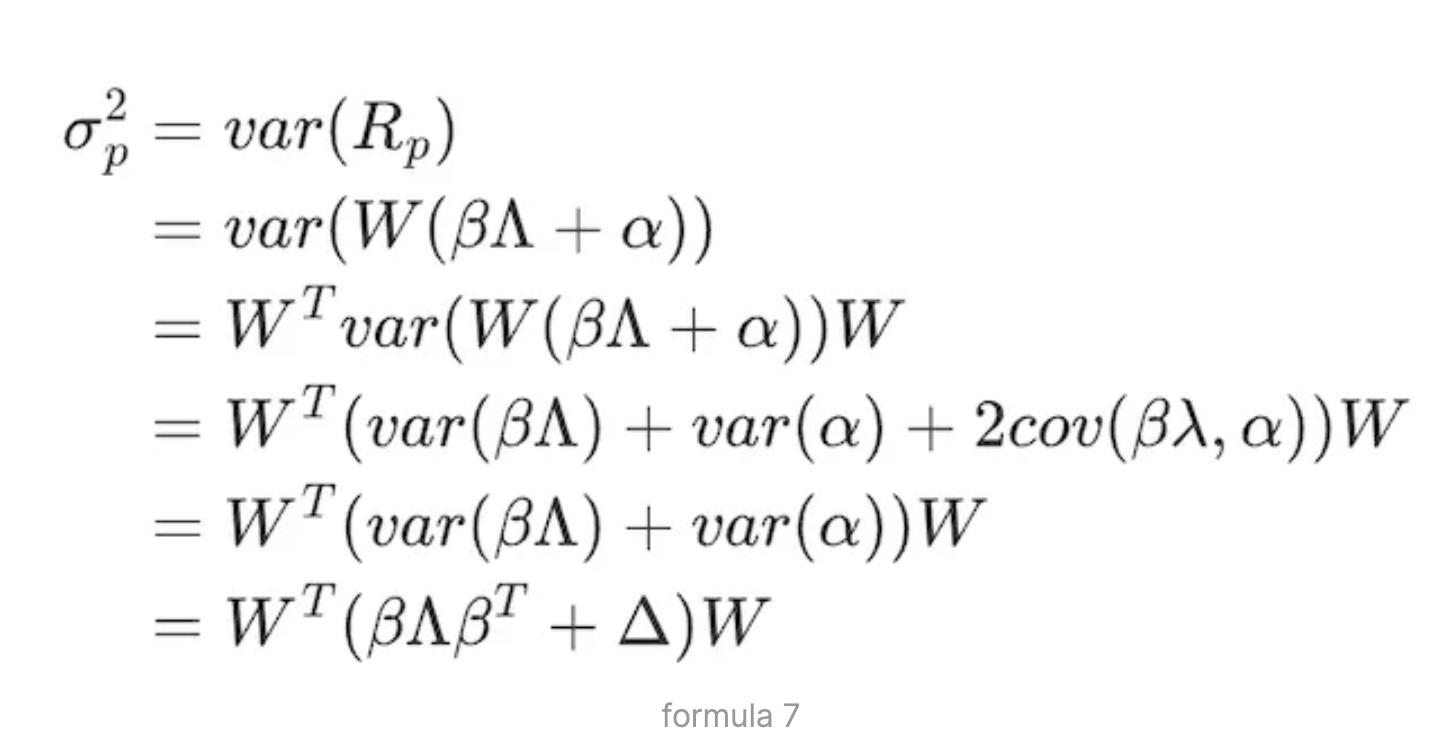
ここで、Wは資産の重み行列、βは要因の重み行列であり、N個の資産がK個のリスク要因に対して持つ要因ロード行列(N×K)を表す。

∧ はK個の要因の要因収益率の共分散行列(K×K)を表す。

仮定3より、異なる資産間の特有収益率も無相関であることから、Δ 行列は以下のようになる。

TechFlow公式コミュニティへようこそ
Telegram購読グループ:https://t.me/TechFlowDaily
Twitter公式アカウント:https://x.com/TechFlowPost
Twitter英語アカウント:https://x.com/BlockFlow_News















