
Paradigm最新 recherche : un market maker automatisé unifié dédié aux marchés prédictifs, le pm-AMM
TechFlow SélectionTechFlow Sélection

Paradigm最新 recherche : un market maker automatisé unifié dédié aux marchés prédictifs, le pm-AMM
Les AMM et leurs prédécesseurs (comme les règles de notation du marché) ont été initialement inventés comme moyen de fournir de la liquidité aux marchés prédictifs.
Rédaction : Ciamac Moallemi, Dan Robinson, Paradigm
Traduction : Yangz, Techub News
Introduction
Dans cet article, nous présentons un nouveau type de market-maker automatique (AMM) spécialement conçu pour les marchés prédictifs : le pm-AMM.
Les AMM et leurs prédécesseurs (comme les règles de notation des marchés) ont été initialement inventés comme moyen de fournir de la liquidité aux marchés prédictifs. Aujourd'hui, ils dominent une grande partie du volume des échanges sur les DEX. Ironiquement, toutefois, malgré une hausse spectaculaire du volume des marchés prédictifs, la plupart d'entre eux utilisent des carnets d'ordres plutôt que des AMM.
Une explication possible est que les AMM existants ne conviennent pas bien aux jetons-résultats (c’est-à-dire des jetons valant 1 $ si un événement se produit, 0 $ sinon). La volatilité des jetons-résultats dépend de la probabilité actuelle de l’événement et du temps restant avant l’expiration du marché prédictif, ce qui rend la liquidité fournie par les pools incohérente. Une fois le marché prédictif arrivé à échéance, les fournisseurs de liquidité (LP) perdent essentiellement toute leur valeur.
C’est pourquoi nous proposons un nouveau type d’AMM optimisé précisément autour de ces contraintes, répondant ainsi à une question ouverte en recherche AMM : que signifie optimiser un AMM pour un type d’actif spécifique ? Autrement dit, étant donné un modèle d’un actif (options, obligations, stablecoins ou jetons-résultats), comment cela devrait-il influencer notre conception d’un AMM ? Nous proposons une réponse fondée sur le concept de « Loss vs Rebalancing » (LVR).
Résultats
Nous modélisons la dynamique des prix de certains jetons-résultats, que nous appelons « dynamique gaussienne du score ». Ce modèle s'applique à des marchés prédictifs où l'on cherche à anticiper si un processus aléatoire sous-jacent (l'écart de points dans un match de basket, l'écart de voix dans une élection ou le prix d'un actif) dépassera un seuil donné à une date d'échéance future.
À partir de ce modèle, nous dérivons une nouvelle famille d’AMM basés sur une invariante, appelée invariante pm-AMM statique :
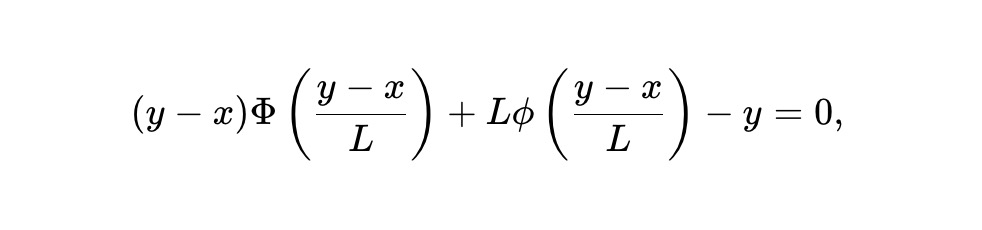
Où x est la réserve du jeton-résultat dans l’AMM, y celle du jeton complémentaire, L est la liquidité totale ou coefficient de proportionnalité, ϕ et Φ sont respectivement la fonction de densité et la fonction de répartition de la loi normale.
Cette invariante repose sur un concept puissant : la perte face au rééquilibrage (LVR), mesurant le taux de perte d’un AMM dû à l’arbitrage. Le LVR dépend à la fois de la forme de l’AMM et de la dynamique des prix de l’actif négocié.
Nous définissons un AMM uniforme pour un actif donné comme un AMM dont le LVR, exprimé en pourcentage de la valeur du portefeuille, est constant quel que soit le prix courant. Milionis et al. ont montré que pour un actif dont le prix suit un mouvement brownien géométrique (GBM — un modèle populaire pour les actions ou cryptomonnaies), le seul AMM uniforme est celui à moyenne géométrique constante (comme Uniswap ou Balancer). Le pm-AMM statique est l’unique AMM uniforme pour les actifs suivant notre modèle de dynamique gaussienne du score.
Bien que le pm-AMM statique ait un LVR uniforme à tout prix, ce dernier augmente néanmoins avec l’approche de l’échéance, car les marchés prédictifs deviennent très volatils près de l’expiration. Pour ajuster le pm-AMM afin de réduire sa liquidité progressivement, et maintenir un LVR espéré constant à chaque instant avant l’échéance, nous dérivons l’invariante du pm-AMM dynamique, qui dépend du temps restant T-t :
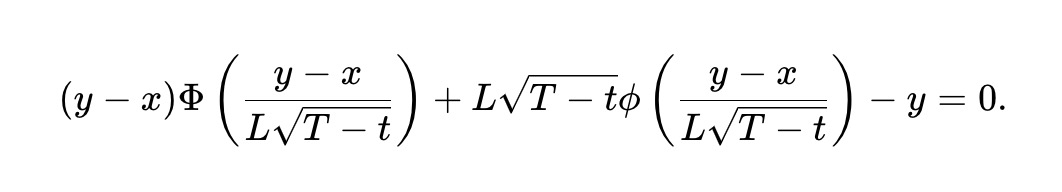
Le mécanisme du pm-AMM dynamique empêche l’augmentation du LVR en offrant une liquidité décroissante. Dans un pool réel, ceci peut ne pas être souhaitable, surtout si l’activité non arbitragiste (et donc les frais générés) augmente également avec le temps. Toutefois, le pm-AMM offre aux LP un cadre pour adapter leur liquidité selon les frais attendus et leur stratégie de gestion du risque d’arbitrage.
Ces AMM pourraient aider à mobiliser une liquidité passive sur les marchés prédictifs blockchain. Le concept d’AMM uniforme et la méthodologie associée pourraient aussi intéresser plus largement les concepteurs de DEX, en vue de concevoir des AMM adaptés à d’autres types d’actifs dont la dynamique ne suit pas un GBM, tels que les stablecoins, obligations, options ou autres produits dérivés.
La figure 1 compare les courbes invariantes du pm-AMM statique et dynamique avec celles du market-maker à produit constant (CPMM) et de la règle de notation logarithmique (LMSR). On observe que le pm-AMM dynamique offre moins de liquidité au fil du temps.
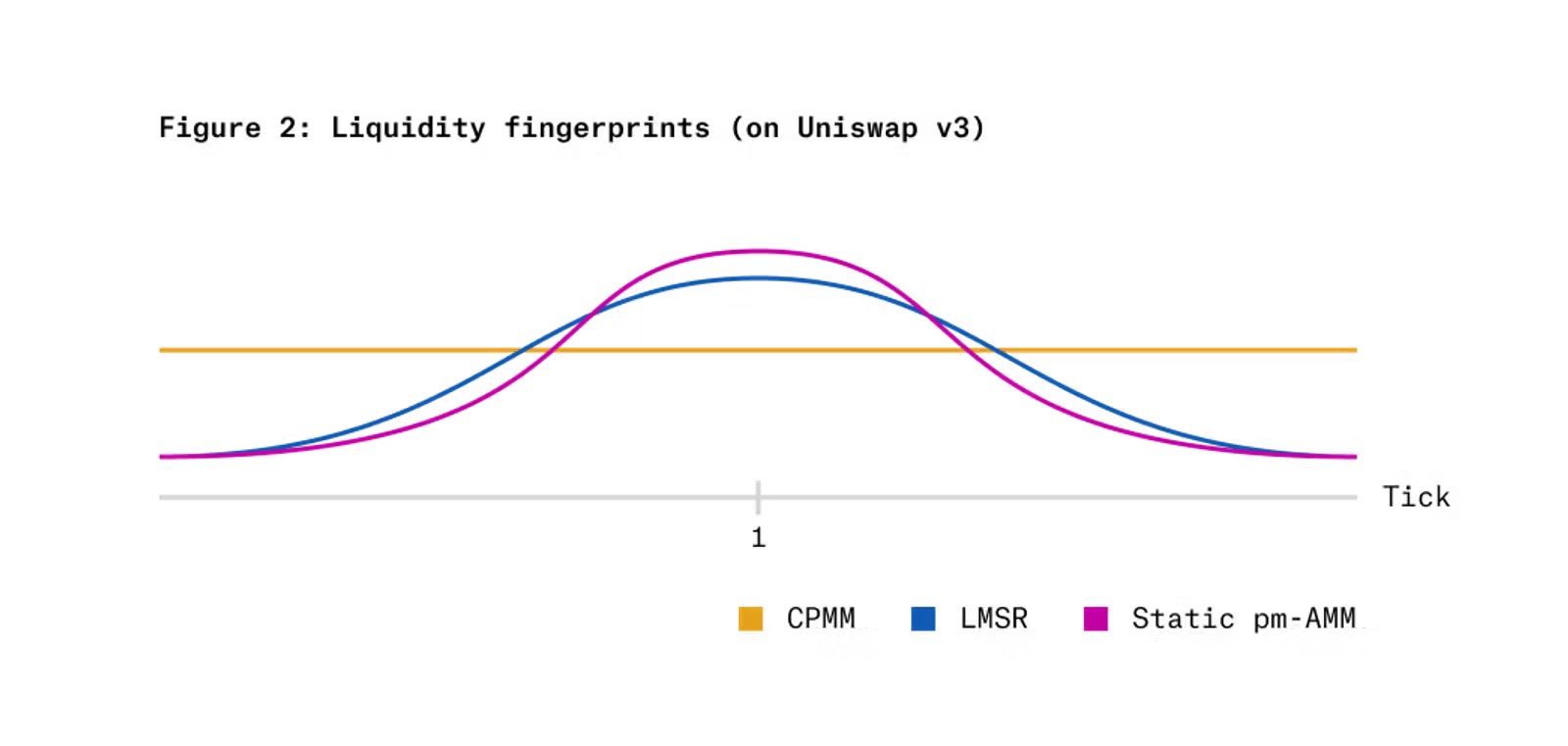
La figure 2 montre le « doigté de liquidité » (liquidity fingerprint) obtenu si l’invariante du pm-AMM statique était implémentée sur un AMM à liquidité concentrée comme Uniswap v3, comparé au CPMM et au LMSR. L’axe horizontal représente l’échelle logarithmique du prix relatif (prix du jeton x divisé par prix du jeton y), l’axe vertical la liquidité fournie par chaque AMM à ce niveau de prix. On observe que le pm-AMM concentre davantage de liquidité autour d’un prix relatif de 1 (probabilité de 50 %, prix des jetons à 0,50 $) et moins en prix extrêmes (très faibles ou très élevés), par rapport aux deux alternatives.
Contexte
Marchés prédictifs
Les marchés prédictifs gagnent en popularité dans l’écosystème crypto. En octobre 2024 seulement, Polymarket a dépassé 2 milliards de dollars de volume. Pourtant, la majorité de la liquidité sur ces marchés provient de carnets d’ordres, et non d’AMM, alors même que ces derniers dominent les volumes des DEX.
Une raison probable est que le comportement des prix des jetons-résultats diffère de celui des actifs traditionnels, rendant les AMM standard instables. Prenons un exemple simple : un marché prédictif sur un jeu de pile ou face, où l’on lance 1001 fois une pièce. Deux jetons, x et y, représentent respectivement pile et face. Si pile sort plus souvent, le jeton x vaut 1 $, sinon 0 $ ; inversement pour y.
La volatilité de ces jetons dépend fortement du nombre de lancers restants et de l’écart actuel. Plus l’écart est serré et le nombre de lancers faible, plus la volatilité est élevée. Par conséquent, la perte d’un AMM à produit constant (qui dépend de la volatilité, comme expliqué plus bas) varie considérablement dans le temps.
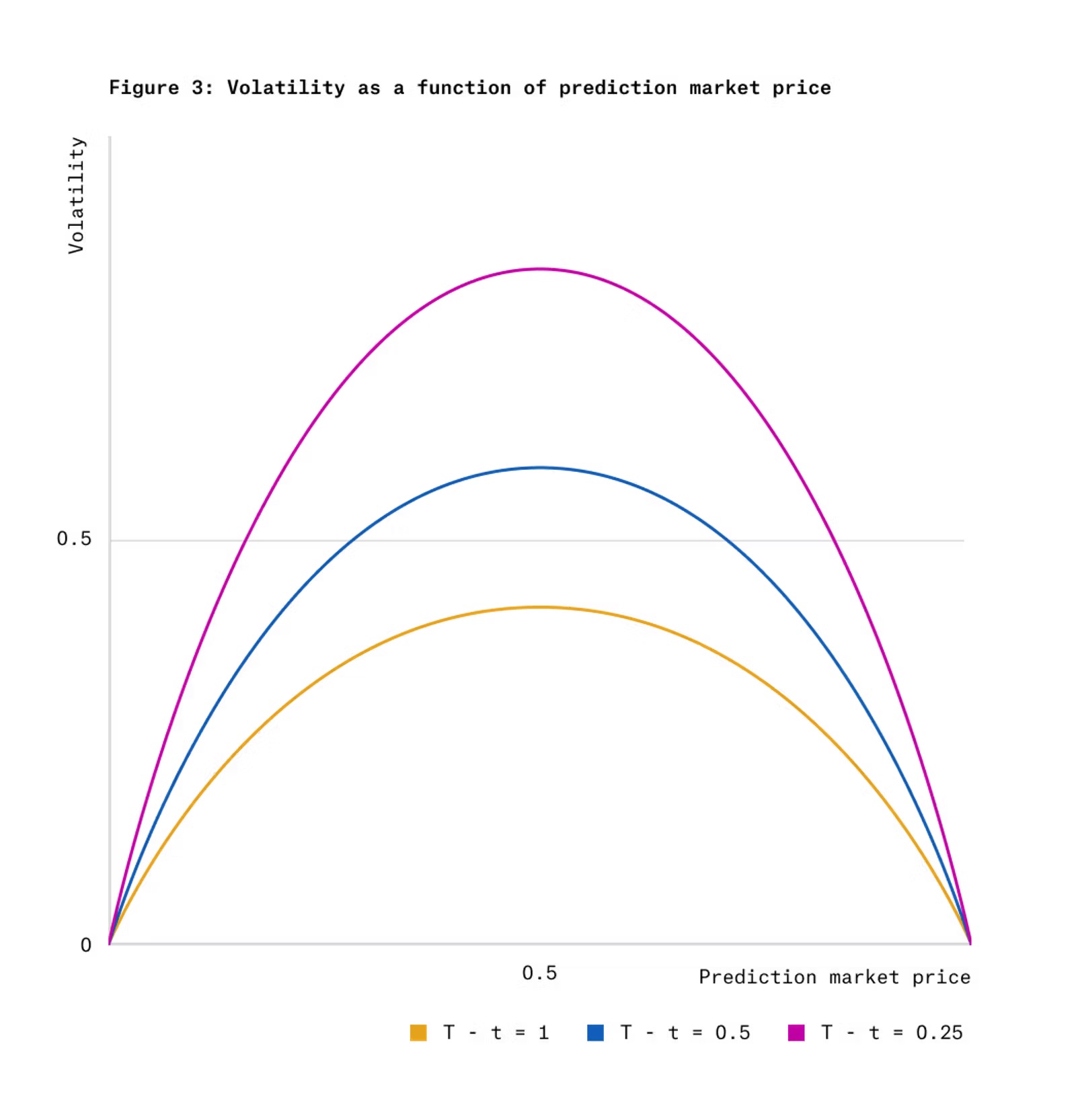
La figure 3 illustre la relation entre la volatilité du prix d’un jeton-résultat, son prix courant et le temps restant, sous la dynamique gaussienne du score.
De nombreux marchés prédictifs réels ressemblent à cet exemple, posant une question binaire sur la position d’un processus aléatoire à une échéance donnée :
-
Dans un marché sur un match de basket, le marché expire quand le temps atteint zéro. Le processus aléatoire est l’écart de points entre les deux équipes.
-
Un marché sur une élection présidentielle expire le jour du scrutin. Le processus est l’écart de votes entre candidats.
-
Un marché sur le prix du Bitcoin à une date future, par rapport à un prix d’exercice, peut modéliser le processus comme le logarithme du prix actuel moins le prix d’exercice.
Le modèle de dynamique gaussienne du score présenté ici s’inspire de ces exemples. Il suppose que le prix du marché prédictif correspond à la probabilité qu’un mouvement brownien sous-jacent termine au-dessus de zéro. Ce modèle rappelle le modèle Black-Scholes pour les options binaires (produits versant un montant fixe si le prix dépasse un seuil). Toutefois, dans notre cas, le processus sous-jacent n’a pas besoin d’être lié à un actif négociable.
Nous faisons une simplification : le prix du jeton-résultat égale exactement la probabilité qu’il paie 1 $. Cette hypothèse ignore des éléments importants comme la prime de risque ou la préférence temporelle, qui feront l’objet de recherches futures.
Par ailleurs, tous les marchés prédictifs ne conviennent pas à ce modèle, qui suppose un flux d’information régulier. Par exemple, un match de basket s’y prête mieux qu’un match de football, car les paniers sont plus fréquents, rendant l’évolution du score plus régulière. Certains marchés prédictifs, comme ceux sur un événement ponctuel (ex. séisme), ne correspondent pas du tout à ce modèle. Néanmoins, il constitue un point de départ utile pour d’autres dynamiques, et illustre la méthode pour dériver un AMM uniforme à partir d’un modèle donné.
Perte vs Rééquilibrage et Uniformité
Ayant défini ce modèle, nous dérivons un mécanisme potentiellement mieux adapté à ces jetons que les AMM existants (comme CPMM ou LMSR). Notre indicateur central est le taux de perte espéré des LP, formalisé comme « perte face au rééquilibrage » (LVR).
Le LVR capture le coût principal de sélection adverse pour un AMM : sans transactions, le prix de l’AMM stagne, devient obsolète face aux nouvelles informations, et est exploité par des arbitragistes mieux informés. Le LVR mesure donc le coût supporté par les LP, ou encore la rémunération versée aux arbitragistes pour remettre les prix à jour.
En l’absence de frais, le LVR correspond aussi à la perte subie par un LP qui couvre son exposition (hedging delta) en vendant à découvert la même quantité de jetons que dans le pool. Ainsi, le LVR s’appuie sur l’intuition centrale du modèle Black-Scholes : tout comme une option peut être couverte contre le risque de marché via un hedging delta, le LVR valorise la position LP après élimination du risque de marché. Il isole ainsi le coût spécifique d’être fournisseur de liquidité dans un AMM, distinct du simple risque de détention.
Nous étudions des AMM simples basés sur une invariante, sans frais ni récupération de MEV. Dans ce cadre, un AMM perdra toujours de l’argent à cause de l’arbitrage — aucune invariante ne peut annuler le LVR (sauf à supprimer totalement les échanges). De plus, « minimiser » le LVR n’a pas de sens pratique, car cela reviendrait simplement à réduire la liquidité offerte.
Toutefois, bien que le LVR ne puisse être éliminé, on peut le rendre plus uniforme : que la perte en pourcentage de la valeur du pool ne dépende pas du prix courant. Cette propriété s’appelle l’uniformité.
Imaginons un sponsor prêt à fournir de la liquidité sans frais sur un marché prédictif, juste pour observer les cotes du marché. Il perdra de l’argent, mais préférerait répartir cette perte uniformément dans le temps et les prix, plutôt que de la concentrer à certains moments. Dans ce cas, la valeur courante du pool est son « budget ». Sur un AMM uniforme, injecter 1 $ de liquidité à un instant donné entraîne une perte espérée identique au pas de temps suivant, quelle que soit l’état du pool.
L’uniformité présente aussi un intérêt potentiel pour les LP cherchant à maximiser leurs profits. Même si un AMM pouvait compenser ou inverser ses pertes (via des frais ou une taxe MEV), il aurait besoin d’une stratégie pour allouer sa liquidité dans le temps et les prix. Le LVR d’un pool sans frais peut alors servir d’indicateur pour guider cette allocation, en tenant compte du processus de prix de l’actif.
Nous définissons un AMM uniforme pour un actif donné comme un AMM dont le LVR espéré est une fraction constante de la valeur courante du pool, quel que soit le prix. Notons que l’uniformité dépend du processus de prix de l’actif. Comme montré par Milionis et al. (appendice B.2), si le prix suit un GBM, l’unique AMM uniforme est celui à moyenne géométrique pondérée, d’invariante :
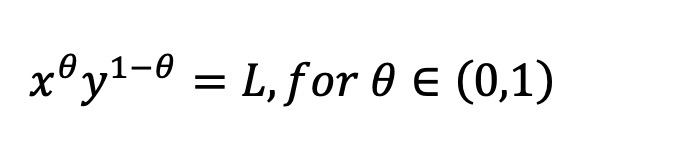
C’est la formule utilisée par Balancer, et le CPMM d’Uniswap v2 en est un cas particulier. Mais pour des jetons suivant une dynamique gaussienne du score, ni le CPMM ni la LMSR n’ont un LVR uniforme.
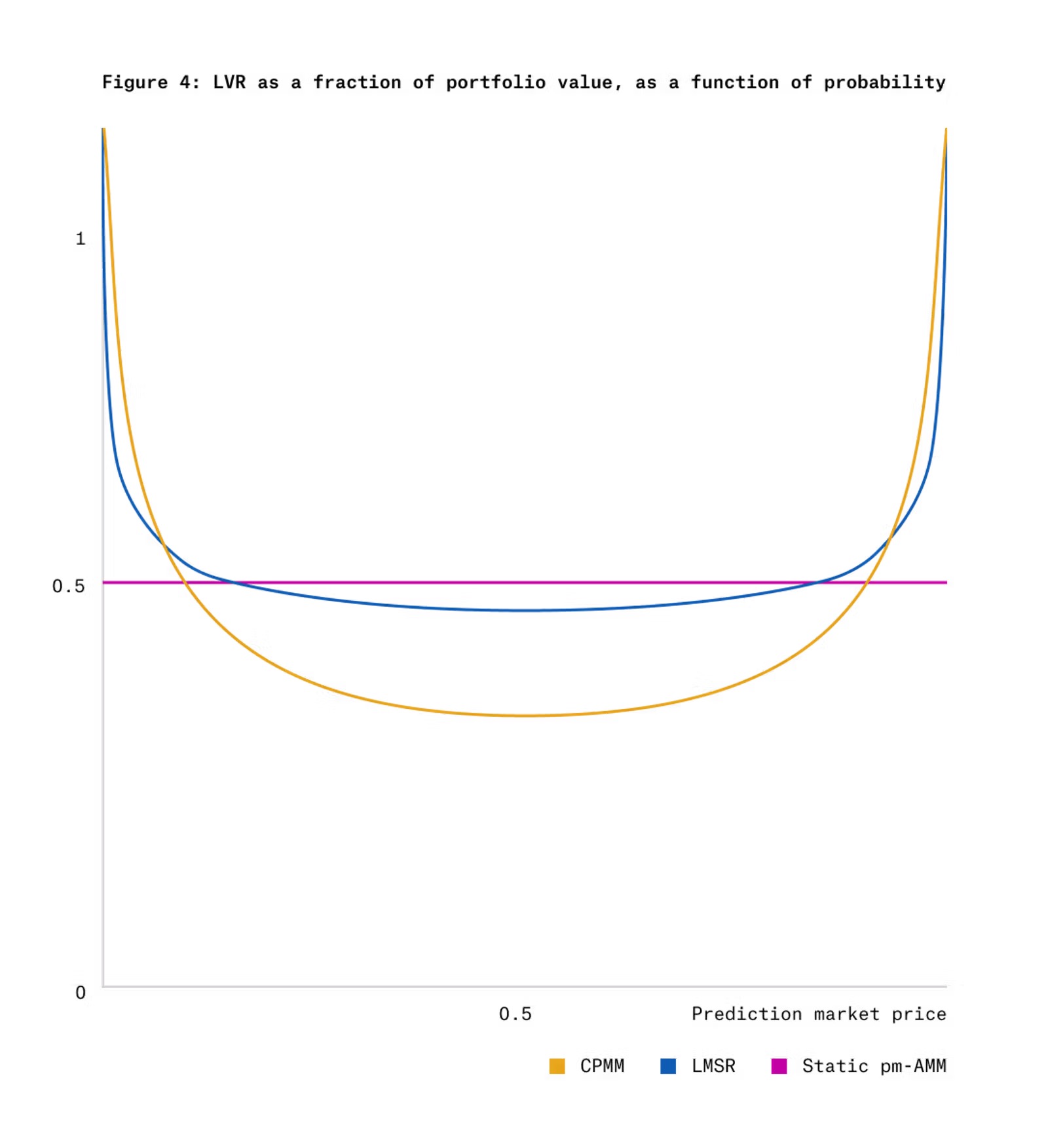
La figure 4 compare le LVR du CPMM et de la LMSR avec celui du pm-AMM statique (uniforme) pour des jetons-résultats sous dynamique gaussienne, à T-t=1.
Comme visible sur la figure 4, le CPMM et la LMSR affichent un fort LVR aux prix extrêmes (proches de 0 ou 1). Bien que la volatilité soit faible près de ces points (cf. figure 3), la valeur du pool décroît plus vite à prix extrême. Un AMM uniforme devrait donc offrir moins de liquidité à ces prix — exactement ce que fait le pm-AMM (cf. figure 2).
Travaux antérieurs
Les AMM trouvent leurs racines dans les marchés prédictifs et les règles de notation comme la LMSR. Ces travaux ont mené à la découverte des CFMM (Constant Function Market Makers), comme Uniswap v2, caractérisés par une relation invariante entre les réserves. Ces mécanismes dominent aujourd’hui les DEX.
Récemment, une perspective issue de l’économie financière a été appliquée à l’étude des coûts des AMM, notamment via le LVR, principalement dans le cadre du GBM. Or, la dynamique des marchés prédictifs est très différente : gains bornés, durée limitée. Taleb a proposé des dynamiques basées sur des processus observables de vote, tandis que nous développons une approche fondée sur un processus gaussien observable.
Des recherches appliquées ont déjà exploré la conception d’AMM pour actifs non-GBM. Exemple : StableSwap, conçu pour les paires de stablecoins, repose sur l’idée intuitive de concentrer la liquidité autour d’un prix d’équilibre, mais sans modélisation explicite du processus de prix. Un autre exemple est YieldSpace, un AMM pour obligations zéro-coupon. Bien que basé sur un modèle de pricing simple, il ne modélise pas l’évolution du taux d’intérêt.
Des travaux académiques ont aussi cherché à concevoir des modèles de marchés en temps réel à partir de croyances sur le prix. Par exemple, le cadre de Goyal et al. vise à maximiser la liquidité active attendue, et non à uniformiser la perte. Cela peut mener à des conclusions opposées aux nôtres. Par exemple, ils concluent que la LMSR (qui concentre la liquidité autour de 1) est adaptée si les LP s’attendent à un prix stable autour de 1 ; notre cadre justifie au contraire cette concentration si les prix peuvent diverger fortement (comme pour les jetons-résultats).
Modèles d’AMM
Market-makers automatiques
Considérons un marché prédictif sur un événement unique, avec un AMM échangeant deux actifs antagonistes. L’actif risqué x paie 1 $ si l’événement se produit, 0 sinon ; l’actif y paie l’inverse. L’AMM maintient une invariante f(x,y)=L, où f(·,·) est la fonction invariante des réserves (x,y), et L une constante. Étant donné le prix P de x (en dollars), la valeur du pool est :
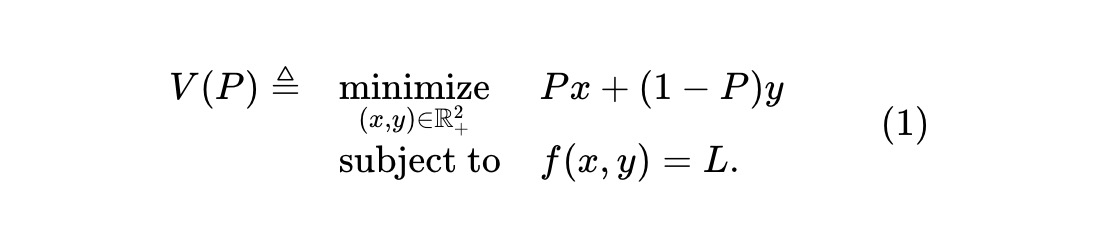
C’est la valeur du pool lorsque le prix de x est P. Comme détenir un unité de x et y équivaut à détenir 1 $, le prix de y doit être 1-P. Supposons des arbitragistes observant à chaque instant t le prix Pt de x (et donc 1-Pt pour y). Sans frais ni friction, ils surveillent l’AMM et profitent de toute erreur de prix. En maximisant leur profit, ils échangent contre l’AMM pour minimiser la valeur des réserves. Soit Vt la valeur des réserves au temps t (au prix Pt), alors Vt = V(Pt).
Exemple 1 : Pour un AMM à produit constant (CPMM), l’invariante est f(x,y)≜xy, et la valeur du pool est :
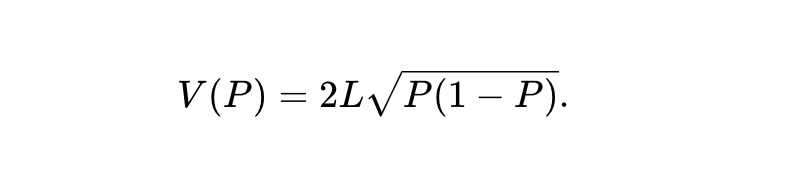
Exemple 2 : La règle de notation logarithmique (LMSR) de Robin Hanson peut être vue comme un AMM satisfaisant l’invariante suivante :
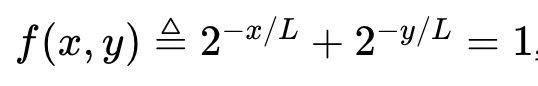
Sa fonction de valeur de pool est (proportionnelle à l’entropie binaire implicite du prix) :
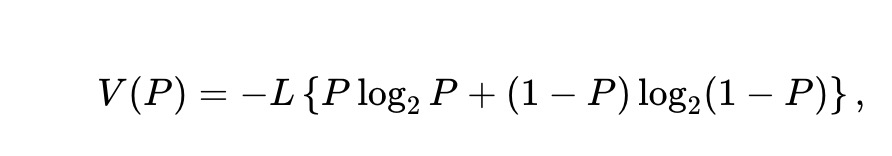
Soient x*(P) et y*(P) les solutions optimales du problème (1), supposées exister, uniques et suffisamment régulières en P. Alors, le résultat suivant, similaire au théorème 1 de Milionis et al., s’applique ici :
Théorème 1. Pour tout prix P ≥ 0, la fonction de valeur du pool satisfait :
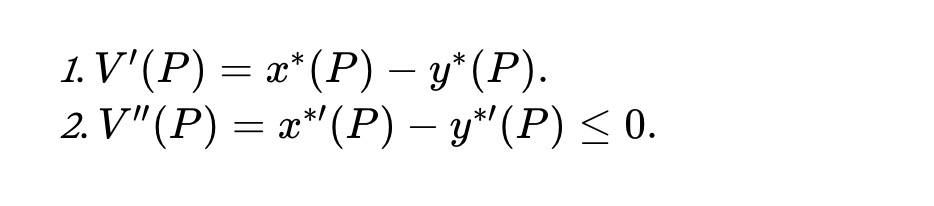
Dynamique gaussienne du score
Comment le prix de l’actif risqué évolue-t-il sous notre dynamique dite « gaussienne du score » ? Précisément, on suppose un processus aléatoire {Zt} sur t ∈ [0,T], où l’événement est déterminé par le signe de ZT : si ZT ≥ 0, x paie ; sinon, y paie. On interprète Zt comme l’écart de score entre deux équipes en compétition. Nous appelons Zt le « processus de score ». Notons que bien que le modèle suppose l’existence de ce processus, l’AMM n’a pas besoin de l’observer directement. Comme expliqué plus bas, l’AMM peut inférer la valeur courante du score à partir du prix marginal (après arbitrage) et du temps restant.
Nous supposons que Zt suit un mouvement brownien de volatilité σ > 0, soit dZt = σ dBt, avec Bt un mouvement brownien standard. Alors, le prix Pt de x au temps t est :
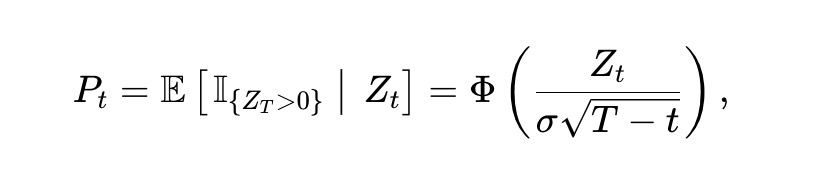
Où Φ(·) est la fonction de répartition normale standard (CDF). Par le lemme d’Itô, Pt suit :
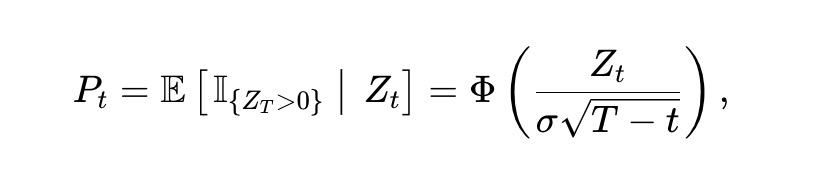
Où ϕ(·) est la densité normale standard, et Φ⁻¹(·) la CDF inverse. Bien que la dynamique du score et sa conversion en prix dépendent de σ, la dynamique isolée de Pt n’en dépend pas. La volatilité de cette dynamique en fonction du prix et du temps restant est illustrée figure 3.
AMM uniforme
D’après ce qui précède, si Vt désigne la valeur des réserves au temps t (au prix Pt), alors Vt = V(Pt). Par le lemme d’Itô, la valeur du pool évolue selon :
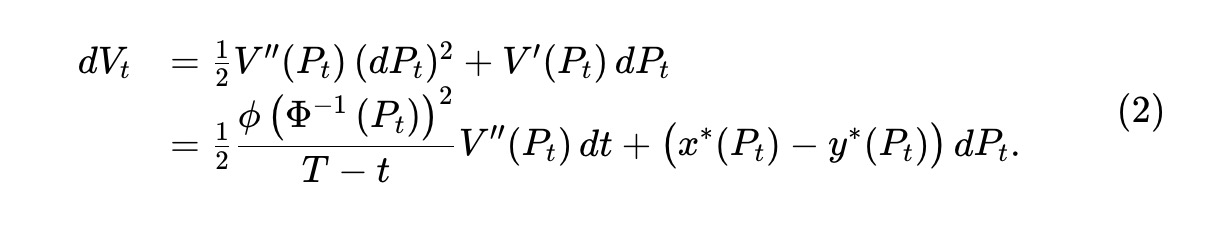
Comme Pt est une martingale, le second terme est une martingale (croissante ou décroissante). Mais d’après V(·) (voir théorème 1), le premier terme est une transformation négative, donc un processus décroissant. C’est le processus de « perte face au rééquilibrage » (LVR) de Milionis et al., capturant la valeur perdue face à des échanges défavorables avec des arbitragistes. Nous définissons le taux instantané de perte comme :
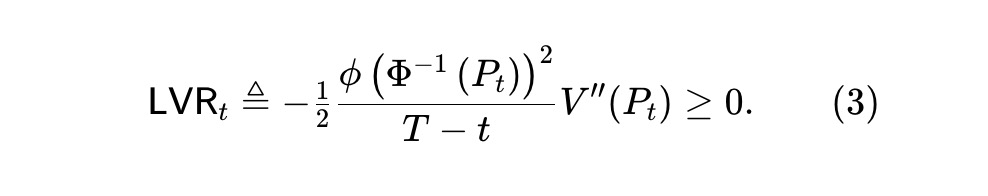
Milionis et al. montrent que pour un actif suivant un GBM, les seuls AMM uniformes sont ceux à moyenne géométrique. Pour un marché prédictif sous dynamique gaussienne du score, examiner (3) conduit à résoudre l’équation différentielle ordinaire (ODE) suivante pour un pool à LVR uniforme :
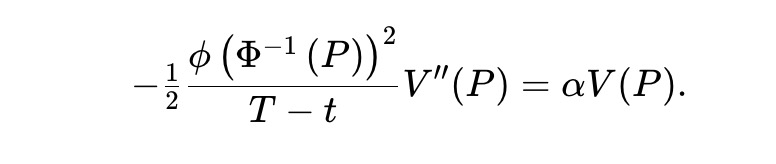
Ce n’est pas possible, car le membre gauche dépend de t, pas le droit. Le problème central est que la dynamique du GBM est invariante dans le temps, contrairement à la dynamique gaussienne du score.
Pour contourner cela, nous autorisons α à dépendre du temps : posons α = β/(T−t), avec β > 0, conduisant à :
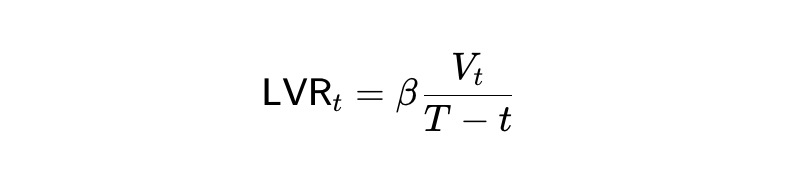
Ce qui équivaut à une ODE pour P ≥ 0. V(·) doit aussi satisfaire d’autres conditions, comme V''(P) ≤ 0 (voir théorème 1).
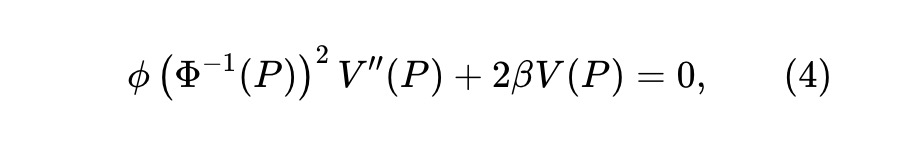
pm-AMM statique
Le changement de variable u = Φ⁻¹(P) simplifie cette ODE. Pour β = 1/2, une solution satisfaisant à la fois l’ODE et la condition de concavité existe :
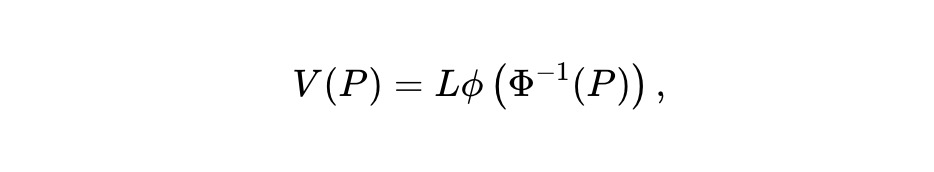
Les réserves en jetons x et y sont :
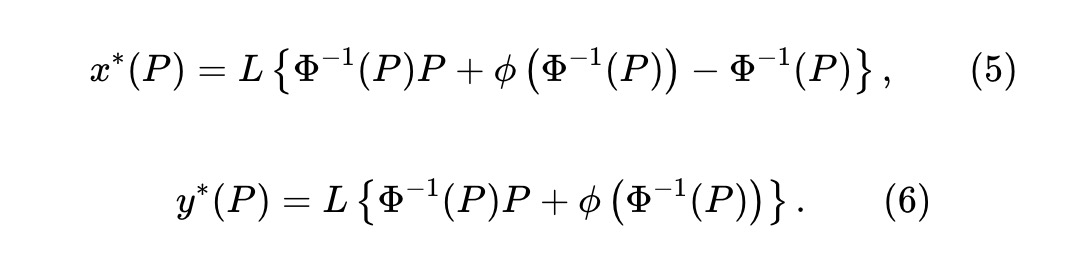
Ici, L ≥ 0 est un paramètre de liquidité, déterminant l’échelle du pool. En notant y*(P) − x*(P) = L Φ⁻¹(P), et en substituant dans (5), les réserves (x,y) doivent satisfaire l’invariante :
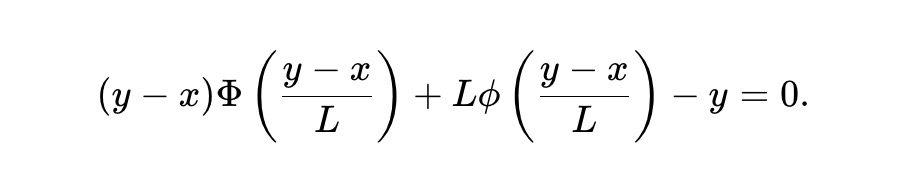
C’est la définition du pm-AMM statique. Par construction, cet AMM vérifie :
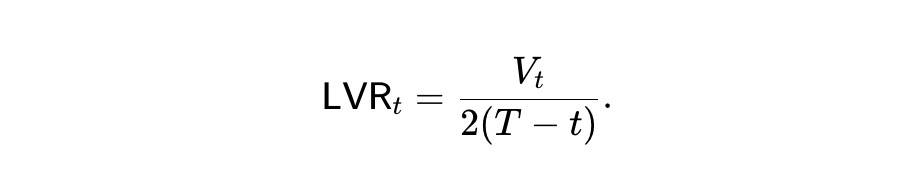
Soit V̄t = E[Vt] la valeur espérée du pool. À partir de (2) :
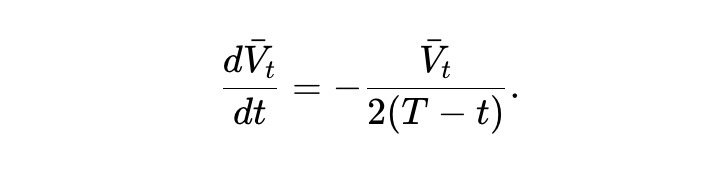
La solution de cette ODE donne :
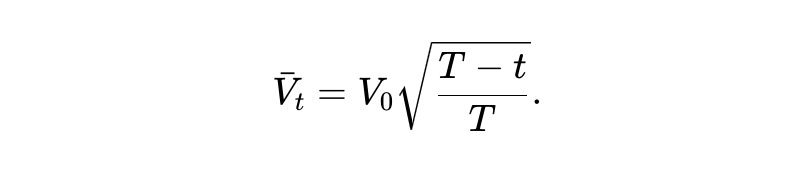
Autrement dit, en moyenne, la valeur du pool du pm-AMM statique décroît selon la racine carrée du temps restant.
pm-AMM dynamique
Un inconvénient du pm-AMM statique est que, bien que son LVR par dollar soit uniforme à tout prix, il varie dans le temps. Spécifiquement, la perte par dollar augmente à l’inverse du temps restant, tendant vers l’infini à l’échéance.
Liquidité dynamique. Nous imaginons une version dynamique du pm-AMM statique, où les LP retirent progressivement de la liquidité pour limiter les pertes. Supposons que la valeur du pool suive :
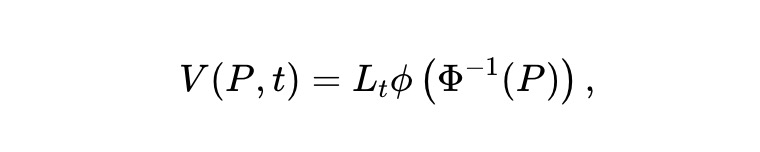
Où Lt est une fonction déterministe et régulière, indiquant comment la liquidité est retirée (ou ajoutée) au fil du temps. Appliquant Itô au processus Vt ≜ V(Pt,t) :
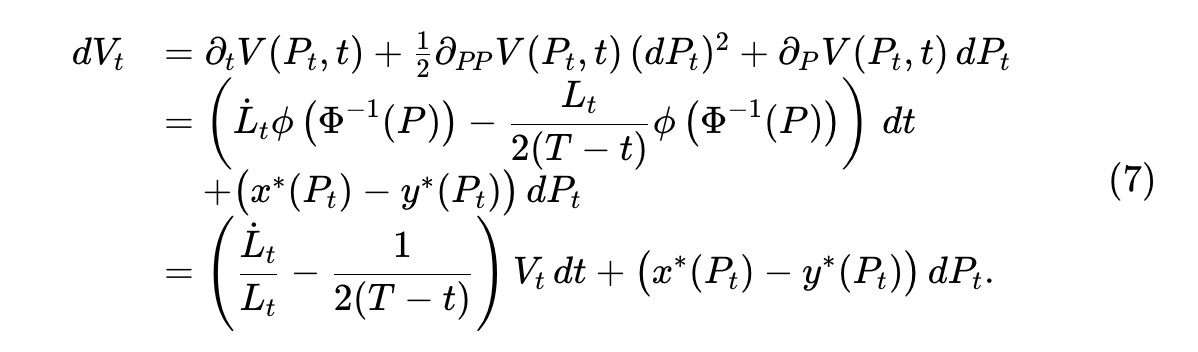
Soit Ct la valeur cumulée retirée. Comme la valeur du pool est linéaire en Lt, la valeur en dollars du changement de Lt est proportionnelle à Vt/Lt. On obtient :
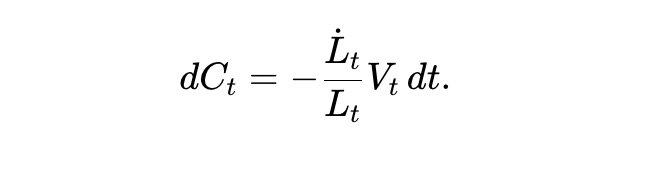
La richesse totale Wt des LP est la somme de la valeur du pool et de la liquidité retirée : Wt = Vt + Ct, et satisfait :
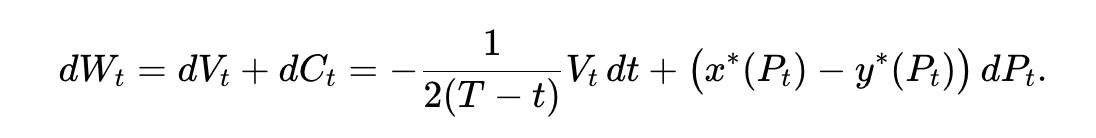
Ainsi, la richesse espérée W̄t ≜ E[Wt] vérifie, avec V̄t ≜ E[Vt] :
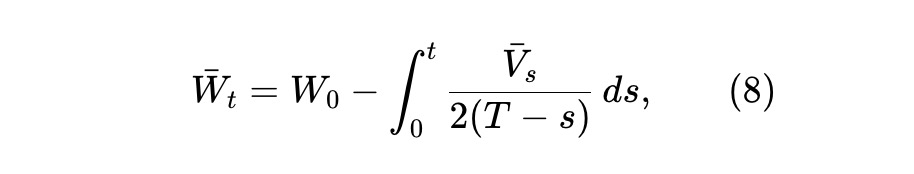
Choisissons maintenant une courbe de liquidité spécifique :
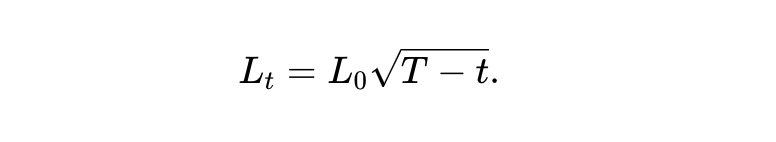
Nous appelons ceci le pm-AMM dynamique. D’après (7), la valeur espérée du pool V̄t = E[Vt] satisfait :
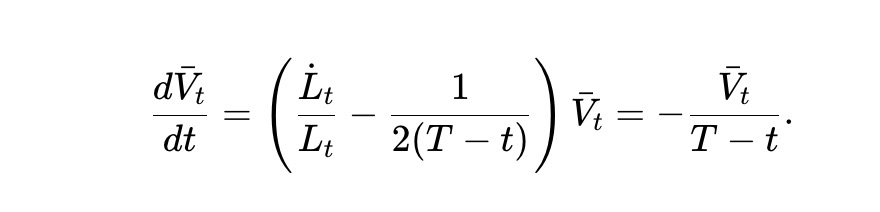
La solution est :
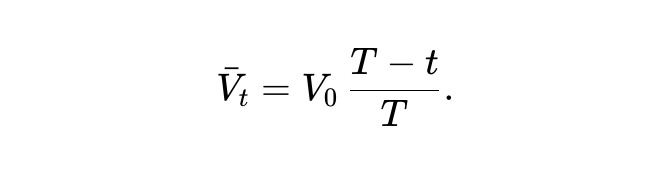
Autrement dit, dans le pm-AMM dynamique, la valeur espérée du pool décroît linéairement après retraits. De plus, héritant de la fonction de valeur du pm-AMM statique, le taux de perte LVR instantané est :
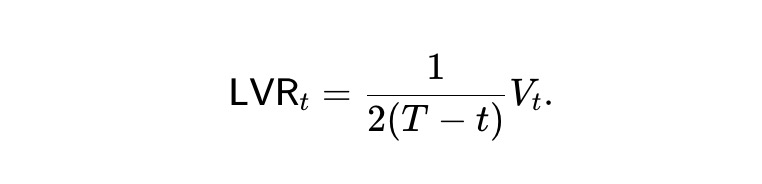
Le taux de perte espéré reste constant durant toute la période t. Ainsi, le pm-AMM dynamique perd de l’argent face aux arbitragistes à un rythme constant (en moyenne).
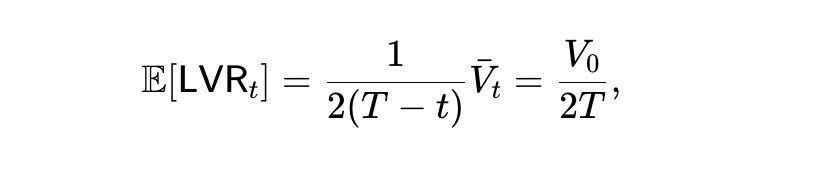
Enfin, d’après (8), le processus de richesse espéré est illustré ci-dessous. La moitié de la richesse initiale est perdue à l’échéance.
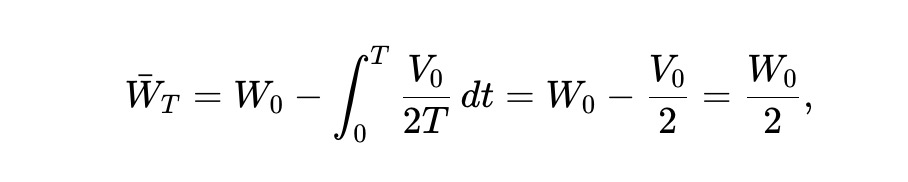
Conclusion
Le pm-AMM pourrait convenir aux marchés prédictifs guidés par des dynamiques similaires à notre modèle gaussien du score. Plus largement, notre recherche suggère que les AMM uniformes pourraient être adaptés à d'autres types d'actifs, comme les obligations, options et autres dérivés.
Bienvenue dans la communauté officielle TechFlow
Groupe Telegram :https://t.me/TechFlowDaily
Compte Twitter officiel :https://x.com/TechFlowPost
Compte Twitter anglais :https://x.com/BlockFlow_News
















