
Cơ sở lý thuyết về việc xây dựng danh mục đầu tư tài sản mã hóa mạnh mẽ bằng chiến lược đa yếu tố
Tuyển chọn TechFlowTuyển chọn TechFlow

Cơ sở lý thuyết về việc xây dựng danh mục đầu tư tài sản mã hóa mạnh mẽ bằng chiến lược đa yếu tố
"Yếu tố" chính là "chỉ báo" trong phân tích kỹ thuật, hay còn gọi là "đặc trưng" trong học máy trí tuệ nhân tạo, là nguyên nhân quyết định sự tăng giảm lợi suất của tiền mã hóa.
Lời nói đầu
Vào tháng 6 năm ngoái, tôi đã phác thảo một ý tưởng đơn giản về việc sử dụng mô hình đa yếu tố để lựa chọn tiền mã hóa.
Một năm sau, chúng tôi đã bắt tay vào nghiên cứu và phát triển chiến lược đa yếu tố dành riêng cho thị trường tài sản mã hóa, đồng thời xây dựng toàn bộ khung chiến lược thành một loạt bài viết có tên “Xây dựng danh mục đầu tư tài sản mã hóa mạnh mẽ bằng chiến lược đa yếu tố”.
Khung tổng thể của loạt bài này như sau (có thể điều chỉnh nhỏ nếu cần):
1. Cơ sở lý thuyết mô hình đa yếu tố
2. Xây dựng yếu tố đơn lẻ
-
Tiền xử lý dữ liệu yếu tố
-
Lọc dữ liệu
-
Xử lý giá trị bất thường: giá trị cực đoan, sai sót, giá trị trống
-
Chuẩn hóa
-
Trung tính hóa: ngành nghề, thị trường, vốn hóa
-
-
Đánh giá hiệu quả yếu tố
- Tỷ lệ thông tin IC, lợi nhuận, tỷ suất Sharpe, tỷ lệ quay vòng
3. Tổng hợp nhóm yếu tố lớn
-
Phân tích cộng tuyến giữa các yếu tố
-
Loại bỏ cộng tuyến bằng phương pháp trực giao
-
Phương pháp trọng số cổ điển → tổng hợp yếu tố
-
Trọng số bằng nhau, trọng số theo IC trượt, trọng số theo IC_IR
-
Kiểm định yếu tố tổng hợp: lợi nhuận, lợi nhuận theo nhóm, lợi nhuận theo trọng số giá trị yếu tố, IC yếu tố tổng hợp, tỷ lệ quay vòng theo nhóm
-
-
Các phương pháp trọng số khác (khi mối quan hệ giữa yếu tố và lợi nhuận là phi tuyến): học máy, học tăng cường (không xem xét do đặc thù ngành tiền mã hóa)
4. Tối ưu hóa danh mục rủi ro
Sau đây là nội dung chính của bài đầu tiên – “Phần cơ sở lý thuyết”.
1. “Yếu tố” là gì
“Yếu tố” chính là “chỉ báo” trong phân tích kỹ thuật, hay “đặc trưng” trong học máy trí tuệ nhân tạo – là nguyên nhân quyết định sự tăng giảm lợi suất của tiền mã hóa.
Nhóm chúng tôi chia các loại yếu tố phổ biến trong lĩnh vực tiền mã hóa thành: yếu tố cơ bản, yếu tố chuỗi, yếu tố khối lượng-giá, yếu tố phái sinh, yếu tố thay thế và yếu tố vĩ mô.
Mục đích cuối cùng của việc khai thác và tính toán “yếu tố” là để xác định chính xác lợi suất kỳ vọng của tài sản.
2. Cách tính “yếu tố”
(1) Suy luận mô hình đa yếu tố
Xuất phát: Mô hình đơn yếu tố – CAPM
Nghiên cứu về yếu tố bắt nguồn từ những năm 1960, khi mô hình định giá tài sản vốn (Capital Asset Pricing Model - CAPM) ra đời, mô hình này định lượng cách rủi ro ảnh hưởng đến chi phí vốn của doanh nghiệp, từ đó tác động đến lợi suất kỳ vọng. Theo lý thuyết CAPM, lợi suất kỳ vọng vượt trội của một tài sản riêng lẻ được xác định bởi mô hình hồi quy tuyến tính đơn biến như sau:
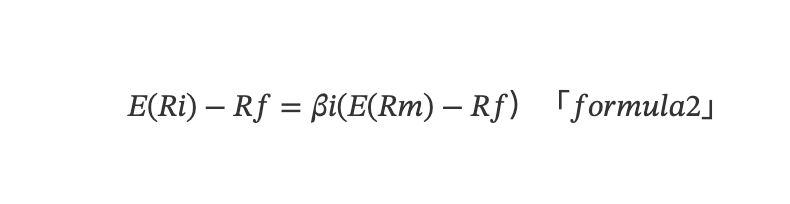
E(Ri) là kỳ vọng toán học, Ri là lợi suất của tài sản, Rf là lợi suất phi rủi ro, Rm là lợi suất của danh mục thị trường, βi = Cov(Ri,Rm)/Var(Rm) phản ánh mức độ nhạy cảm của lợi suất tài sản đối với lợi suất thị trường, còn gọi là mức độ phơi nhiễm rủi ro thị trường của tài sản.
Giải thích bổ sung:
-
Trong thị trường tài chính, “rủi ro” và “lợi nhuận” về bản chất là hai mặt của cùng một vấn đề.
-
Hiểu sâu hơn về βi dưới góc nhìn thống kê
CAPM có thể coi là mô hình hồi quy hai biến không có hệ số chặn Yi = β1 + β2 · X (β1 = 0), dùng phương pháp bình phương tối thiểu thông thường (OLS) để ước lượng các tham số mô hình, trong đó β1 = β2 = Σ(X-μX)(Y-μY)/ Σ(X-μX)² = Cov(X,Y)/Var(X).
β1 đo lường mức độ thay đổi trung bình của biến phụ thuộc (lợi suất tài sản i) khi biến độc lập (lợi suất thị trường) thay đổi một đơn vị. Trong lĩnh vực tài chính, mức độ thay đổi này được hiểu là độ “nhạy cảm” hoặc “phơi nhiễm” của Y đối với X.
β>1 khuếch đại biến động thị trường
β = 1 biến động hoàn toàn giống thị trường
0<β<1 biến động cùng chiều nhưng nhỏ hơn thị trường
β≤ 0 biến động ngược chiều thị trường
1. Hiểu sâu hơn về βi dưới góc nhìn rủi ro và lợi nhuận trong tài chính
Danh mục đầu tư có hai loại rủi ro: rủi ro hệ thống (rủi ro thị trường, rủi ro không thể triệt tiêu) và rủi ro phi hệ thống (rủi ro có thể triệt tiêu). βi là rủi ro hệ thống, dù cấu trúc danh mục như thế nào thì rủi ro này vẫn tồn tại và không thể loại bỏ. Còn αi nhắc đến bên dưới là rủi ro phi hệ thống, có thể được bù trừ bằng các chiến lược khác nhau.
Mô hình CAPM là mô hình yếu tố tuyến tính đơn giản nhất, chỉ ra rằng lợi suất vượt trội của tài sản chỉ phụ thuộc vào lợi suất vượt trội kỳ vọng của danh mục thị trường (yếu tố thị trường) và mức độ phơi nhiễm rủi ro thị trường của tài sản. Mô hình này đặt nền móng lý thuyết cho hàng loạt nghiên cứu về mô hình định giá đa yếu tố tuyến tính sau này.
Phát triển: Mô hình đa yếu tố – APT
Dựa trên CAPM, người ta nhận thấy lợi suất của các tài sản khác nhau bị ảnh hưởng bởi nhiều yếu tố, từ đó Lý thuyết Định giá Chênh lệch (Arbitrage Pricing Theory - APT) ra đời, xây dựng mô hình đa yếu tố tuyến tính:
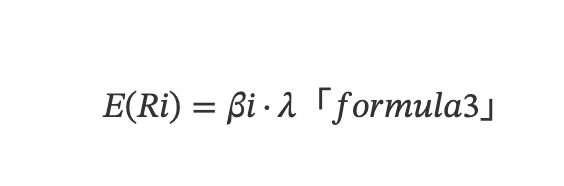
Trong đó, E(Ri) biểu thị lợi suất kỳ vọng của tài sản i, λ biểu thị lợi suất kỳ vọng của yếu tố (hay còn gọi là phí yếu tố). Công thức (2) sử dụng E(Ri) thay cho E(Ri) - Rf trong mô hình CAPM để biểu thị lợi suất kỳ vọng. Khi dùng danh mục trung tính về vốn được xây dựng bằng chiến lược mua bán chênh lệch (long-short), Rf bị triệt tiêu, lợi suất kỳ vọng của toàn bộ danh mục chính là chênh lệch giữa lợi suất kỳ vọng của phần long và short, do đó dùng E(Ri) mang tính tổng quát hơn.
Trưởng thành: Mô hình đa yếu tố – Lợi nhuận Alpha & Beta
Kết hợp thực tế sai số định giá tồn tại trên thị trường tài chính và mô hình APT, xét theo góc độ thời gian, lợi suất kỳ vọng của một tài sản đơn lẻ được xác định bởi mô hình hồi quy tuyến tính đa biến như sau:
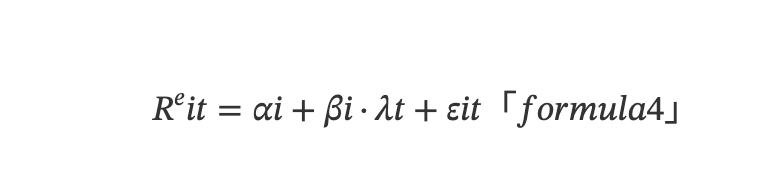
Trong đó, Rᵉit là lợi suất của tài sản i tại thời điểm t, λt là lợi suất yếu tố tại thời điểm t (phí yếu tố), εit là nhiễu ngẫu nhiên tại thời điểm t. αi là sai số định giá giữa lợi suất kỳ vọng thực tế và lợi suất kỳ vọng ngầm định trong mô hình đa yếu tố. Nếu αi có ý nghĩa thống kê khác 0, nó đại diện cho cơ hội kiếm lợi nhuận vượt trội. βi = Cov(Ri,λ)/Var(λ) là mức độ phơi nhiễm yếu tố hay tải yếu tố của tài sản i, phản ánh mức độ nhạy cảm của lợi suất tài sản đối với lợi suất yếu tố.
Mô hình đa yếu tố tập trung vào sự khác biệt về lợi suất kỳ vọng giữa các tài sản ở một thời điểm (góc nhìn mặt cắt), về bản chất là mô hình về trung bình, trong khi lợi suất kỳ vọng là giá trị trung bình của lợi suất trên chuỗi thời gian. Dựa trên (3), ta suy ra mô hình hồi quy tuyến tính đa biến theo góc nhìn mặt cắt:
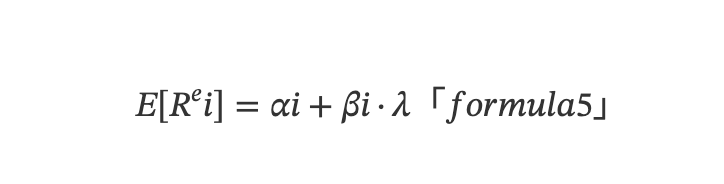
Trong đó, E[Rᵉi] là lợi suất vượt trội kỳ vọng của tài sản i, εit lấy trung bình theo thời gian nên E(εit)=0.
Giải thích bổ sung:
Từ góc nhìn học thuật, theo lý thuyết hiệu quả thị trường, một danh mục hiệu quả nên có rủi ro có thể triệt tiêu hoàn toàn bằng 0, lợi suất thực tế bằng lợi suất kỳ vọng, và lợi suất kỳ vọng chỉ phụ thuộc vào rủi ro hệ thống của thị trường, tức là E[Rᵉi] = βi · λ, không tồn tại lợi suất vượt trội (Abnormal Return - AR), hay AR = Ri - E(Rᵉi) = 0. Nhưng trên thực tế, thị trường tài chính thường không hiệu quả, tồn tại lợi suất vượt trội, tức là AR = α.
Giả sử danh mục gồm N tài sản, và mở rộng lợi suất yếu tố λ tương ứng cho mỗi tài sản i theo từng yếu tố khác nhau, ta có được lợi suất danh mục theo mô hình đa yếu tố như sau:
Rp = ∑ᴺᵢ₌₁Wi(αi+∑ᴹⱼ₌₁βᵢⱼfᵢⱼ)
Trong đó, Rp là lợi suất vượt trội của danh mục, Wi là trọng số của mỗi tài sản trong danh mục, βij là mức độ phơi nhiễm rủi ro của mỗi tài sản trên từng yếu tố, λ = ∑ᴹⱼ₌₁βᵢⱼfᵢⱼ, fᵢⱼ là lợi suất yếu tố ứng với mỗi đơn vị tải yếu tố của từng yếu tố cho mỗi tài sản.
Kết hợp kiến thức thống kê, mô hình này ngầm chứa ba giả định:
-
Lợi suất Beta và Alpha của mỗi tài sản không tương quan: Cov(αi,βiλ)=0
-
Lợi suất đặc thù giữa các tài sản khác nhau cũng không tương quan: Cov(αi,αj)=0
-
Yếu tố phải có liên hệ với lợi suất tài sản: Cov(Rᵉi,βiλ)≠0
Giải thích tổng hợp về lợi nhuận Beta và Alpha:
Áp dụng vào thị trường tài chính cụ thể, βiλ là lợi nhuận Beta thuộc về hiệu suất chung của thị trường, αi là lợi nhuận Alpha do đặc điểm riêng của tài sản mang lại – tức là vượt trội so với thị trường bao nhiêu điểm. Lợi suất của mỗi tài sản đều gồm hai phần Beta và Alpha. Người ta có thể dùng giá trị αi tương ứng của mỗi tài sản trong mô hình đa yếu tố để xếp hạng hoặc gán trọng số cho tài sản, từ đó xây dựng danh mục, đồng thời dùng hợp đồng tương lai để bán khống phần lợi nhuận Beta nhằm phòng ngừa rủi ro, từ đó thu được lợi nhuận Alpha.
(2) Độ biến động của mô hình đa yếu tố
Khi xây dựng danh mục đầu tư, cần cân bằng giữa rủi ro và lợi nhuận, do đó cần chuyển mô hình trên thành bài toán quy hoạch có ràng buộc để giải. Rủi ro danh mục chính là độ biến động σ²p của danh mục, phần sau đây sẽ suy luận σ²p. Phân tích chi tiết về xây dựng danh mục sẽ trình bày ở phần “Tối ưu hóa danh mục rủi ro”.
Dựa trên biểu diễn ma trận của công thức (3): Rp = W(β ∧ + α), ta có độ biến động danh mục:
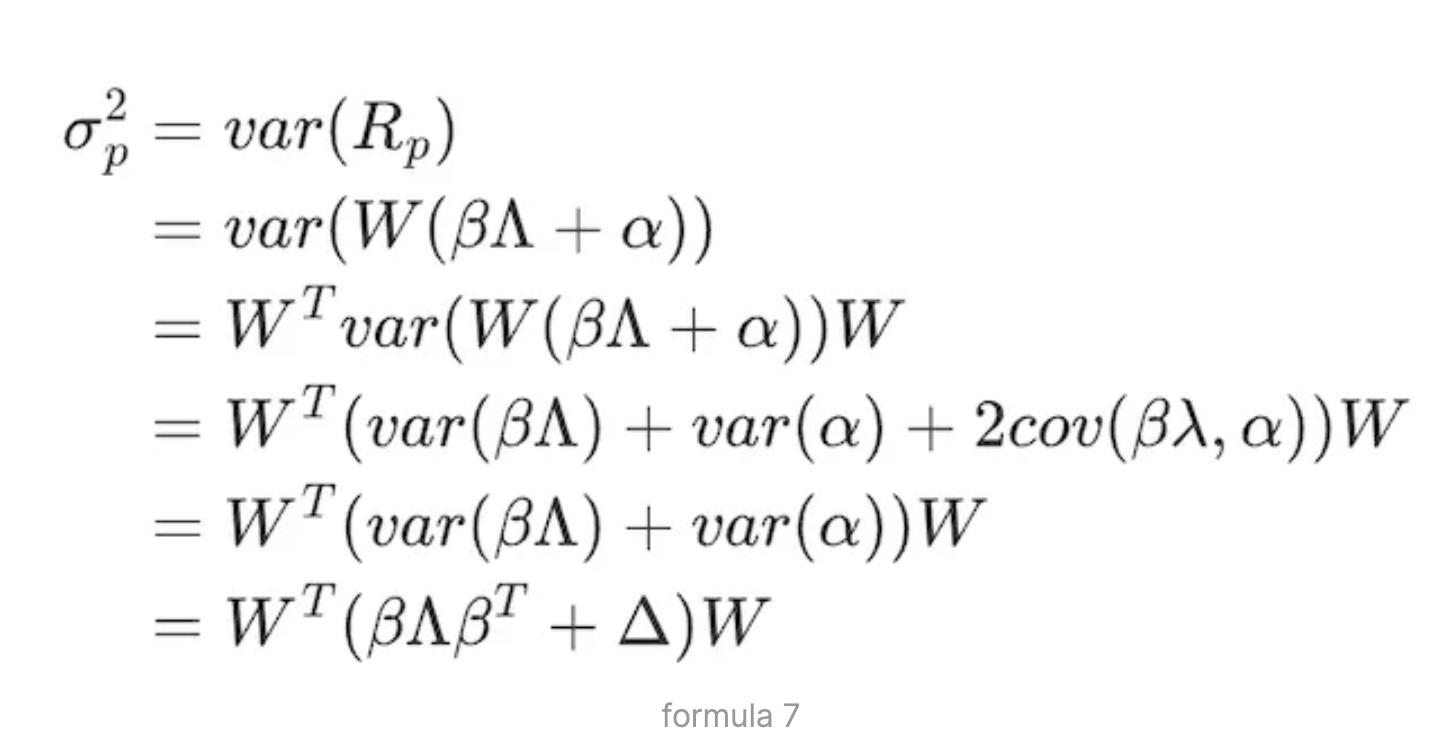
Trong đó, W là ma trận trọng số tài sản, β là ma trận trọng số yếu tố, biểu thị ma trận tải yếu tố N×K của N tài sản trên K yếu tố rủi ro:

∧ biểu thị ma trận hiệp phương sai lợi suất yếu tố K×K của K yếu tố:

Theo giả định 3, lợi suất đặc thù giữa các tài sản không tương quan, suy ra ma trận Δ có dạng:

Chào mừng tham gia cộng đồng chính thức TechFlow
Nhóm Telegram:https://t.me/TechFlowDaily
Tài khoản Twitter chính thức:https://x.com/TechFlowPost
Tài khoản Twitter tiếng Anh:https://x.com/BlockFlow_News















