
Théorie fondamentale de la construction d'un portefeuille d'actifs cryptographiques robuste à l'aide de stratégies multifactorielles
TechFlow SélectionTechFlow Sélection

Théorie fondamentale de la construction d'un portefeuille d'actifs cryptographiques robuste à l'aide de stratégies multifactorielles
Un « facteur » correspond à un « indicateur » en analyse technique ou à une « caractéristique » en apprentissage automatique de l'intelligence artificielle, et constitue la raison déterminante des variations de rendement des cryptomonnaies.
Préface
En juin dernier, j'avais esquissé une idée simple consistant à utiliser un modèle multifactoriel pour sélectionner des cryptomonnaies.
Un an plus tard, nous avons entamé le développement d'une stratégie multifactorielle adaptée au marché des actifs cryptographiques, et rédigé l'ensemble du cadre stratégique sous forme d'une série d'articles intitulée « Construire un portefeuille d'actifs cryptographiques robuste grâce à une stratégie multifactorielle ».
Voici la structure générale de cette série (sujette à ajustements mineurs) :
I. Fondements théoriques du modèle multifactoriel
II. Construction des facteurs individuels
-
Prétraitement des données factorielles
-
Filtrage des données
-
Traitement des valeurs aberrantes : extrêmes, erreurs, données manquantes
-
Standardisation
-
Neutralisation : secteur, marché, capitalisation boursière
-
-
Évaluation de l'efficacité des facteurs
- Ratio d'information IC, rendement, ratio de Sharpe, taux de rotation
III. Agrégation des grands types de facteurs
-
Analyse de la colinéarité entre facteurs
-
Élimination de la colinéarité par orthogonalisation
-
Méthodes classiques de pondération → facteur agrégé
-
Pondération égale, pondération par IC glissant, pondération par IC_IR
-
Tests du facteur agrégé : rendement, rendement par groupe, rendement pondéré par valeur du facteur, IC du facteur agrégé, taux de rotation par groupe
-
-
Autres méthodes de pondération (relation non linéaire entre facteur et rendement) : apprentissage automatique, apprentissage par renforcement (non pris en compte en raison des particularités du secteur des cryptomonnaies)
IV. Optimisation du portefeuille de risque
Voici le contenu principal du premier article, « Fondements théoriques ».
I. Qu'est-ce qu’un « facteur » ?
Un « facteur » correspond à un « indicateur » en analyse technique ou à une « caractéristique » en apprentissage automatique. C’est ce qui explique les variations du rendement des cryptomonnaies.
Notre équipe classe les facteurs courants dans le domaine des cryptomonnaies en six catégories : facteurs fondamentaux, facteurs sur chaîne (on-chain), facteurs prix-volume, facteurs dérivés, facteurs alternatifs et facteurs macroéconomiques.
L’objectif ultime de l’extraction et du calcul des « facteurs » est de pouvoir estimer précisément le rendement attendu d’un actif.
II. Calcul des « facteurs »
(1) Dérivation du modèle multifactoriel
Origine : modèle monofactoriel — CAPM
Les recherches sur les facteurs remontent aux années 1960, avec l’apparition du modèle d’évaluation des actifs financiers (Capital Asset Pricing Model, CAPM). Ce modèle quantifie comment le risque influence le coût du capital d’une entreprise, et donc son rendement attendu. Selon la théorie du CAPM, le rendement excédentaire attendu d’un actif unique peut être déterminé par le modèle linéaire suivant :
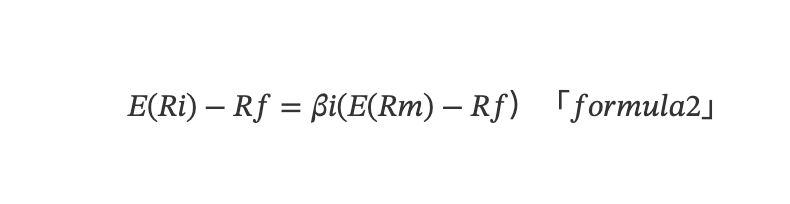
E(Ri) désigne l’espérance mathématique, Ri le rendement de l’actif, Rf le taux sans risque, Rm le rendement du portefeuille de marché, et βi = Cov(Ri,Rm)/Var(Rm) mesure la sensibilité du rendement de l’actif au rendement du marché, aussi appelée exposition de l’actif au risque de marché.
Compléments d'explication :
-
Dans les marchés financiers, « risque » et « rendement » sont essentiellement deux faces d’une même réalité.
-
Du point de vue statistique, compréhension approfondie de βi
Le CAPM peut être vu comme un modèle de régression bivarié sans terme constant Yi = β1 + β2 · X (β1 = 0). Les paramètres du modèle sont estimés par la méthode des moindres carrés ordinaires (OLS), où β1 = β2 = Σ(X-μX)(Y-μY)/ Σ(X-μX)² = Cov(X,Y)/Var(X).
β1 mesure le changement moyen du rendement de l’actif i (variable expliquée) lorsque le rendement du marché (variable explicative) varie d’une unité. En finance, ce degré de variation est interprété comme la « sensibilité » ou le niveau d’« exposition » de Y à X.
β > 1 amplifie les fluctuations du marché
β = 1 reflète exactement les fluctuations du marché
0 < β < 1 : variation dans le même sens que le marché, mais d’amplitude moindre
β ≤ 0 : variation inverse à celle du marché
1. Du point de vue financier du risque et du rendement, compréhension approfondie de βi
Un portefeuille comporte deux types de risques : le risque systématique (ou risque de marché, risque non diversifiable) et le risque non systématique (risque diversifiable). βi représente le risque systématique, inhérent au système, impossible à éliminer quelle que soit la composition du portefeuille. Le terme αi mentionné ci-dessous correspond au risque non systématique, qui peut être neutralisé via des stratégies spécifiques.
Le modèle CAPM est le modèle factoriel linéaire le plus simple. Il affirme que le rendement excédentaire d’un actif dépend uniquement du rendement excédentaire attendu du marché (facteur marché) et de sa sensibilité au risque de marché. Ce modèle a posé les bases théoriques pour de nombreux modèles multifactoriels linéaires développés par la suite.
Développement : modèle multifactoriel — APT
À partir du CAPM, on s’est rendu compte que les rendements des différents actifs étaient influencés par plusieurs facteurs. La Théorie de l’Évaluation par Arbitrage (Arbitrage Pricing Theory, APT) a alors été introduite, permettant de construire un modèle linéaire multifactoriel :
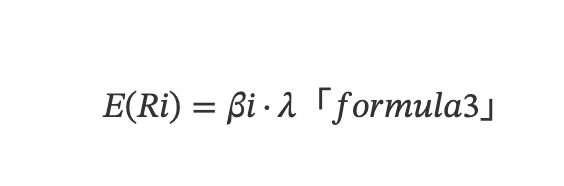
Ici, E(Ri) désigne le rendement attendu de l’actif i, et λ représente le rendement attendu du facteur (prime de facteur). Dans la formule (2), E(Ri) remplace E(Ri) - Rf du modèle CAPM pour exprimer le rendement attendu. En utilisant des portefeuilles neutres en capital construits par couverture long/court, le taux sans risque Rf s’annule, et le rendement attendu global devient la différence entre les rendements attendus des positions longues et courtes. L’utilisation de E(Ri) est donc plus générale.
Maturation : modèle multifactoriel — rendement Alpha et rendement Beta
En tenant compte des erreurs de valorisation présentes sur les marchés financiers réels ainsi que du modèle APT, le rendement attendu d’un actif individuel peut être décrit, du point de vue temporel, par le modèle linéaire multiple suivant :
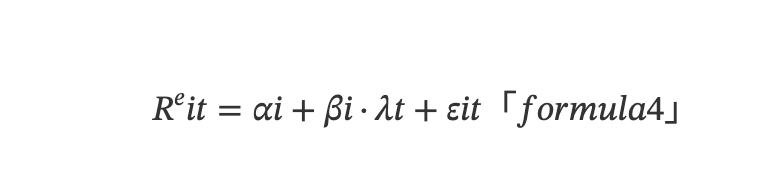
Où Rᵉit désigne le rendement de l’actif i au moment t, λt le rendement du facteur au moment t (prime de facteur), et εit la perturbation aléatoire au moment t. αi représente l’écart entre le rendement attendu réel de l’actif i et celui implicite dans le modèle multifactoriel. Si cet écart est statistiquement significatif par rapport à zéro, il indique une opportunité de rendement excédentaire. βi = Cov(Ri,λ)/Var(λ) mesure l’exposition au facteur (ou charge factorielle) de l’actif i, reflétant la sensibilité de son rendement aux variations du facteur.
Le modèle multifactoriel se concentre sur les différences transversales du rendement attendu des actifs. Il s’agit fondamentalement d’un modèle de moyenne, puisque le rendement attendu est la moyenne du rendement sur une série chronologique. À partir de (3), on peut dériver le modèle linéaire multiple en coupe instantanée :
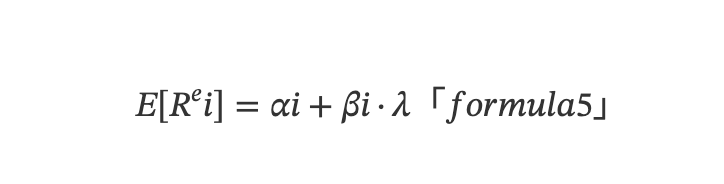
Où E[Rᵉi] est le rendement excédentaire attendu de l’actif i, et E(εit)=0 car εit est moyenné dans le temps.
Complément d'explication :
Du point de vue académique, selon la théorie de l’efficience des marchés, un portefeuille efficace doit avoir un risque diversifiable nul. Dans ce cas, le rendement réel égale le rendement attendu, et ce dernier dépend uniquement du risque systématique du marché : E[Rᵉi] = βi · λ. Il n’y a alors pas de rendement excédentaire (Abnormal Return, AR), soit AR = Ri - E(Rᵉi) = 0. Mais dans la réalité financière, les marchés sont souvent inefficaces, ce qui laisse place à des rendements excédentaires, autrement dit AR = α.
Supposons qu’un portefeuille soit composé de N actifs, et que le rendement factoriel λ de chaque actif i soit décomposé selon différents facteurs. On obtient alors le rendement du portefeuille multifactoriel suivant :
Rp = ∑ᴺᵢ₌₁Wi(αi+∑ᴹⱼ₌₁βᵢⱼfᵢⱼ)
Où Rp est le rendement excédentaire du portefeuille, Wi la part de chaque actif dans le portefeuille, βij l’exposition au risque du facteur j pour l’actif i, λ = ∑ᴹⱼ₌₁βᵢⱼfᵢⱼ, et fᵢⱼ le rendement du facteur j par unité de charge factorielle pour l’actif i.
En lien avec les concepts statistiques, ce modèle repose sur trois hypothèses implicites :
-
Les rendements Beta et Alpha de chaque actif sont non corrélés : Cov(αi,βiλ)=0
-
Les rendements spécifiques (idiosyncratiques) de différents actifs ne sont pas corrélés : Cov(αi,αj)=0
-
Les facteurs doivent être corrélés au rendement de l’actif : Cov(Rᵉi,βiλ)≠0
Explication combinée des rendements Beta et Alpha :
Appliqué aux marchés financiers concrets, βiλ représente le rendement Beta lié à la performance globale du marché, tandis que αi est le rendement Alpha généré par les caractéristiques propres à l’actif, c’est-à-dire de combien il surperforme le marché. Le rendement total de chaque actif résulte de la somme du rendement Beta et du rendement Alpha. Grâce au modèle multifactoriel, on peut attribuer une note ou un poids à chaque actif selon sa valeur αi, construire un portefeuille, puis vendre à découvert les futures pour couvrir la partie Beta, afin de capturer uniquement le rendement Alpha.
(2) Volatilité du modèle multifactoriel
Lors de la construction d’un portefeuille, il faut trouver un équilibre entre risque et rendement, ce qui revient à résoudre un problème d’optimisation sous contraintes. Le risque du portefeuille correspond à sa volatilité σ²p. Nous allons maintenant dériver σ²p. Une analyse détaillée de la construction du portefeuille sera présentée dans la section « Optimisation du portefeuille de risque ».
À partir de l’expression matricielle de la formule (3), Rp = W(β ∧ + α), on obtient la volatilité du portefeuille :
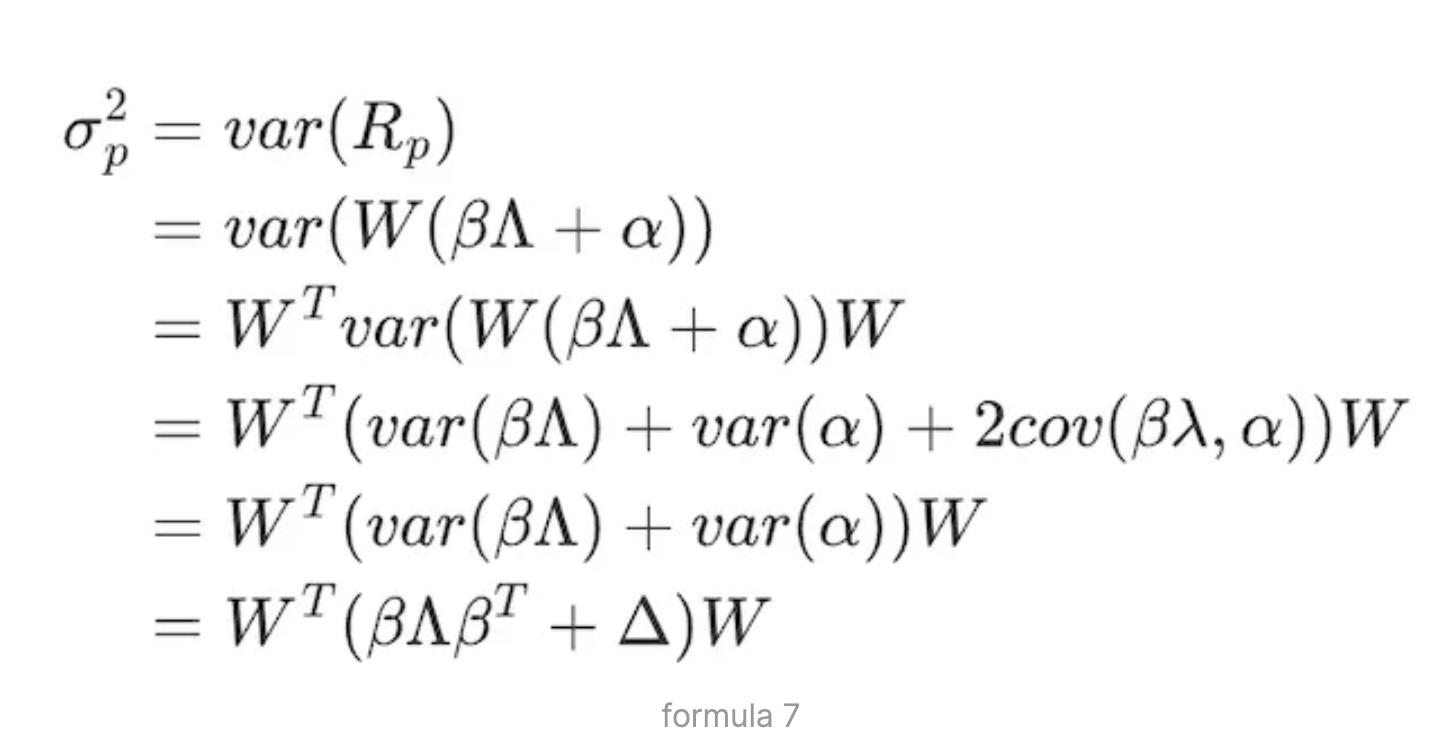
Où W est la matrice des poids des actifs, β la matrice des facteurs, représentant la matrice N×K des charges factorielles des N actifs sur K facteurs de risque :

∧ représente la matrice de covariance des rendements des K facteurs, de dimension K×K :

D’après l’hypothèse 3, les rendements spécifiques des différents actifs ne sont pas corrélés. On obtient donc la matrice Δ suivante :

Bienvenue dans la communauté officielle TechFlow
Groupe Telegram :https://t.me/TechFlowDaily
Compte Twitter officiel :https://x.com/TechFlowPost
Compte Twitter anglais :https://x.com/BlockFlow_News















