
Nouvel article de Vitalik : Principes mathématiques pour une division raisonnable des phases L2
TechFlow SélectionTechFlow Sélection

Nouvel article de Vitalik : Principes mathématiques pour une division raisonnable des phases L2
Une combinaison de gouvernance humaine et de mécanismes rend la deuxième phase des L2 plus antifragile.
Rédaction : Vitalik Buterin
Traduction : Wenser, Odaily Star Daily
Note de l'éditeur : Le débat sur les trois phases de sécurité des rollups Ethereum a toujours été un sujet central au sein de la communauté écosystémique d'Ethereum. Cela ne concerne pas seulement la stabilité du fonctionnement du réseau principal Ethereum et des réseaux L2, mais aussi l'état réel du développement des réseaux L2. Récemment, un membre de la communauté Ethereum, Daniel Wang, a proposé sur la plateforme X l'étiquette #BattleTested pour désigner la phase 2 des réseaux L2, suggérant que seuls les réseaux L2 dont le code et la configuration sont déployés sur le réseau principal Ethereum depuis plus de 6 mois, avec une valeur totale verrouillée (TVL) continue supérieure à 100 millions de dollars, dont au moins 50 millions en ETH et en principales stablecoins, peuvent prétendre à cette reconnaissance. Cette reconnaissance serait évaluée dynamiquement afin d'éviter l'apparition de « fantômes blockchain ». Par la suite, Vitalik Buterin, cofondateur d’Ethereum, a fourni une analyse détaillée et partagé son point de vue sur ce sujet, que nous traduisons ci-dessous.
Les trois phases des réseaux L2 : du zéro à un puis à deux, la sécurité déterminée par la gouvernance
Les trois phases de sécurité des rollups Ethereum peuvent être définies selon le moment où le comité de sécurité peut outrepasser les composants sans confiance (c’est-à-dire purement cryptographiques ou basés sur la théorie des jeux) :
-
Phase 0 : Le comité de sécurité dispose d’un contrôle total. Un système de preuve peut être opérationnel (Optimism ou ZK), mais le comité de sécurité peut le contrecarrer par une simple majorité. Le système de preuve est donc uniquement « consultatif ».
-
Phase 1 : Le comité de sécurité nécessite une approbation de 75 % (au moins 6 sur 8) pour outrepasser le système en cours. Un quorum bloquant doit exister en dehors des organisations principales (par exemple ≥ 3). Ainsi, prendre le contrôle du système de preuve devient relativement difficile, bien que non impossible.
-
Phase 2 : Le comité de sécurité ne peut agir qu’en cas d’erreur prouvée. Une erreur prouvée pourrait par exemple consister en une contradiction entre deux systèmes redondants de preuves (OP et ZK). En présence d’une telle erreur, il ne peut choisir qu’entre les réponses proposées : il ne peut pas répondre arbitrairement à un mécanisme donné.
Nous pouvons représenter graphiquement la « part de vote » détenue par le comité de sécurité à chaque phase :
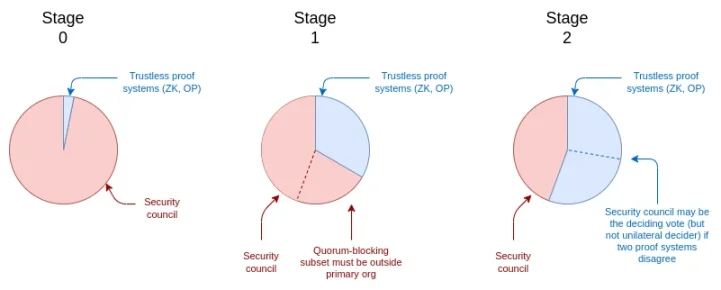
Structure de vote de gouvernance des trois phases
Une question importante se pose : quel est le moment optimal pour passer de la phase 0 à la phase 1, puis de la phase 1 à la phase 2 ?
La seule justification valable pour ne pas entrer immédiatement en phase 2 est de ne pas faire entièrement confiance au système de preuve — une préoccupation compréhensible : ce système repose sur une grande quantité de code, et si celui-ci contient une faille, un attaquant pourrait voler tous les actifs des utilisateurs. Plus votre confiance dans le système de preuve est élevée (ou inversement, plus votre confiance dans le comité de sécurité est faible), plus vous aurez intérêt à pousser l’écosystème vers la phase suivante.
En réalité, nous pouvons quantifier cela grâce à un modèle mathématique simplifié. Établissons d’abord nos hypothèses :
-
Chaque membre du comité de sécurité a une probabilité de 10 % de « défaillance individuelle » ;
-
Nous considérons comme équiprobables les pannes de vivacité (refus de signer ou clés indisponibles) et les pannes de sécurité (signature d’éléments erronés ou clés compromises). En pratique, nous postulons une catégorie unique de « panne », où un membre défaillant du conseil de sécurité signe des éléments incorrects et ne parvient pas à signer ceux qui sont corrects ;
-
Dans la phase 0, le seuil de décision du comité de sécurité est de 4 sur 7 ; dans la phase 1, de 6 sur 8 ;
-
Nous supposons un système de preuve unique global (contrairement à un mécanisme de type 2/3, où le comité de sécurité pourrait trancher en cas de désaccord). Ainsi, en phase 2, la présence du comité de sécurité devient fondamentalement sans effet.
Sous ces hypothèses, visant à minimiser la probabilité de panne du réseau L2 en fonction d’une probabilité donnée de panne du système de preuve,
Nous pouvons utiliser la distribution binomiale :
-
Si chaque membre du comité de sécurité a 10 % de chance de défaillance indépendante, alors la probabilité que 4 membres sur 7 au moins tombent en panne est ∑𝑖=47(7 𝑖)∗0.1𝑖∗0.97−𝑖 = 0.002728. Ainsi, le système intégré en phase 0 présente une probabilité fixe de panne de 0,2728 %.
-
Le système intégré en phase 1 peut également échouer si le système de preuve tombe en panne et que le mécanisme de validation du comité connaît ≥ 3 défaillances, empêchant la couverture du calcul réseau (probabilité ∑𝑖=38(8 𝑖)∗0.1𝑖∗0.98−𝑖 = 0.03809179 multipliée par le taux de panne du système de preuve), ou si le comité connaît 6 défaillances ou plus, lui permettant d’imposer seul une réponse de calcul erronée (probabilité fixe ∑𝑖=68(8 𝑖)∗0.1𝑖∗0.98−𝑖 = 0.00002341) ;
-
La probabilité de panne du système fusionné en phase 2 est identique à celle du système de preuve.
Ce qui donne le graphique suivant :
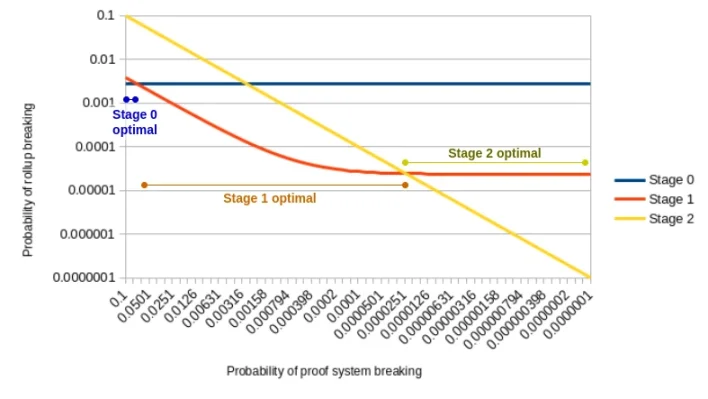
Probabilité de panne du système de preuve selon les phases du réseau L2
Comme indiqué ci-dessus, à mesure que la qualité du système de preuve s'améliore, la meilleure phase passe de la phase 0 à la phase 1, puis de la phase 1 à la phase 2. Utiliser un système de preuve de qualité phase 0 dans un réseau fonctionnant en phase 2 donne le pire résultat possible.
Maintenant, notons que les hypothèses du modèle simplifié ci-dessus ne sont pas parfaites :
-
Dans la réalité, les membres du comité de sécurité ne sont pas totalement indépendants : ils peuvent présenter des « défaillances communes » (conspiration, coercition ou piratage simultané, etc.). L'exigence d'un sous-ensemble bloquant en dehors des organisations principales vise à éviter cela, mais reste imparfaite.
-
Le système de preuve lui-même peut être composé de plusieurs systèmes indépendants (comme je l'ai recommandé dans un précédent billet). Dans ce cas, (i) la probabilité de panne du système de preuve devient très faible, et (ii) même en phase 2, le comité de sécurité reste important car il joue un rôle clé dans la résolution des conflits.
Ces deux arguments montrent que les phases 1 et 2 sont plus attrayantes que ne le suggère le graphique.
Si vous suivez la logique mathématique, la justification de la phase 1 apparaît presque toujours infondée : vous devriez passer directement à la phase 2. L’objection principale que j’entends est la suivante : en cas d’erreur critique, il pourrait être difficile d’obtenir rapidement les signatures de 6 membres sur 8 du comité de sécurité pour y remédier. Mais une solution simple existe : accorder à tout membre du comité de sécurité le droit de retarder les retraits de 1 à 2 semaines, offrant ainsi aux autres suffisamment de temps pour intervenir.
En revanche, sauter trop tôt en phase 2 serait une erreur, surtout si ce passage se fait au détriment du renforcement du système de preuve sous-jacent. Idéalement, des fournisseurs de données comme L2Beat devraient afficher des indicateurs d’audit et de maturité du système de preuve (de préférence au niveau de l’implémentation du système de preuve plutôt que du rollup entier, afin de permettre la réutilisation), accompagnés de l’indication de la phase.
Bienvenue dans la communauté officielle TechFlow
Groupe Telegram :https://t.me/TechFlowDaily
Compte Twitter officiel :https://x.com/TechFlowPost
Compte Twitter anglais :https://x.com/BlockFlow_News
















