FOAKS에서 다항식 커밋 프로토콜 Brakedown 이해하기
TechFlow 선정TechFlow 추천
FOAKS에서 다항식 커밋 프로토콜 Brakedown 이해하기
암호학자들이 텐서 곱(Tensor Product)과 다항식 평가 사이의 연관성을 발견하지 못했다면, 다항식 약속 프로토콜 Brakedown이 등장하기 어려웠을 것이며, Brakedown을 기반으로 한 Orion 및 FOAKS의 탄생도 불가능했을 것이다.
Web3 심층 보도에 집중하고 흐름을 통찰저자: Fox Tech CEO 강수열, Fox Tech 수석 과학자 몽현제
서론: 만약 암호학자들이 텐서곱(Tensor Product)과 다항식 평가 사이의 관계를 발견하지 못했다면, 다항식 커밋 프로토콜인 Brakedown은 등장하기 어려웠을 것이며, Brakedown 기반의 Orion 및 FOAKS와 같은 새로운 고속 알고리즘도 탄생하지 못했을 것이다.
다양한 다항식 커밋을 활용하는 제로지식 증명 시스템에서 서로 다른 커밋 프로토콜이 사용된다. a16z의 저스틴 탈러(Justin Thaler)가 2022년 8월에 발표한 "Measuring SNARK performance: Frontends, backends, and the future"라는 논문에 따르면, Brakedown은 증명 크기는 상대적으로 크지만 현재 가장 빠른 다항식 커밋 프로토콜임이 입증되었다.
FRI, KZG, Bulletproof은 더 일반적인 다항식 커밋 프로토콜이지만 속도 면에서 병목 현상이 발생한다. zkSync가 채택한 Plonky, Polygon zkEVM이 채택한 Plonky 2, Scroll이 채택한 Ultra-Plonk 등의 알고리즘은 모두 KZG 기반의 다항식 커밋을 사용한다. 증명자는 다항식 생성 및 커밋을 위해 대규모 FFT 계산과 MSM 연산을 수행해야 하며, 이 두 가지는 모두 막대한 계산 부담을 초래한다. MSM은 다중 스레드 가속화 가능성이 있지만 많은 메모리를 필요로 하며, 고도의 병렬 처리에서도 느리고, 큰 규모의 FFT는 알고리즘 실행 중 데이터의 빈번한 재정렬에 크게 의존하여 분산 처리를 통해 여러 컴퓨팅 클러스터에 걸쳐 가속화하기 어렵다.
바로 이러한 이유로 인해 보다 빠른 다항식 커밋 프로토콜인 Brakedown이 등장하면서 해당 연산의 복잡도가 크게 감소하게 되었다.
FOAKS(Fast Objective Argument of Knowledges)는 Fox Tech에서 제안한 Brakedown 기반의 제로지식 증명 시스템 프레임워크이다. FOAKS는 Orion의 기반 위에서 FFT 연산을 더욱 줄였으며 궁극적으로는 FFT를 완전히 제거하는 것을 목표로 한다. 또한 FOAKS는 증명 크기를 줄이기 위해 매우 정교한 새로운 형태의 증명 재귀 방식을 설계하였다. FOAKS 프레임워크의 장점은 선형 증명 시간을 실현하면서도 비교적 작은 증명 크기를 갖는 것으로, zkRollup 시나리오에 매우 적합하다.
아래에서는 FOAKS가 사용하는 다항식 커밋 프로토콜인 Brakedown에 대해 자세히 설명하겠다.
암호학에서 커밋(Commitment) 프로토콜이란 증명자가 특정 비밀 값을 커밋하여 공개 가능한 커밋 값을 생성하는 것을 말하며, 이 커밋 값은 바인딩성(Binding)과 은닉성(Hiding)을 가져야 한다. 이후 제출자는 이 커밋을 공개하고 검증자에게 메시지를 전송하여 커밋과 메시지 간의 일치 여부를 검증받는다. 이러한 점에서 커밋 프로토콜은 해시 함수와 유사한 역할을 하지만, 일반적으로 공개키 암호학의 수학적 구조에 기반을 둔다. 다항식 커밋(Polynomial Commitment)은 다항식 자체를 커밋 대상으로 하는 커밋 방식이며, 주어진 지점에서 다항식 값을 산출하고 이를 증명하는 알고리즘을 포함하므로 중요한 암호학 프로토콜로서 다양한 제로지식 증명 시스템의 핵심 요소가 된다.
최근 암호학 연구에서는 텐서곱(Tensor Product)과 다항식 평가 사이의 관계가 발견됨에 따라 관련된 일련의 다항식 커밋 프로토콜이 등장하였으며, 그 대표적인 예가 Brakedown이다.
Brakedown 프로토콜의 세부 사항을 자세히 설명하기 전에, 먼저 선형 코드(Linear Code), 충돌 저항 해시 함수(Hash Function), 머클 트리(Merkle Tree), 텐서곱(Tensor Product) 연산, 그리고 다항식 평가의 텐서곱 표현에 대한 기초 지식을 이해할 필요가 있다.
첫째, 선형 코드(Linear Code)에 대해 살펴보자. 길이 k의 메시지를 길이 n의 코드워드로 변환하는 선형 코드는 Fⁿ 내의 선형 부분공간
C ⊂ Fⁿ이며, 메시지에서 코드워드로의 단사 함수, 즉 인코딩 함수 EC: Fᵏ → C가 존재한다. 임의의 코드워드들의 선형 조합 역시 유효한 코드워드가 된다. 두 코드워드 u, v의 거리는 그들의 해밍 거리로 정의되며 △(u, v)로 표기한다.
최단 거리는 d = minu,v△(u, v)로 정의되며, 이러한 코드를 [n, k, d] 선형 코드라 하고, 상대적 최단 거리는 d/n으로 나타낸다.
둘째, 충돌 저항 해시 함수(Hash Function)와 머클 트리(Merkle Tree)에 대해 알아본다.
H: {0, 1}2λ → {0, 1}λ를 하나의 해시 함수로 표기하자. 머클 트리는 특수한 자료구조로서 2d개의 메시지를 커밋하여 하나의 해시값 h를 생성하며, 임의의 메시지를 공개할 때에는 d+1개의 해시값을 제공하면 된다.
머클 트리는 깊이 d인 이진 트리로 표현할 수 있으며, L개의 메시지 원소 m₁, m₂, ..., mL는 각각 트리의 리프 노드에 대응된다. 트리의 모든 내부 노드는 두 자식 노드의 해시값을 결합하여 계산된다. 메시지 mi를 공개할 때는 mi에서 루트 노드까지의 경로를 공개해야 한다.
다음과 같은 표기법을 사용한다:
-
h ← Merkle.Commit(m₁, ..., mL)
-
(mi, πi) ← Merkle.Open(m, i)
-
{0, 1} ← Merkle.Verify(πi, mi, h)
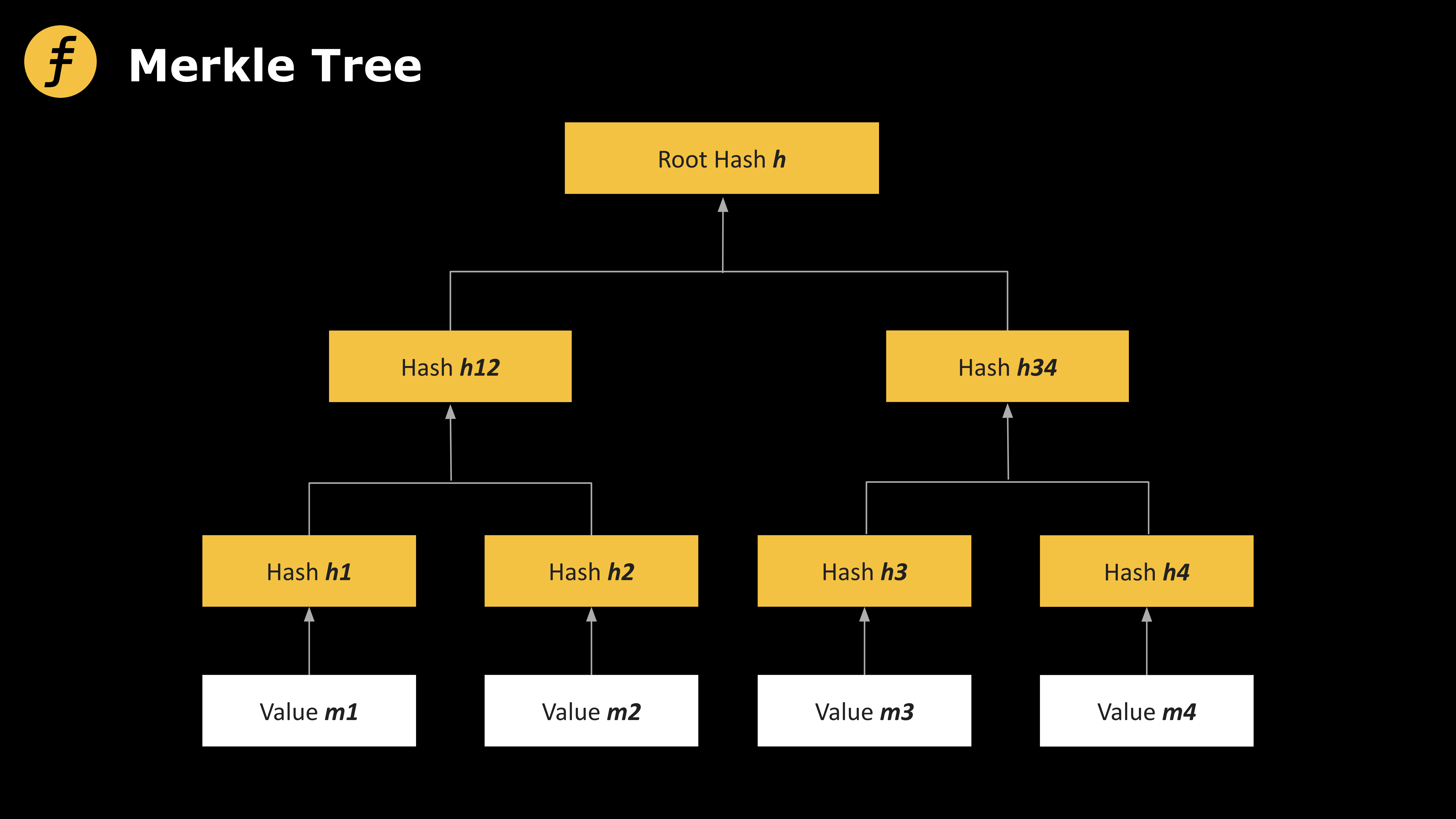
그림 1: 머클 트리(Merkle Tree)
텐서곱(Tensor Product) 연산에 대해서도 이해해야 한다. 수학적으로 텐서는 벡터와 행렬을 고차원 공간으로 확장한 개념으로, 중요한 연구 대상이지만 본문의 범위를 넘어서므로 여기서는 벡터와 행렬의 텐서곱 연산만 소개한다.
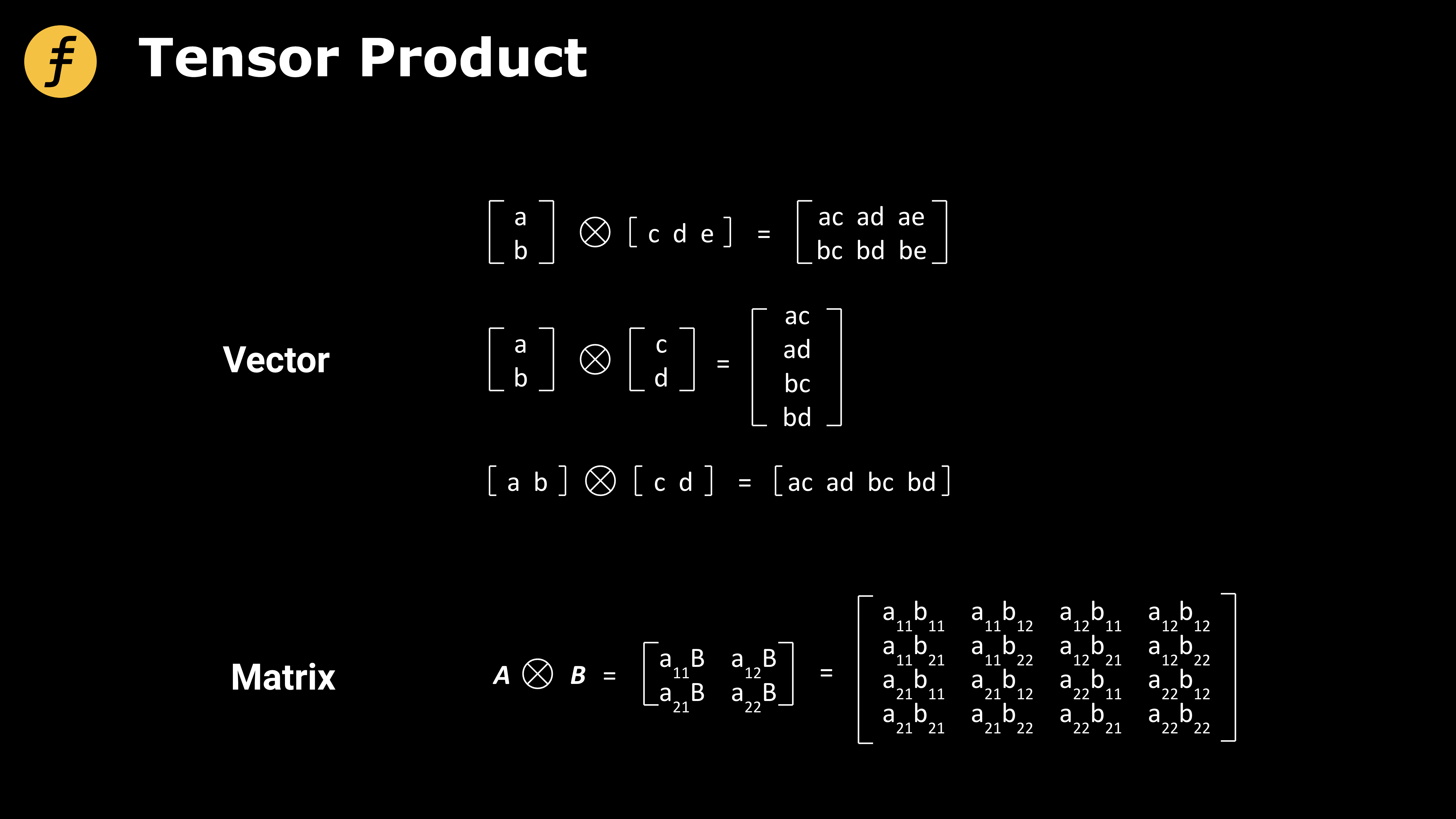
그림 2: 벡터와 행렬의 텐서곱 연산
이어서 다항식 평가의 텐서곱 표현을 알아야 한다.
[GLS+]에 따르면, 다항식의 평가값은 텐서곱 형태로 표현될 수 있다. 여기서는 다중선형 다항식의 커밋을 고려한다.
구체적으로, 주어진 다항식이 벡터 x₀, x₁, ..., xlogN-1에서의 평가값은 다음과 같이 쓸 수 있다:
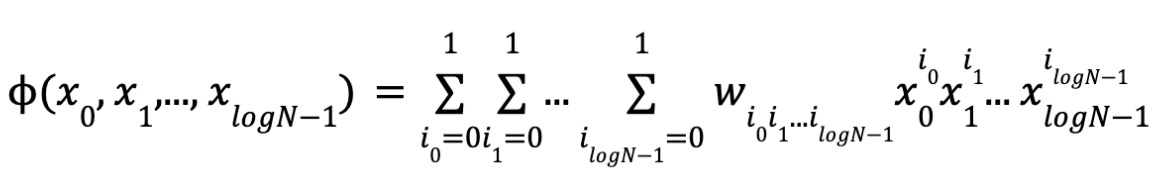
다중선형성의 정의에 따라 각 변수의 차수는 0 또는 1이므로, N개의 단항식과 계수, logN개의 변수가 존재한다. 여기서
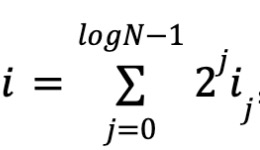
이며, i₀i₁...ilogN-1은 i의 이진 표현이다. w를 다항식의 계수 벡터라 하자.
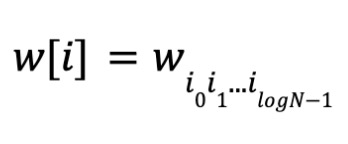
마찬가지로,
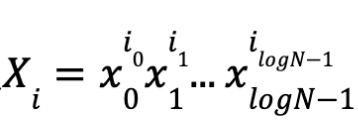
를 정의하자.
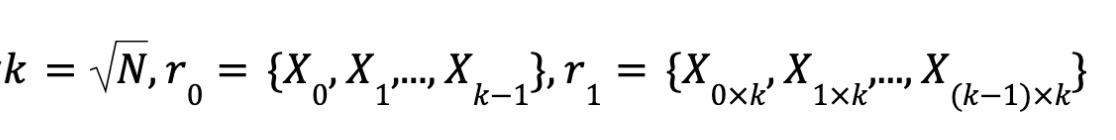
그러면 X = r₀ ⊗ r₁이 성립한다.
따라서 다항식의 평가값은 텐서곱 형태로 표현된다: ϕ(x₀, x₁, ..., xlogN-1) = ⟨w, r₀ ⊗ r₁⟩.
마지막으로, FOAKS와 Orion[XZS 22]에서 사용되는 Brakedown 프로토콜의 절차를 살펴보자.
먼저 PC.Commit은 다항식 계수 w를 k×k 행렬 형태로 나누고, 이를 선형 코드로 인코딩(“예비 지식” 참조)하여 C₂라고 표기한다. 이후 C₂의 각 열 C₂[:, i]에 대해 머클 트리를 구성하고, 각 열의 머클 트리 루트들로부터 또 다른 머클 트리를 구성하여 최종 커밋값으로 사용한다.
평가값 증명 과정에서는 두 가지를 증명해야 한다: 근접성(Proximity)과 일관성(Consistency). 근접성은 커밋된 행렬이 실제로 인코딩된 코드워드와 충분히 근접함을 보장하며, 일관성은 y = ⟨w, r₀ ⊗ r₁⟩임을 보장한다.
근접성 검증: 근접성 검증은 두 단계로 이루어진다. 먼저 검증자가 무작위 벡터 Y₀를 증명자에게 전달하면, 증명자는 Y₀와 C₁의 내적을 계산하여, 즉 Y₀의 성분을 계수로 하여 C₁의 행에 대한 선형 조합을 수행한다. 선형 코드의 성질에 따라 CY₀는 YY₀의 코드워드가 된다. 이후 증명자는 CY₀가 커밋된 코드워드로부터 계산되었음을 입증해야 한다. 이를 위해 검증자는 무작위로 t개의 열을 선택하고, 증명자는 해당 열들을 공개하며 머클 트리 증명을 제공한다. 검증자는 이들 열과 Y₀의 내적이 CY₀의 해당 위치와 일치하는지 확인한다. [BCG 20]에서는 사용된 선형 코드의 상대적 거리가 상수일 경우, 커밋된 행렬이 압도적인 확률로 어떤 코드워드에 근접함을 증명하였다(압도적인 확률이라 함은 명제의 부정이 성립할 확률이 무시할 수 있을 정도로 작다는 의미).
일관성 검증: 일관성 검증은 근접성 검증과 유사한 절차를 따른다. 차이점은 무작위 벡터 Y₀ 대신 직접 r₀를 사용하여 선형 조합을 수행한다는 점이다. 마찬가지로 c₁은 메시지 y₁의 선형 코드이며,
ϕ(x) = ⟨y₁, r₁⟩이 성립한다. [BCG 20]에서는 일관성 검증을 통과하면, 커밋된 행렬이 코드워드에 근접할 경우 압도적인 확률로 y = ϕ(x)가 성립함을 증명하였다.
의竊코드 형식으로 Brakedown 프로토콜의 절차를 제시하면 다음과 같다:
공개 입력: 평가 지점 X. 텐서곱 X=r₀⊗r₁로 파싱됨.
비공개 입력: 다항식 ϕ, 그 계수를 w로 표기.
C를 [n, k, d]-선형 코드라 하고, EC: Fᵏ→Fⁿ을 인코딩 함수라 하자. N=k×k. N이 완전제곱수가 아닐 경우 다음 완전제곱수까지 패딩할 수 있다. Python 스타일 표기법 mat[:, i]를 사용하여 행렬 mat의 i번째 열을 선택한다.
-
함수 PC.Commit(ϕ):
-
w를 k×k 행렬로 파싱한다. 증명자가 로컬에서 텐서 코드 인코딩 C₁, C₂를 계산한다. C₁은 k×n 행렬, C₂는 n×n 행렬이다.
-
for i ∈ [n] do
-
머클 트리 루트 Rooti = Merkle.Commit(C₂[:, i])를 계산한다.
-
머클 트리 루트 R = Merkle.Commit([Root₀, ..., Rootn-1])를 계산하고, R을 커밋값으로 출력한다.
-
함수 PC.Prover(ϕ, X, R)
-
증명자는 검증자로부터 무작위 벡터 Y₀ ∈ Fᵏ를 수신한다.
-
근접성 (Proximity)
-
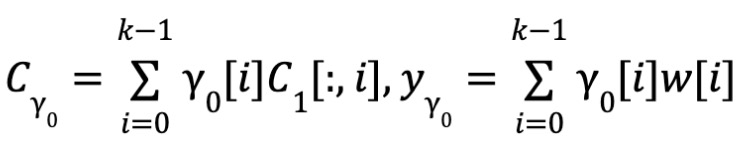
일관성 (Consistency)
-
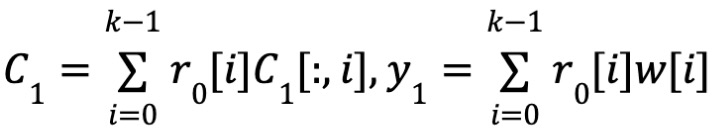
증명자가 C₁, y₁, C₀, y₀를 검증자에게 전송한다.
-
검증자가 t[n]에서 배열 Î를 무작위로 샘플링하여 증명자에게 전송한다.
-
for idx ∈ Î do
-
증명자가 C₁[:, idx]와 R 아래에서 C₂[:, idx]에 대한 Rootidx의 머클 트리 증명을 검증자에게 전송한다.
-
함수 PC.VERIFY_EVAL(π, X, y=ϕ(X), R)
-
근접성: ∀idx ∈ Î, CY₀[idx] == ⟨Y₀, C₁[:, idx]⟩이고 EC(YY₀) == CY₀
-
일관성: ∀idx ∈ Î, C₁[idx] == ⟨Y₀, C₁[:, idx]⟩이고 EC(Y₁) == C₁
-
y == ⟨r₁, y₁⟩
-
∀idx ∈ Î, EC(C₁[:, idx])가 ROOTidx와 일치하고, ROOTidx의 머클 트리 증명이 유효하다.
-
위의 모든 조건이 만족하면 수락, 그렇지 않으면 거부.
결론: 다항식 커밋은 제로지식 증명 시스템을 포함한 다양한 암호학 시스템에서 널리 사용되는 매우 중요한 암호학 프로토콜이다. 본문에서는 다항식 커밋 프로토콜 Brakedown과 관련 수학 지식을 자세히 설명하였으며, FOAKS의 중요한 하부 구성 요소로서 Brakedown은 FOAKS의 구현 성능 향상에 중요한 역할을 하였다.
참고문헌
-
[GLS+]: Alexander Golovnev, Jonathan Lee, Srinath Setty, Justin Thaler, Riad S. Wahby. Brakedown: Linear-time and post-quantum snarks for r1cs. Cryptology ePrint Archive. https://ia.cr/2021/1043.
-
[XZS 22]: Xie T, Zhang Y, Song D. Orion: Zero knowledge proof with linear prover time[C]//Advances in Cryptology–CRYPTO 2022: 42nd Annual International Cryptology Conference, CRYPTO 2022, Santa Barbara, CA, USA, August 15–18, 2022, Proceedings, Part IV. Cham: Springer Nature Switzerland, 2022: 299-328. https://eprint.iacr.org/2022/1010
-
[BCG 20]: Bootle, Jonathan, Alessandro Chiesa, Jens Groth. "Linear-time arguments with sublinear verification from tensor codes." Theory of Cryptography: 18th International Conference, TCC 2020, Durham, NC, USA, November 16–19, 2020, Proceedings, Part II 18. Springer International Publishing, 2020.
-
A16z crypto 소속 저스틴 탈러, Measuring SNARK performance: Frontends, backends, and the future https://a16z crypto.com/measuring-snark-performance-frontends-backends-and-the-future/
-
텐서곱 소개: https://blog.csdn.net/chenxy_bwave/article/details/127288938
TechFlow 공식 커뮤니티에 오신 것을 환영합니다
Telegram 구독 그룹:https://t.me/TechFlowDaily
트위터 공식 계정:https://x.com/TechFlowPost
트위터 영어 계정:https://x.com/BlockFlow_News
