なぜギャンブル依存は最終的にすべてを失うのか?非遍历性システムにおける生存法則
TechFlow厳選深潮セレクト

なぜギャンブル依存は最終的にすべてを失うのか?非遍历性システムにおける生存法則
いつでももう一回やれば巻き返せる気がするのも、集団の平均値を個々の運命と誤認しているからに他ならない。
著者:雪鵝、DataCafe

1000元の初期資金を持って、このようなコイントス・チャレンジゲームに参加すると想像してみてください。あなたはいつまでも続けたいと思えるかもしれません。
毎ラウンド、コインを1回投げます。
表が出れば、資産が80%増加します。
裏が出れば、資産が50%減少します。
どう見ても、絶対に損しないゲームに思えます!
しかし現実は……
10万人のプレイヤーにこのゲームを100回ずつプレイさせると、平均資産は確かに指数関数的に増加するものの、大多数の人の最終的な資産はわずか72元以下にまで落ち込み、破産してしまうのです。
なぜ平均資産は増えているのに、ほとんどの人はどんどん貧しくなってしまうのでしょうか?
これが典型的な「非遍歴性(ノンエルゴディック)」のワナです。もう一回やれば取り返せるはずだと常に思い続けるのは、集団の平均値を自分の運命と誤って同一視しているからです。
非遍歴性の罠:長期平均 ≠ あなたの真の運命
では、遍歴性とは何でしょうか?
「遍歴性(Ergodicity)」という概念はもともと統計物理学に登場し、確率論、金融、行動科学、機械学習などの分野にも大きな影響を与えています。その核心は、「長期平均値が個人に適用できるのか?」という問いです。意思決定を行う際、私たちは「長期平均」を信じるべきなのか、それとも「一回一回の体験」を重視すべきなのか?
19世紀、物理学者ルートヴィヒ・ボルツマン(Ludwig Boltzmann)は気体分子の運動を研究する中で、遍歴性仮説を提唱しました。十分長い時間観察すれば、ある一つの気体分子はあり得るすべての状態を通り抜けるというものです。
密閉された容器内の気体を想像してみてください。無数の分子が衝突を繰り返しながら、それぞれ異なる速度の軌道を描いています。個々の分子の長期的軌道と、全体の気体の統計的分布が一致するならば、ある瞬間における全分子の状態から、単一分子の長期的振る舞いを推測できるということです。
これが有名なボルツマンの遍歴性仮説です。

数学的には、遍歴性とは次を意味します:
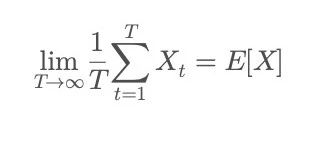
左側は時間平均:ある個人が非常に長い時間をかけて同じプロセスを繰り返した結果の平均値を示しています。
右側は集団平均:ある瞬間に無数の個人を観察して得られる統計的期待値です。つまり、システムが遍歴性を持つ場合、個人の結果は最終的に集団の「長期平均」に収束するということです。
もし世界が遍歴的であれば、誰もが最終的に社会の平均的な富水準に近づくでしょう。遍歴的な世界では、誰もが豊かさ・貧しさ・成功・失敗といったあらゆる経済状態を経験でき、個人の運命は必ずや集団の「長期平均」へと収束します。
しかし現実の世界は往々にして非遍歴的です。個人の資源は限られており、すべての可能性を経験する前に、一度の失敗によって完全に脱落してしまうことがよくあります。
私たちは次のような、導きやすい主張をよく耳にします。
「ある業界の平均年収は100万円を超えている」
「ある人は30歳で財務的に自由になり、起業してわずか2年で成功した」
「あるインデックスファンドは長期的に高い年率リターンを記録しており、継続投資すれば必ず豊かになれる」
……
こうした一見理にかなった統計データは、まるで確かな真実を語っているかのように感じられます。行動さえすれば、長期平均の恩恵が個人にも適用されると錯覚してしまいます。しかし、これらの事例はパス依存性が強く、再現不可能な非遍歴的プロセスにすぎません。模倣者は同じ歴史的背景、人脈、幸運のタイミングを持ち合わせておらず、隠れた失敗者の数も把握できません。
データは集団の長期平均を教えてくれますが、現実には短期間で訪れる「断崖的失敗」が満ちています。
これが非遍歴性が仕掛ける最も巧妙な罠です――ビッグデータの平均値 ≠ 個人の真の運命。
個人にとって一度の崩壊は取り返しがつかず、一度の失敗で人生から完全に脱落し、「平均状態」に戻れなくなることがあります。私たち一人ひとりの人生の軌跡は一度しか歩めず、カジノのように多数の賭け手の中で確率が平均化されるような集団的長期平均を享受することはできません。
なぜ個人の長期的運命は「平均値」よりも劣るのか?
非遍歴的システムにおいて、個人の長期的成果はしばしば集団平均を下回ります。これは偶然ではなく、構造的な特徴です。華やかな平均値は、ごく少数の起業成功者、投資での急騰、逆境からの這い上がりといった物語によって押し上げられており、多くの失敗者はそもそも統計に含まれていません。
現実のシステムは大抵の場合乗法型であり、パス依存性を持つ特徴があります。たとえば投資の複利、健康の劣化、評判の毀損などです。こうしたシステムの典型的な特徴は上昇は限定的だが、下降には底がないことです。
一度の破産が人生を台無しにするかもしれない。
一度の誤った判断が運命を完全に変えるかもしれない。
一度の信頼違反で信用が完全に失われるかもしれない。
一方で、得られる富、上がるパフォーマンス、築ける優位性は常に限られています。
そのため数学的に言えば、乗法型プロセスの長期成長率は「平均リターン」と等しくないのです。むしろ次に近くなります:
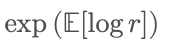
一方、集団平均は通常算術平均を使います。
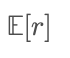
そして対数関数は厳密な凹関数であるため、ジェンセンの不等式により次の関係が成り立ちます:
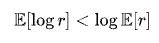
したがって、乗法型システムの長期成長率(すなわち幾何平均)は常に算術平均より小さくなります。変動が大きいほど、この差は顕著になります。算術平均は「永遠に幸運ならどうなるか」を教え、幾何平均は「現実世界を乗り越えた後に残るのは何か」を教えてくれます。
つまり個人の長期的成果が「集団平均リターン」を大きく下回るのは、運が悪いからではなく、構造上の必然なのです。
最適な意思決定とは? ケリー基準の黄金分割点
では人生の意思決定において、長期的なゲームでゼロになる運命を避けるために何ができるでしょうか?破産せずに、かつ長期的な複利を得るには?
答えはこれです:決してAll inせず、ケリーベットを学びましょう!
ケリー基準(Kelly Criterion)とは繰り返し行うゲームにおける最適な賭け戦略であり、短期的な破産を避けながら長期リターンを最大化することを目的としています。この理論はジョン・ケリー・ジュニア(John L. Kelly Jr.)が1956年にベル研究所で提唱したもので、当初は「ノイズのある通信路で信号電力をどのように配分すれば情報伝送効率を最大化できるか」という問題を解決するために考案されました。
その後、この理論はすぐに他分野へと広がりました。
アメリカの数学者で投資の天才エドワード・ソープ(Edward Thorp)は、ケリー基準が富の成長経路を最適化できることに気づきました。彼はこれをカジノに持ち込み、『ブラックジャックを打ち負かす』(Beat the Dealer)で初めて21対1のディーラーに体系的に勝利した後、ウォール街に応用し、『マーケットを打ち負かす』(Beat the Market)でさらなる成功を収めました。
この基準の本質は、対数期待効用(log-utility)を最大化することで、成長とリスクの動的バランスを両立させることにあります。つまり、「長く生き延びる」ことと「しっかり稼ぐ」ことの最適なバランスポイントを見つけてくれるのです。
ケリー公式:
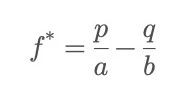
ここで、成功確率を p、失敗確率を q = 1-p とし、成功時の利益倍率(元本を含まない)を b、失敗時の損失率を a とします(通常 a=1、つまり賭け金全てを失う場合)。
冒頭のコイントスゲームに戻ると、一定割合の元本を賭け続けていくことができますが、一体いくら賭けるのが最適でしょうか?
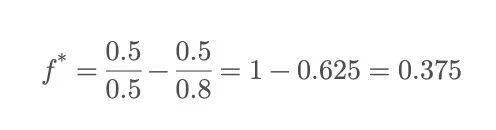
つまり、ケリー公式は総資金の37.5%を毎回投入することを推奨しています。多すぎれば、有利な条件でも連続失敗で即座に破産するリスクがあり、少なすぎれば本来得られたはずの成長を逃します。
ケリー公式の意義は、長期的に最大の利益を得つつ、生存を維持できるポイントを見つけることにあります。
補足として、ケリー公式は勝率やオッズに対して非常に敏感ですが、現実ではこれらのパラメータは不確実または動的に変化するため、多くの慎重な実践者は「半分のケリー戦略(Half-Kelly)」を採用し、より滑らかなリターン曲線を得ようとします。
シミュレーション実験:10万人のコイントス賭け、何人が「生き残れる」か?
異なる賭け戦略が個人の運命に与える影響を直感的に理解するために、私は冒頭のコイントスゲームに10万人のプレイヤーが参加するシミュレーションを行いました。合計200ラウンド、各プレイヤーは独立してプレイします。
ルールは同じまま:初期資金1000、表で+80%、裏で-50%。プレイヤーは固定の賭け比率を選べます。例えば全額(100%)、65%、37.5%などです。
結果は……100%賭けのプレイヤーはほぼ全滅!
最終的な資産は「べき乗則分布」を示し、極一部が大富豪になる一方、大多数が破産しました。
以下の4つの異なる賭け戦略における資産分布を比較します。右側に行くほど高資産者です。
a. 100%賭け:ほぼ全員が破産
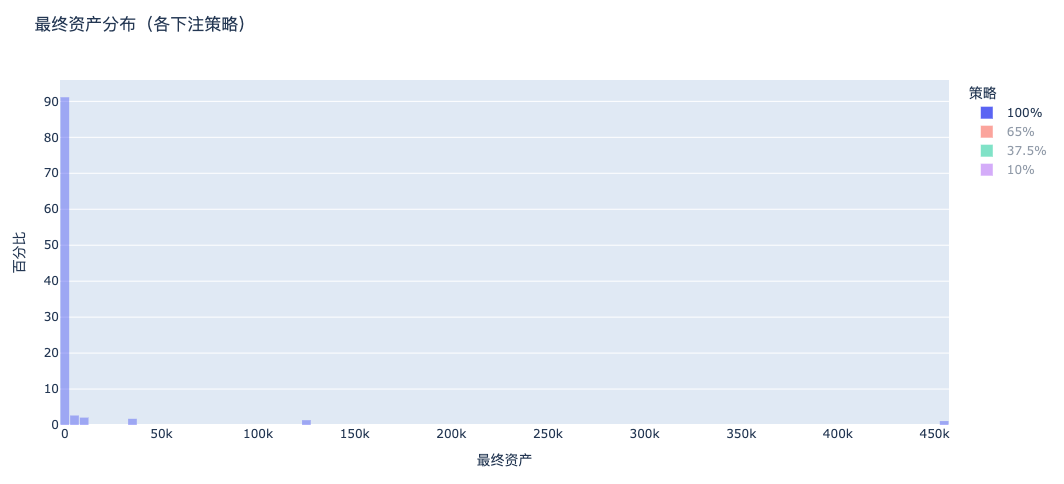
全額賭け戦略の最終資産分布は、膨大な左側の貧困ピークと、極めて細い右側の大富豪テール構造を示します。大多数が破産し、少数がすべての富を独占する――これが「不均衡なゲーム+サバイバー偏見」の真の姿です。
b. 65%賭け:依然として二極化、多数が破産
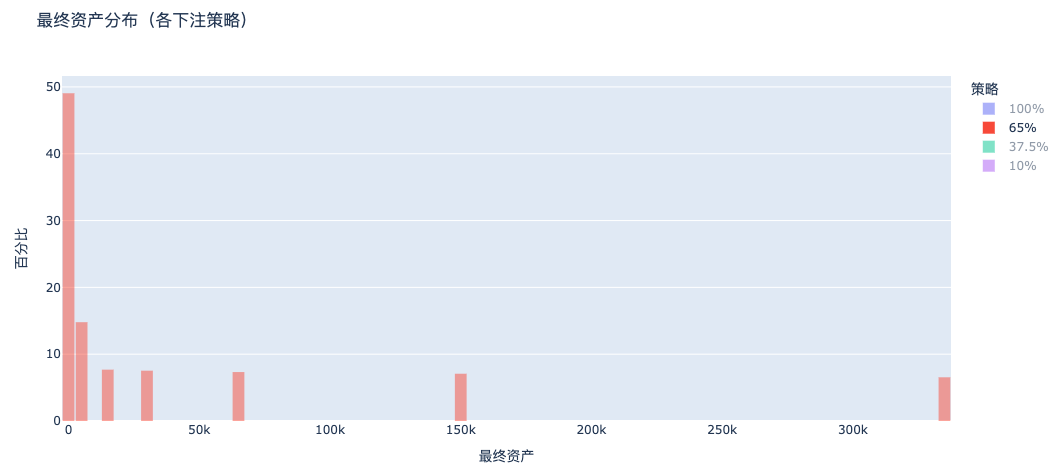
c. 37.5% 賭け(ケリー公式):資産が安定して増加
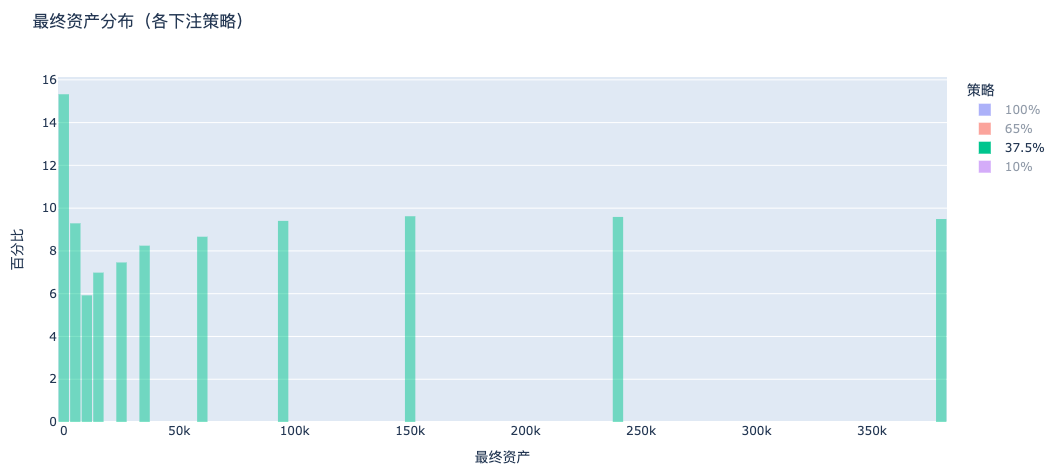
ケリー戦略では、資産分布が明確に右にシフトし、大多数の資産が増加し、分布が集中しています。これは最適な資産蓄積モデルです。
d. 10%賭け:破産者はほとんどいないがリターンが低すぎる
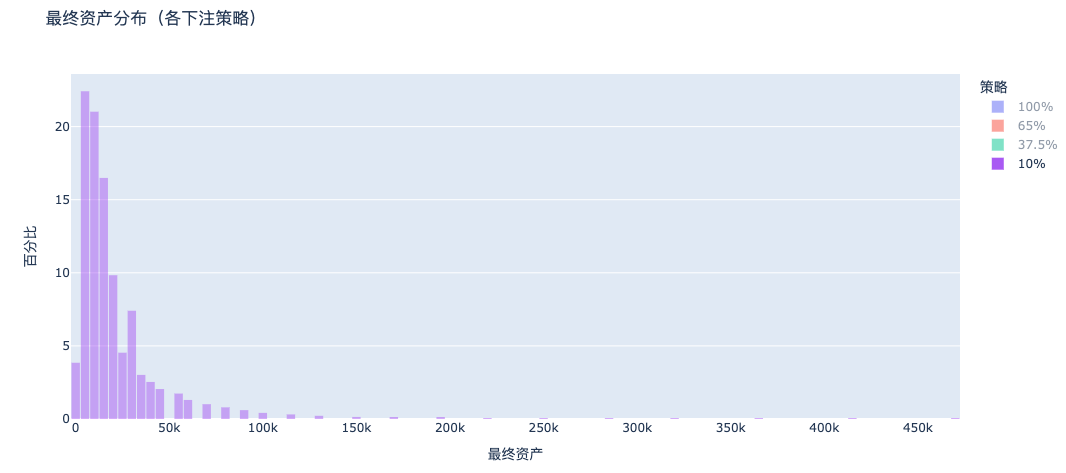
全額賭けのような破産ピークはなくなりましたが、全体の資産は低水準に集中しています。一方、37.5%戦略では右側に明確なロングテールが形成され、資産の倍増が実現されています。
ケリー戦略だけが「大多数が破産しない」と「着実な資産増加」の両方を兼ね備えており、数学的に最適な長期生存戦略です。まさにケリー公式の真髄:最大の利益を得させるのではなく、長く生き残ることを保証するのです。
ケリー公式に込められた人生哲学
ケリー公式が教えるのは、長期的成功の秘訣は「賭けの量」をどうコントロールするかにあるということです。人生は一発のクリティカルヒットを競うものではなく、最後までゲームに参加し続けることを競うものです。
職業においては、情熱だけで退職するでも、安泰な場所に固執するでもなく、着実に布石を打って能力を高め、チャンスがあれば道を変え、選択肢を常に残しておくこと。
投資においては、一発逆転を狙って全財産をかけるのではなく、オッズに応じてポジションをコントロールし、チップを残すこと。
人間関係においては、感情や価値をすべて他人に預けるのではなく、関係に投資しつつも、自分自身を保有すること。
成長と自己管理においては、一度の爆発的な努力で変化を得るのではなく、安定的かつ複利的に生活構造を最適化していくこと。
人生は長く続くゲームのようなものです。目標は一度勝つことではなく、脱落しないようにすることです。ただそこに留まり続ければ、必ず良いことが起こります。
TechFlow公式コミュニティへようこそ
Telegram購読グループ:https://t.me/TechFlowDaily
Twitter公式アカウント:https://x.com/TechFlowPost
Twitter英語アカウント:https://x.com/BlockFlow_News