Curve安定通貨設計ホワイトペーパー:継続的清算/非清算型AMM
TechFlow厳選深潮セレクト

Curve安定通貨設計ホワイトペーパー:継続的清算/非清算型AMM
提案されたメカニズムによって、ステーブルコインの発行や貸借目的でのクリアリングに伴うリスクを解決できることが望まれる。
Curve ステーブルコイン設計ホワイトペーパーの日本語対訳版。理解を助けるための注釈を追加し、原文のスペルミスも修正しています。参考・学習用としてご活用ください。
概要(Overview)
このステーブルコイン設計にはいくつか重要な概念がある。すなわち、貸出・清算AMMアルゴリズム(LLAMMA)、PegKeeper(価格安定化メカニズム)、および金融政策である。特に中心となるのはLLAMMAであり、従来の過剰担保型ローンにおける強制清算プロセスを、特殊目的のAMMで置き換えるというものだ。
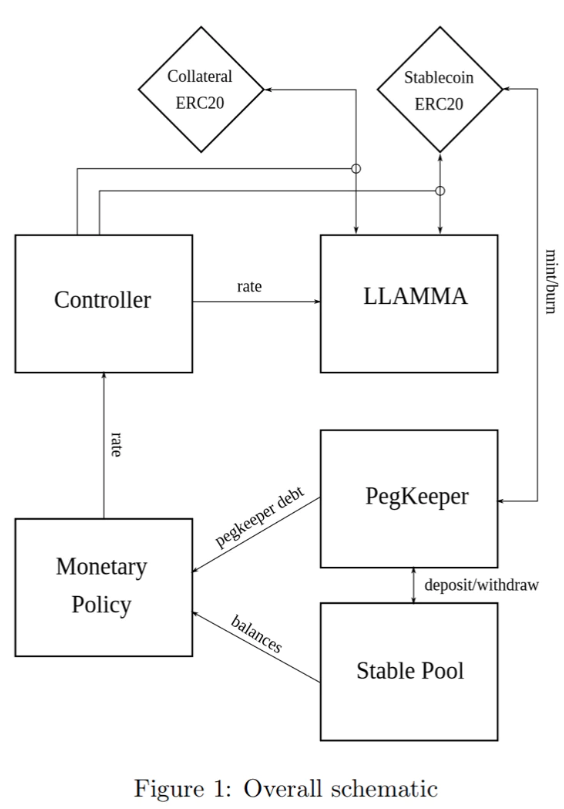
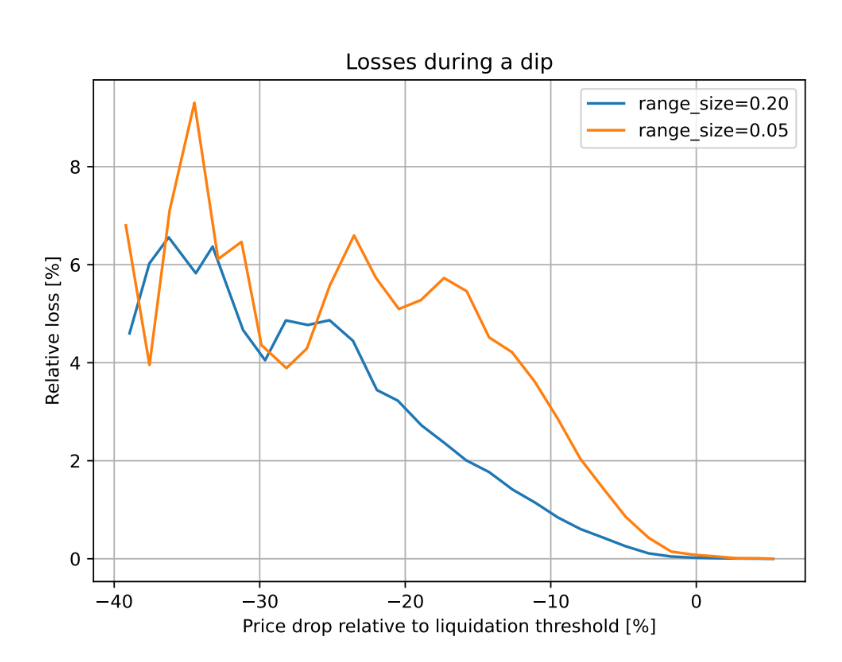
図2:清算しきい値に対する価格変動による損失の依存性。観測期間は3日間。
本設計では、担保を使って借入を行う場合、清算価格を下回った後でも価格が反発すれば、実質的な損失はほとんど発生しない。
たとえば、2017年9月以降のETH/USDの履歴データを用いたシミュレーションによると、CDPが3日間にわたり放置され、その間に価格が清算価格より10%下落する状況が発生しても、損失を被る担保はわずか1%にとどまる。
継続的清算/非清算型AMM(LLAMMA)
本ステーブルコイン設計の核心は「Lending-Liquidating AMM Algorithm(貸出・清算型AMM)」にある。 これは担保資産(例:ETH)とステーブルコイン(ここではUSDと仮称)との間の変換を行うもので、担保価格が高いときはユーザーの預入額はすべてETHとなり、価格が下落すると徐々にUSDステーブルコインへと変換されていく。これは従来のAMM設計とは大きく異なり、通常のAMMでは上部(曲線の上方)にUSD、下部(曲線の下方)にETHを配置するのに対して、本方式は外部オラクル価格に応じて動的に構成を変化させる。
以下の説明は完全に自己完結した数学的証明ではない。多くの要素(特に不変量)は複数の視点から考察された結果である。完全な数理モデルを得るにはさらなる研究が必要かもしれないが、以下に示す内容はスマートコントラクトでの実装に十分な根拠を与えると考えられる。
この機構は外部オラクルによる価格情報なしには実現できない。簡単に言えば、標準的なAMM(例えば結合曲線が双曲線であるもの)を想定し、「中心価格」が低下または上昇するにつれて、トークンが(例:USDからETHへ)断熱的に変換されながら、両方向への流動性を提供する(図3)。これは量子物理学における「回避交叉(Landau-Zener遷移)」に類似している(ただし概念的な類推であり、数学的記述は大きく異なる可能性がある)。

流動性が集中する範囲をここでは「バンド(band)」と呼ぶ。一定のオラクル価格poにおいて、pcdからpcuの範囲に流動性が存在する。ここで、pcd(po)およびpcu(po)はpoのみの関数であり、線形よりも急峻な関数、つまりpoの増加に対してより速く成長する関数を求めている(図4)。また、p↓およびp↑をそれぞれp↓(po)=po、p↑(po)=poとして、断熱極限におけるバンドの両端(例:p=po)として定義する。
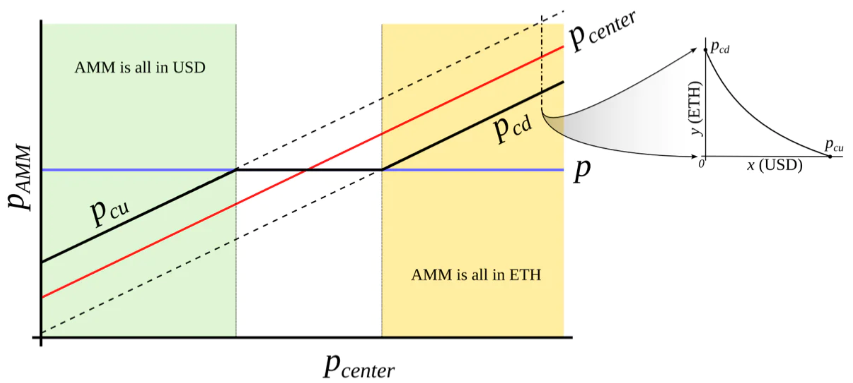
図3:「外部価格源を持つAMM」の挙動。外部価格pcenterが、流動性が集中する価格帯を決定する。AMMはpcd < pcenter < pcuの範囲に流動性を集中させ、現在価格pがpcd〜pcuの範囲外に出た場合、AMMは完全にステーブルコイン(pcu以上)または完全に担保資産(pcd以下)に切り替わる。pcd ≤ p ≤ pcuの範囲内では、AMM価格は現在価格pと等しくなる。
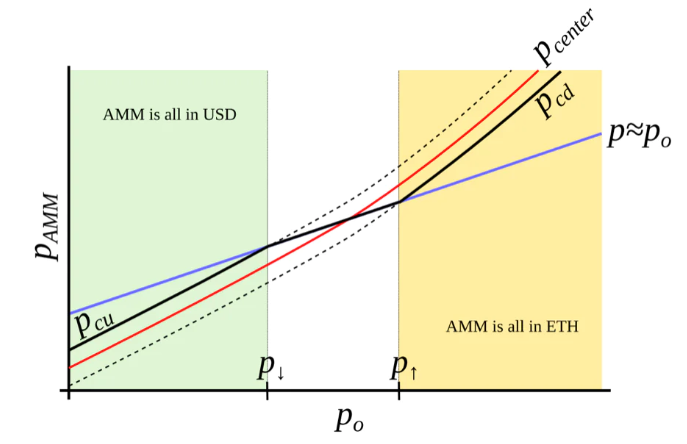
図4:我々が目指すAMM。poの増加とともにpcdおよびpcuがより急激に増加するようなAMMを構築しようとしている。これにより、ETHが高価なときはAMMがすべてETHに、安価なときはすべてUSDに変換される。
Uniswap v3と同様に、いくつかのバンドから始め、いわゆる「仮想残高」を追加することで、結合曲線の双曲線形状を維持する。USDの数量をx、ETHの数量をyとすると、「強化された」定積不変式は次のようになる:

x₀ ≡ x + f、y₀ ≡ y + gとおくことで、不変式は馴染み深い形I = x₀y₀と書ける。しかしfとgは固定値ではなく、外部オラクル価格の変化に伴って変化する(不変量Iも同様であり、オラクル価格poが一定の場合に限り「不変」である)。特定のpoにおいて、fおよびgはそのバンド内で一定である。前述の通り、p↑をバンドの上限価格、p↓を下限価格とする。ここでA(流動性集中度を示す指標)を次のように定義する:

我々が求める性質は次の通り:より高いpoでは、同じ残高でもより高い価格が得られること。つまり、現在の市場価格(平均的にはpoに追随)がその価格を下回り、バンドがETH寄りに取引されることを目指す(逆方向も同様)。これを満たす方法は多数存在するが、次のような条件を満たす必要がある:
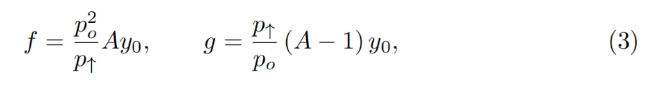
ここでy₀は、ETH建てで表した現在のバンド内預入額の尺度であり、次のように定義される:現在価格p、p↑、およびpoが一致するとき、y = y₀、x = 0となる(図4のpo = p↑の点を参照)。この瞬間のyを代入すると:

価格はdx₀/dy₀に等しいため、定積不変量では:
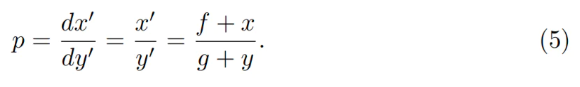
po = p↑(x=0)またはpo = p↓(y=0)の場合を代入することで、上記式の自己整合性を確認できる。
通常、あるバンドについてp↑、p↓、po、定数A、および現在の預入額x、yが既知である。その他すべてを計算するには、まずy₀を求める必要がある。これは不変式の二次方程式を解くことで得られる:
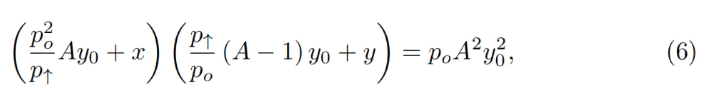
これはy₀に関する二次方程式となる:
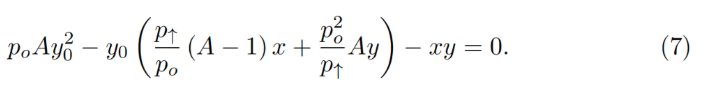
スマートコントラクトでは、get_y0関数内でこの二次方程式を解いている。
オラクル価格poが一定であれば、AMMは通常通り機能する。すなわち、価格上昇時にETHを売却し、下落時にETHを購入する。x=0を現在の下落価格pcd、またはy=0を現在の上昇価格pcuとして不変式に代入することで、現在のpoおよびp↑のもとでのAMM価格が次のように示される:
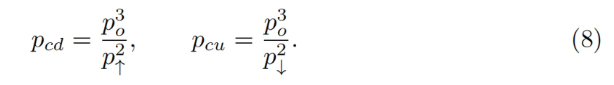
もう一つの重要な実用上の問題は、価格変動が非常に緩やかで、オラクル価格poが完全に「断熱的」に(バンド内にて)追随できる場合、初期のx、yおよびp=poから始めて、価格上昇時には最終的にどれだけのETH(y↑)が得られ、価格下落時にはどれだけのUSD(x↓)が得られるか、というものである。これは即座に解ける数学的問題ではないが、数値計算により比較的単純な答えが得られている:

これらの結果は、貸出の安全性評価およびAMMの潜在的損失分析に用いる。
以上で一つのバンドの記述が完了した。すべての価格帯を、p↓とp↑が隣接する複数のバンドに分割する。基礎価格pbaseとバンド番号nを設定すると:
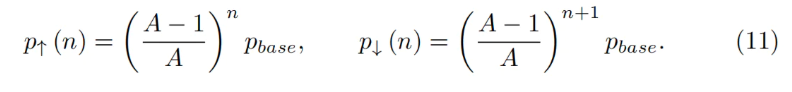
任意のバンドについて、式7および式5の解が成立することが証明できる:
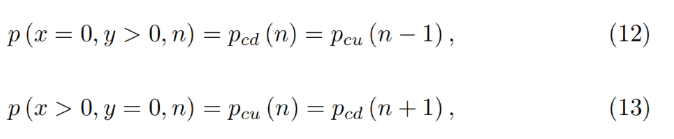
これにより、バンド間に隙間がないことが示される。
取引は式1の不変性を保ちつつ行われるが、オラクル価格poが変化すると、AMM内部の現在価格も変化する:poが下がると内部価格は上がり、逆もまた然り(立方係数)。これは式8から明らかである。
LLAMMA vs ステーブルコイン
ステーブルコインは、不安定な担保(暗号資産、例:ETH)を用いてステーブルコインを借り入れるCDPである。担保はLLAMMAの価格範囲(バンド)に投入され、担保価格が緩やかに下落すれば、ETHはCDPの返済に必要なだけのステーブルコインに変換される(自己清算、あるいは外部による清算、あるいは担保比率が危険域に近づいた場合の清算、あるいは清算せずに価格反発を待つことも可能)。
ユーザーが担保を預けステーブルコインを借り入れると、LLAMMAスマートコントラクトはその担保が属するバンドを計算する。担保価格の変動に応じて、ETHは徐々にステーブルコインに変換されていく。「水中」状態(担保不足)になると、ユーザーはすでに返済に必要なUSDを保有していることになる。取得可能なステーブルコインの量は公開関数get_x_downで計算可能である。この値が清算しきい値に極めて近い場合、外部の清算者が介入できる(ただし、担保価格が下落・横這いした数日~数週間後に発生するものであり、価格が戻らない限り決して発生しないこともある)。価格が清算水準を大幅に上回っている場合、健全な状態ではget_x_downと債務の比率に加え、担保価値の増分も反映される。
ステーブルコインが金利を受け取る場合、これはAMMにも反映されるべきである。これはすべての価格グリッドを調整することで実現される。すなわち、ステーブルコインが金利rを受け取るとき、AMM内のすべての価格グリッドは同じ率rで上方にシフトする。これは基礎価格の乗数によって達成される。したがって、受け取る金利が正であれば、乗数は時間とともに上昇していく。
get_x_downまたはget_y_upを計算する際、まず現在価格poに移動した場合のステーブルコインおよび担保の数量x*およびy*を求める。その後、poが断熱的に最低バンドの最下価格または最高バンドの最上価格まで変化した場合に、それぞれどれだけのステーブルコインまたは担保が得られるかを調べる。これにより、瞬時の現在価格に依存しない、獲得ステーブルコイン量の指標が得られ、これはフロントランニング攻撃への耐性にとって重要である。
なお、LLAMMAはETH/USD価格として定義されるpoを価格源として使用するが、当該ステーブルコインはペッグ未満(ps<1)またはペッグ超過(ps>1)で取引される可能性がある。ps<1の場合、LLAMMA内の価格pはpoより高くなる(p > po)。
断熱近似では、p = po / psとなり、すべての担保⇔ステーブルコイン変換は、より高いオラクル価格で発生する。あるいは、オラクル価格が次式のように低く見なされた場合と等価になる:
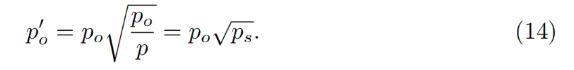
この価格において、変換時に得られるステーブルコインの量は1/ps倍多くなる(ps<1の場合)。
長期的にps>1の状態は望ましくないため、次章で述べるスタビライザーを使用する。
自動スタビライザーと金融政策
ps>1の場合(例:ステーブルコイン需要の増加)、ステーブルスワップCurveプールにおけるステーブルコインと償還可能参照通貨またはLPトークンの非対称な預入により、アンカー準備が形成される。ps>1になると、PegKeeperコントラクトは無担保でステーブルコインを新規発行し、それを単独でステーブルスワッププールに預入できる。この操作後の最終価格は依然として1以下となる。ps<1の場合は、PegKeeperが非対称的に引き出しを行い、ステーブルコインを焼却できる。
このような行動により、ps>1では価格が急速に下落し、ps<1では上昇する。非対称な預入・引き出しが価格を変化させるためである。この「鋳造」部分が無担保であっても、ステーブルコインはプール内の流動性によって暗黙のうちに担保されているように見える。全体の鋳造/焼却サイクルは最終的に利益をもたらし、同時に安定性を提供する。
スタビライザーに発行されたステーブルコイン量をdstとし、stableswap AMMのget_dx関数でステーブルコイン購入に必要な償還可能USD量を求める関数をfdx()とする。そして「準備」が極端に大きくなるのを防ぐため、「緩やかな」安定化メカニズムとして金利rの調整を行う。

ここでhはpsの変化量、rの変化率は2倍(psが高いほどrは低い)。dstの量は、ps=1かつr=r0の条件下で平衡状態に達する。したがって、dst/supplyが所定の目標値(例:5%)を超えた場合、r0を減少させ(借り手に借りてステーブルコインを売却させ、価格を下げ、システムにdstの焼却を促す)、逆に低ければr0を増加させる(借り手に返済を促しpsを押し上げ、システムにdstの増加とスタビライザー預入を促す)という動的調整が可能である(手動設定の代替として)。
まとめ
提案されたメカニズムにより、ステーブルコイン発行および貸出における強制清算リスクが解決されることを期待している。
さらに、スタビライザーおよび自動金融政策メカニズムにより、過大なPSM(Peg Stability Module:ペッグ安定化モジュール)を保持することなく価格のアンカー維持が可能となる。
TechFlow公式コミュニティへようこそ
Telegram購読グループ:https://t.me/TechFlowDaily
Twitter公式アカウント:https://x.com/TechFlowPost
Twitter英語アカウント:https://x.com/BlockFlow_News