Pourquoi l'état d'esprit du joueur mène-t-il inévitablement à tout perdre ? La loi de survie dans les systèmes non ergodiques
TechFlow SélectionTechFlow Sélection

Pourquoi l'état d'esprit du joueur mène-t-il inévitablement à tout perdre ? La loi de survie dans les systèmes non ergodiques
On a toujours l'impression qu'une partie supplémentaire permettra de renverser la situation, précisément parce que nous confondons par erreur la moyenne du groupe avec le destin individuel.
Auteur : E'gée, DataCafe

Imaginez que vous participiez à un jeu de pile ou face avec 1000 unités monétaires comme capital initial, et que vous puissiez choisir de continuer indéfiniment :
À chaque tour, on lance une pièce.
Si c’est face, votre richesse augmente de 80 %.
Si c’est pile, elle diminue de 50 %.
Ça semble être un jeu infaillible !
Mais en réalité…
Si 100 000 joueurs participent à ce jeu pendant 100 tours chacun, vous constaterez que bien que leur richesse moyenne croisse effectivement de façon exponentielle, la grande majorité d’entre eux finissent avec moins de 72 unités, voire complètement ruinés !
Pourquoi la richesse moyenne croît-elle alors que la plupart des individus deviennent de plus en plus pauvres ?
C’est le piège classique de la non-ergodicité. L’illusion qu’un autre essai peut tout inverser provient précisément du fait que nous confondons la moyenne collective avec le destin individuel.
Le piège de la non-ergodicité : la moyenne à long terme ≠ votre véritable destin
Qu’est-ce que l’ergodicité ?
Le concept d’ergodicité (Ergodicity) apparaît d’abord en physique statistique, puis exerce une influence profonde dans les domaines des probabilités, de la finance, des sciences comportementales et de l’apprentissage automatique. La question centrale qu’il aborde est : la moyenne à long terme s’applique-t-elle à l’individu ? Lorsque nous prenons des décisions, devrions-nous faire confiance à la « moyenne à long terme » ou plutôt à la réalité vécue par expérience directe ?
Au XIXe siècle, le physicien Ludwig Boltzmann proposa l’hypothèse d’ergodicité lors de ses recherches sur le mouvement des molécules de gaz : si l’on observe une molécule de gaz suffisamment longtemps, elle passera par tous les états possibles.
Imaginez un récipient fermé contenant d’innombrables molécules de gaz, chacune suivant des trajectoires de vitesse différentes au cours des collisions. La trajectoire à long terme d’une seule molécule est identique à la distribution statistique globale du gaz, ce qui signifie que l’on peut utiliser l’état de toutes les molécules à un instant donné pour inférer la trajectoire à long terme d’une molécule unique.
C’est ce que l’on appelle l’hypothèse ergodique de Boltzmann.

Mathématiquement, l’ergodicité implique que :
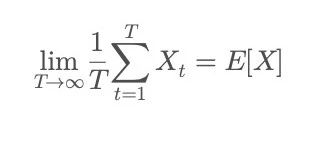
Le membre de gauche représente la moyenne temporelle : le résultat moyen obtenu par un individu après avoir subi suffisamment longtemps un même processus ;
Le membre de droite représente la moyenne d’ensemble : l’espérance statistique obtenue en observant simultanément un grand nombre d’individus à un instant donné. Autrement dit, lorsque le système est ergodique, le comportement d’un individu converge vers la « moyenne à long terme » du groupe.
Si le monde était ergodique, la richesse de chacun tendrait vers la richesse moyenne de la société. Dans un monde ergodique, tout le monde expérimenterait tous les états économiques possibles (richesse, pauvreté, succès, échec), et le destin individuel convergerait toujours vers la « moyenne à long terme » du groupe.
Mais la vie réelle est souvent non-ergodique : les ressources des individus sont limitées, et ils sortent souvent du jeu avant d’avoir pu explorer toutes les trajectoires possibles, suite à un échec fatal.
Nous entendons souvent des affirmations séduisantes telles que :
« Le revenu annuel moyen dans tel secteur dépasse le million. »
« Tel individu a atteint l’indépendance financière à 30 ans, après seulement deux ans d’entreprise. »
« Les fonds indiciels offrent un rendement annualisé élevé à long terme, il suffit d’investir régulièrement pour devenir riche. »
…
Ces statistiques apparemment raisonnables semblent nous révéler une vérité certaine. Comme si agir suffisait à garantir que le rendement moyen à long terme s’appliquerait à soi. Mais ces cas relèvent de processus non ergodiques, dépendants du chemin suivi et impossibles à reproduire. Les imitateurs ne peuvent pas revivre les mêmes contextes historiques, réseaux relationnels, coups de chance, ni même connaître le nombre caché des échecs silencieux.
Les données vous donnent la moyenne à long terme du groupe, mais la réalité regorge de « chutes brutales » à court terme.
C’est justement le piège le plus insidieux de la non-ergodicité — la moyenne statistique issue du big data ≠ le destin réel de l’individu.
Un seul effondrement peut être irréversible pour un individu ; un seul échec peut entraîner une sortie définitive du jeu, sans possibilité de retour à l’état « moyen ». Chaque trajectoire de vie n’est vécue qu’une fois ; nous ne pouvons pas, comme un casino, tirer profit de la moyenne à long terme du groupe en comptant sur la loi des grands nombres.
Pourquoi le destin à long terme de l’individu est-il généralement pire que la « moyenne » ?
Dans un système non ergodique, la performance individuelle à long terme est souvent inférieure à la moyenne du groupe. Ce n’est pas une coïncidence, mais une caractéristique structurelle systématique. Cette moyenne flatteuse est souvent tirée vers le haut par quelques histoires rares de réussite entrepreneuriale, enrichissement rapide ou retours spectaculaires, tandis que les échecs silencieux de la majorité restent invisibles dans les statistiques.
La plupart des systèmes réels sont de nature multiplicative et présentent une forte dépendance au chemin parcouru — comme les intérêts composés en investissement, le déclin de la santé ou la destruction de la réputation. Une caractéristique typique de ces systèmes est : la croissance est limitée, mais la chute peut être infinie.
Une seule faillite peut ruiner toute une vie ;
Une seule mauvaise décision peut changer irrémédiablement le destin ;
Un seul manquement peut détruire définitivement la confiance ;
Tandis que les gains possibles — richesse accumulée, performance améliorée, avantage acquis — sont toujours limités.
C’est pourquoi, mathématiquement, le taux de croissance à long terme d’un processus multiplicatif n’est pas égal au « rendement moyen », mais plutôt proche de :
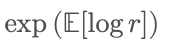
En comparaison, la moyenne du groupe utilise généralement la moyenne arithmétique :
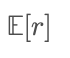
Et puisque la fonction logarithme est strictement concave, l’inégalité de Jensen implique que :
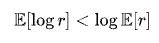
Ainsi, le taux de croissance à long terme d’un système multiplicatif (c’est-à-dire la moyenne géométrique) est toujours inférieur à la moyenne arithmétique. Plus la volatilité est élevée, plus cet écart est marqué. La moyenne arithmétique vous dit « ce qui se passerait si vous aviez toujours de la chance », tandis que la moyenne géométrique vous dit « combien il vous reste après avoir traversé les tempêtes du monde réel ».
Cela signifie que la performance individuelle à long terme est toujours bien inférieure au « rendement moyen du groupe », non pas par malchance, mais par structure.
Comment prendre la meilleure décision ? La ligne d’or de la formule de Kelly
Alors, dans la prise de décision au fil de la vie, que pouvons-nous faire pour éviter de finir ruinés dans un jeu à long terme ? Comment éviter la faillite tout en réalisant des gains composés durables ?
La réponse est : ne jamais tout miser, apprenez à parier selon Kelly !
Le critère de Kelly (Kelly Criterion) est une stratégie optimale de pari dans les jeux répétés, visant à maximiser les gains à long terme tout en évitant la ruine à court terme. Il a été initialement proposé en 1956 par John L. Kelly Jr. aux Bell Labs, dans le but d’optimiser la transmission d’information dans un canal bruité, en maximisant l’efficacité du transfert d’informations.
Cette théorie a rapidement franchi les frontières de son domaine d’origine.
Le mathématicien américain et génie de l’investissement Edward Thorp découvrit que la formule de Kelly permettait d’optimiser la trajectoire de croissance de la richesse. Il l’appliqua d’abord au casino, battant systématiquement le croupier au blackjack dans son livre Beat the Dealer, puis à Wall Street, continuant à « récolter » dans Beat the Market.
Ce principe équivaut fondamentalement à maximiser l’espérance logarithmique du gain (log-utility), assurant ainsi un équilibre dynamique entre croissance et risque. Il vous aide à trouver le point optimal entre « rester en vie » et « gagner suffisamment ».
Formule de Kelly :
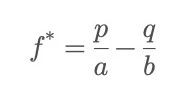
Où p est la probabilité de succès, q = 1-p celle d’échec ; b est le ratio de gain (hors mise), et a est la proportion perdue en cas d’échec (souvent 1, si toute la mise est perdue).
Revenons au jeu de pile ou face présenté en introduction : vous pouvez choisir de miser une fraction fixe de votre capital à chaque tour. Mais quelle fraction est optimale ?
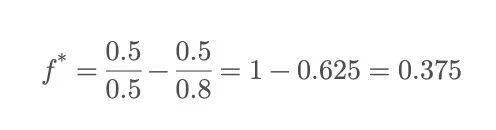
Autrement dit, la formule de Kelly recommande de miser 37,5 % de votre capital total à chaque tour. Miser trop expose à la ruine rapide même avec un avantage ; miser trop peu fait manquer des opportunités de croissance.
L’intérêt de la formule de Kelly réside dans le fait de trouver ce point où l’on gagne le plus possible tout en survivant.
Précisons que la formule de Kelly est très sensible aux estimations de probabilité et de cote, or ces paramètres sont souvent incertains ou variables en pratique. C’est pourquoi de nombreux praticiens prudents utilisent la moitié de la valeur suggérée par Kelly (stratégie dite « demi-Kelly »), afin d’obtenir une trajectoire de gains plus lisse.
Simulation : 100 000 joueurs à pile ou face, combien « survivent » ?
Pour mieux comprendre l’impact des différentes stratégies de pari sur le destin individuel, j’ai simulé un jeu de pile ou face impliquant 100 000 joueurs, sur 200 tours, chaque joueur jouant indépendamment.
Les règles restent les mêmes : capital initial de 1000, gain de 80 % en cas de face, perte de 50 % en cas de pile. Les joueurs choisissent un pourcentage fixe de mise : 100 %, 65 %, 37,5 %, etc.
Le résultat ? Les joueurs misant 100 % ont presque tous disparu !
La richesse finale suit une « distribution en loi de puissance » : bien qu’une minorité devienne extrêmement riche, la majorité des joueurs finissent ruinés.
Nous comparons ici la distribution de richesse sous quatre stratégies de mise différentes, la richesse étant représentée vers la droite.
a. Mise à 100 % : presque tout le monde en faillite
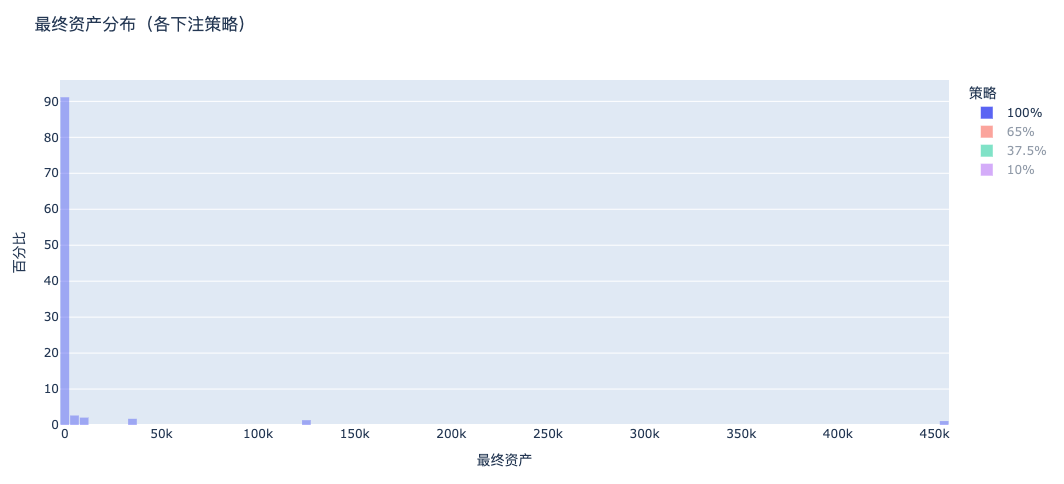
La distribution des actifs finaux avec mise totale présente un énorme pic à gauche (pauvreté) et une queue très fine à droite (richesse extrême) : la majorité fait faillite, une poignée emporte tout. C’est la manifestation concrète d’une asymétrie du jeu + du biais de survivant.
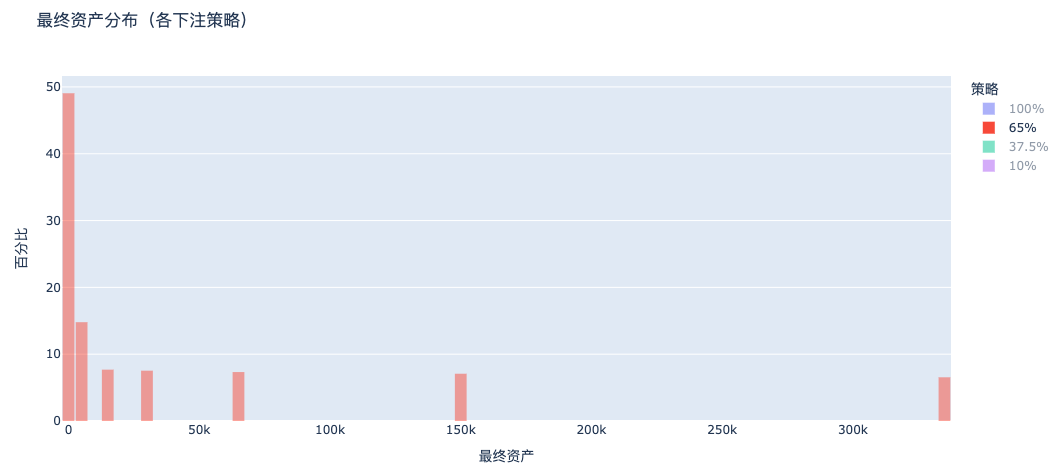
b. Mise à 65 % : toujours fortement polarisée, beaucoup font encore faillite
c. Mise à 37,5 % (formule de Kelly) : croissance stable de la richesse
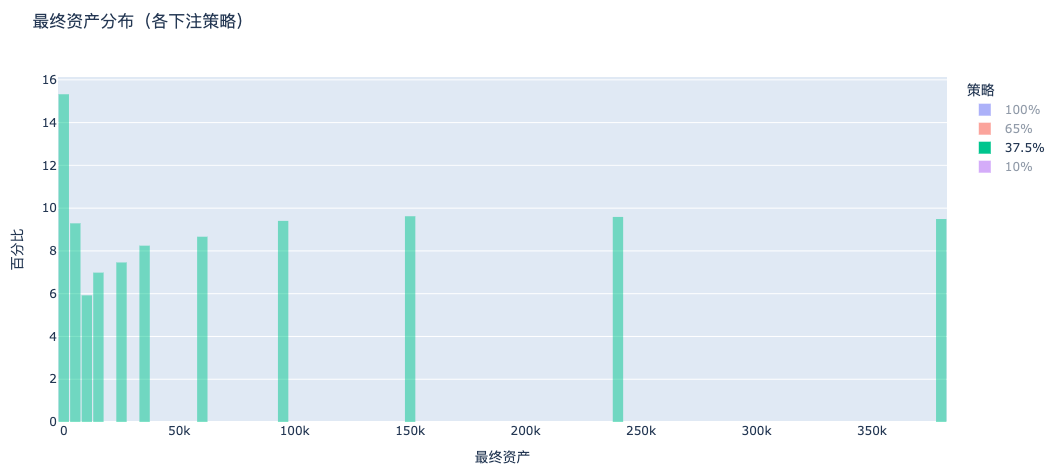
Sous la stratégie de Kelly, la distribution des actifs se décale nettement vers la droite, la majorité voit sa richesse augmenter, avec une concentration notable — c’est le modèle optimal d’accumulation de richesse.
d. Mise à 10 % : presque personne ne fait faillite, mais rendement trop faible
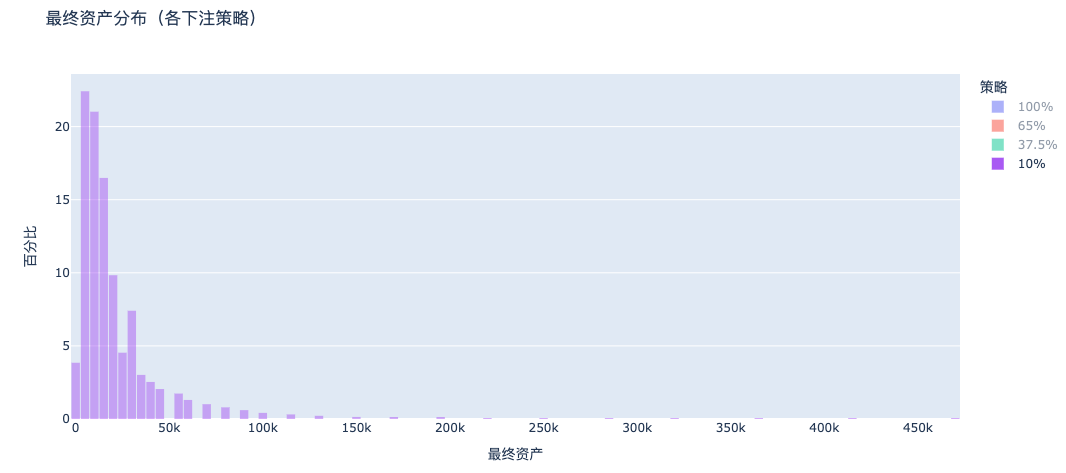
On n’observe plus de pic de faillite comme avec la mise totale, mais la richesse reste concentrée dans la zone basse. En comparaison, la stratégie à 37,5 % développe une longue traîne à droite, permettant une multiplication significative des actifs.
La stratégie de Kelly est la seule à concilier « ne pas faire faillite dans la majorité des cas » et « croissance substantielle ». Elle constitue mathématiquement la meilleure stratégie de survie à long terme. Telle est l’essence de la formule de Kelly : elle ne cherche pas à vous faire gagner le plus, mais à vous assurer de survivre assez longtemps.
La philosophie de vie dans la formule de Kelly
La formule de Kelly nous enseigne que le secret du succès à long terme réside dans le contrôle de la taille de ses « paris ». La vie ne consiste pas à porter un coup critique, mais à savoir rester en jeu.
Dans sa carrière, il ne s’agit ni de démissionner impulsivement, ni de rester figé dans sa zone de confort, mais de construire progressivement, renforcer ses compétences, oser changer de voie, tout en gardant une option de secours ;
Dans l’investissement, il ne s’agit pas de tout miser pour s’enrichir vite, mais de contrôler la taille de ses positions selon les cotes, et conserver ses jetons ;
Dans les relations, il ne s’agit pas de placer toute son émotion et sa valeur sur une seule personne, mais d’investir tout en préservant son autonomie ;
Dans la croissance personnelle et l’autodiscipline, il ne s’agit pas de compter sur un seul élan pour tout transformer, mais d’optimiser durablement sa structure de vie grâce à des gains composés.
La vie est comme un jeu très long : votre objectif n’est pas de gagner une fois, mais de vous assurer de pouvoir continuer à jouer. Tant que vous ne sortez pas du jeu, quelque chose de bon finira par arriver.
Bienvenue dans la communauté officielle TechFlow
Groupe Telegram :https://t.me/TechFlowDaily
Compte Twitter officiel :https://x.com/TechFlowPost
Compte Twitter anglais :https://x.com/BlockFlow_News