
BiB Exchange : le miracle de la liquidité financière, révélation de la logique de couverture, maîtrise des risques d'imbalance
TechFlow SélectionTechFlow Sélection

BiB Exchange : le miracle de la liquidité financière, révélation de la logique de couverture, maîtrise des risques d'imbalance
Cet article explorera en profondeur le cœur de la liquidité et analysera comment des instruments tels que les options et les contrats perpétuels peuvent devenir des outils efficaces pour atténuer les risques d'illiquidity.
Rédaction : BiB Exchange
Introduction
Dans l’univers de la cryptographie, des plateformes telles qu’Uniswap et Curve brillent indéniablement comme des étoiles financières. Toutefois, face au risque d'impact impermanent (impermanent loss), les investisseurs doivent aujourd'hui relever un défi crucial : comment réaliser intelligemment une couverture efficace ? Dans cette exploration approfondie de la logique de couverture, BiB Exchange plonge au cœur de la liquidité pour analyser comment des outils tels que les options et les contrats perpétuels peuvent devenir des alliés précieux dans la gestion du risque d’impact impermanent.
Les fournisseurs de liquidité (LP – Liquidity Providers) constituent l'un des modèles économiques les plus courants dans le secteur DeFi. Leur rôle principal consiste à alimenter des pools de liquidité afin de générer des rendements via le minage de liquidité, obtenir des prêts en cryptomonnaies ou transférer les droits sur une liquidité mise en gage. Ce modèle repose essentiellement sur un système de marché automatisé (AMM – Automated Market Maker), où les LP déposent deux ou plusieurs jetons dans un pool pour fournir de la liquidité, et perçoivent en retour une part des frais de transaction. Cependant, cette méthode expose souvent à un risque d’impact impermanent.

Cet article de BiB Exchange se concentre sur trois parties principales : la première présente les mécanismes AMM courants sur le marché et leurs caractéristiques ; la deuxième explique l’impact impermanent et ses propriétés fonctionnelles à travers le cas d’Uni V2 ; la troisième examine plusieurs méthodes fréquentes de couverture contre l’impact impermanent — notamment la couverture dynamique, les contrats perpétuels puissants (perpetual power contracts) et les options — tout en comparant leurs avantages et inconvénients respectifs.
I. Introduction aux AMM
En déposant des fonds dans un pool de liquidité, les utilisateurs deviennent des fournisseurs de liquidité (Liquidity Providers). Le principe sous-jacent à ces pools repose sur le mécanisme du Marché Automatisé (Automated Market Maker, AMM), plus précisément appelé Marché à Fonction Constante (Constant Function Market Makers, CFMMs). Ce système s’exécute sur des plateformes décentralisées sans intermédiaire traditionnel, prend en charge des paires multi-actifs, et présente plusieurs caractéristiques marquantes :
-
Absence de carnet d'ordres : Contrairement aux bourses centralisées traditionnelles, les AMM ne reposent pas sur un carnet d’ordres d’achat et de vente. Les transactions sont exécutées directement via des contrats intelligents, sans besoin de correspondance entre acheteurs et vendeurs.
-
Frais de transaction : Chaque opération génère des frais reversés aux fournisseurs de liquidité, proportionnels à leur part dans le pool. Ce modèle incite à fournir davantage de liquidité, stimulant ainsi l’activité du marché.
-
Ajustement continu des prix : Grâce aux algorithmes AMM, les prix des actifs s’ajustent continuellement selon l’offre et la demande. Cela permet d’obtenir instantanément la quantité d’actif souhaitée, sans attendre la correspondance d’un ordre.
Les principaux protocoles DEX utilisent actuellement plusieurs types d’algorithmes AMM :
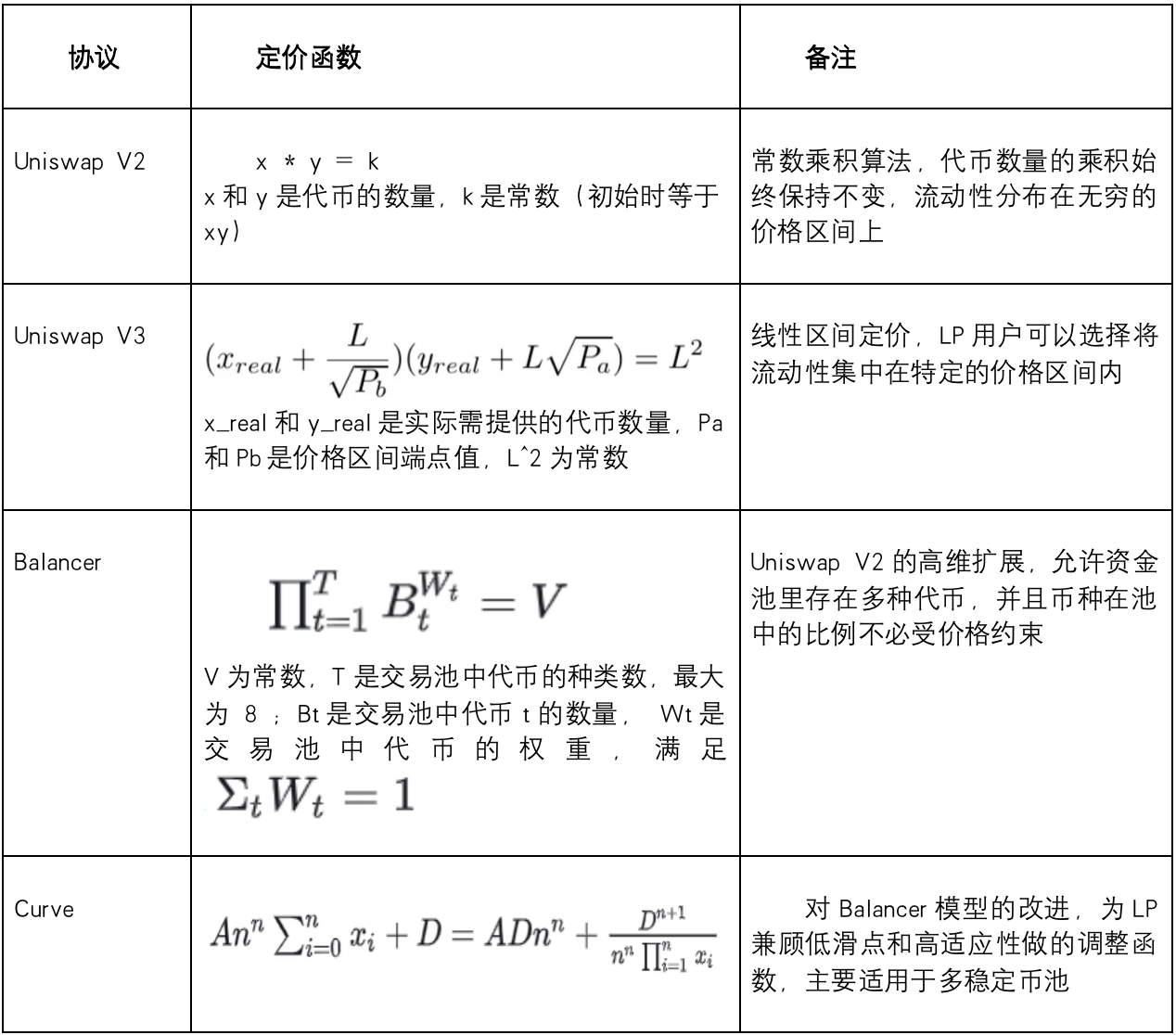
Sur ces protocoles, les traders paient des frais proportionnels à chaque transaction, dont une partie est redistribuée aux fournisseurs de liquidité. Toutefois, en raison du risque d’impact impermanent, les LP doivent constamment évaluer le rapport entre les revenus générés par les frais et les pertes potentielles.

Pendant la période où les fournisseurs de liquidité détiennent leurs actifs dans le pool, toute fluctuation du prix des cryptomonnaies crée un écart entre le prix du marché et celui du pool, ouvrant ainsi une opportunité d’arbitrage. Les arbitragistes effectuent alors des opérations jusqu’à ce que les proportions des actifs dans le pool reflètent fidèlement les prix du marché. Pendant ce processus, les fournisseurs de liquidité perçoivent des frais issus des transactions des arbitragistes, tandis que ces derniers réalisent un profit sur l’écart de prix, ce qui entraîne une perte potentielle pour les LP : l’impact impermanent.
II. Propriétés fonctionnelles
À travers le mécanisme AMM d’Uniswap V2, BiB Exchange explique ici comment survient l’impact impermanent. Ce dernier utilise l’équation X*Y=K pour calculer les prix des deux monnaies dans le pool, où X et Y représentent les quantités respectives des deux actifs, et K une constante.
Supposons que les deux actifs X et Y dans le pool soient ETH et DAI, et qu’un utilisateur y dépose 1 ETH et 100 DAI. Selon le mécanisme AMM, les paires de jetons déposées doivent avoir une valeur égale. Ainsi, au moment du dépôt, 1 ETH = 100 DAI. La valeur totale du dépôt est donc de 200 dollars. Si le pool contient au total 10 ETH et 1 000 DAI, sa liquidité totale est de 2 000 dollars. L’utilisateur détient alors 10 % du pool, avec une constante K = 10 × 1 000 = 10 000.
Imaginons maintenant que le prix spot de l’ETH sur BiB Exchange monte à 400 DAI, tandis que le prix dans le pool reste à 100 DAI. Un arbitragiste repère alors une opportunité et injecte des DAI dans le pool tout en retirant des ETH, jusqu’à ce que la proportion des actifs reflète le prix du marché. Selon le principe du produit constant (K = 10 000), le pool contiendra désormais 5 ETH et 2 000 DAI (en négligeant les frais).
Si l’utilisateur décide alors de retirer ses fonds, il récupère 10 % du pool, soit 0,5 ETH et 200 DAI, pour une valeur totale de 400 dollars. Bien qu’il soit bénéficiaire, s’il avait simplement conservé ses actifs (1 ETH + 100 DAI), il aurait obtenu 500 dollars ! En agissant comme fournisseur de liquidité, il subit donc une perte de 100 dollars. Cette somme représente son impact impermanent.
Note : Ce scénario ignore les frais perçus par le fournisseur de liquidité.
Procédons maintenant à une brève démonstration mathématique :
Soit P le prix de l’ETH exprimé en DAI stablecoin, donc P = Y/X
En combinant les deux équations X*Y=K et P=Y/X, on obtient :
X = (K/P)^0.5 ; Y = (K*P)^0.5
Considérons deux instants T0 et T1, avec des prix respectifs P0 et P1, où P1=*P0 (représente le facteur de variation du prix)
La valeur du pool à T1 est : 2*Y1 = 2*(K**P0)^0.5
Sans être LP, la valeur initiale des actifs à T1 serait : X0*P1+Y0 = (1+)*(K*P0)^0.5
Impact impermanent = [X1*Y1 - (X0*P1+Y0)] / (X0*P1+Y0) = 2^0.5/(1+) - 1
= -(^0.5 - 1)^2 / (1+) <= 0 (toujours vrai)
On observe donc que toute variation de prix entraîne nécessairement un impact impermanent pour le LP.
Le graphique ci-dessous illustre la fonction d’impact impermanent selon différentes amplitudes de variation de prix :
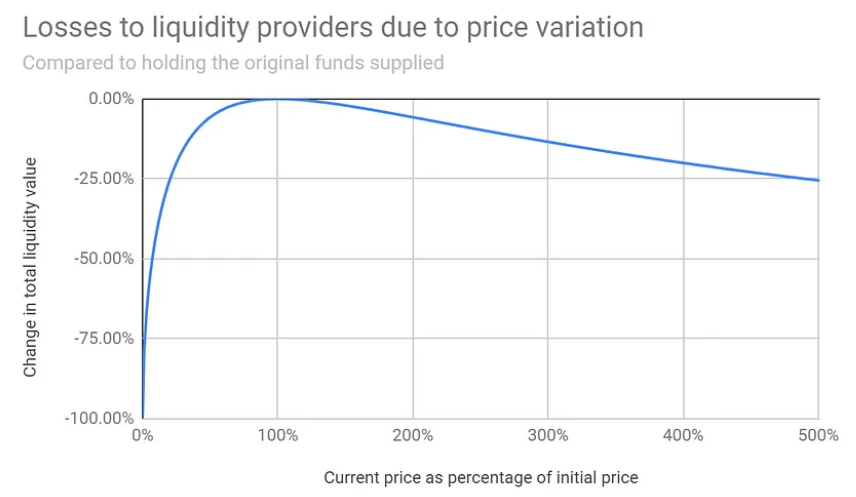
Le graphique montre clairement que plus la volatilité du prix est élevée, plus l’impact impermanent augmente. Toutefois, si ce dernier reste inférieur aux frais générés, l’utilisateur peut toujours réaliser un profit.
Pour les autres mécanismes AMM courants, la fonction d’impact impermanent suit un comportement similaire : toute fluctuation de prix expose les LP à un impact impermanent. Comment alors éviter cette perte ? Examinons quelques stratégies possibles.
III. Couverture contre l’impact impermanent
Reprenons l'exemple précédent : les deux actifs X et Y dans le pool sont ETH et DAI, avec un dépôt initial de 1 ETH et 100 DAI, dont les valeurs sont équivalentes (prix de l’ETH, P = 100/1 = 100).
Nous prenons comme référence un portefeuille composé à 50 % d’un actif volatile et à 50 % d’une monnaie stable (bien que d'autres références soient possibles, comme détenir uniquement l’actif volatile). Analysons ensemble comment éviter l’impact impermanent.
La valeur du portefeuille de détention 50 % est V_HODL_50() = (1+)*(K*P0)^0.5, une fonction linéaire par rapport à (variation du prix).
Tandis que la valeur du LP, V_LP() = 2*(K**P0)^0.5, suit une racine carrée, donc non linéaire. Cette non-linéarité existe dans tous les mécanismes AMM raisonnables (avec des formes fonctionnelles variées).
Introduisons deux concepts clés :
-
Delta : dérivée première de la valeur du portefeuille par rapport au prix, mesurant la sensibilité du portefeuille à une variation de prix.
-
Gamma : dérivée seconde, ou taux de variation du delta par rapport au prix.
On observe que le gamma du portefeuille de référence est toujours nul, tandis que celui du LP est systématiquement négatif.
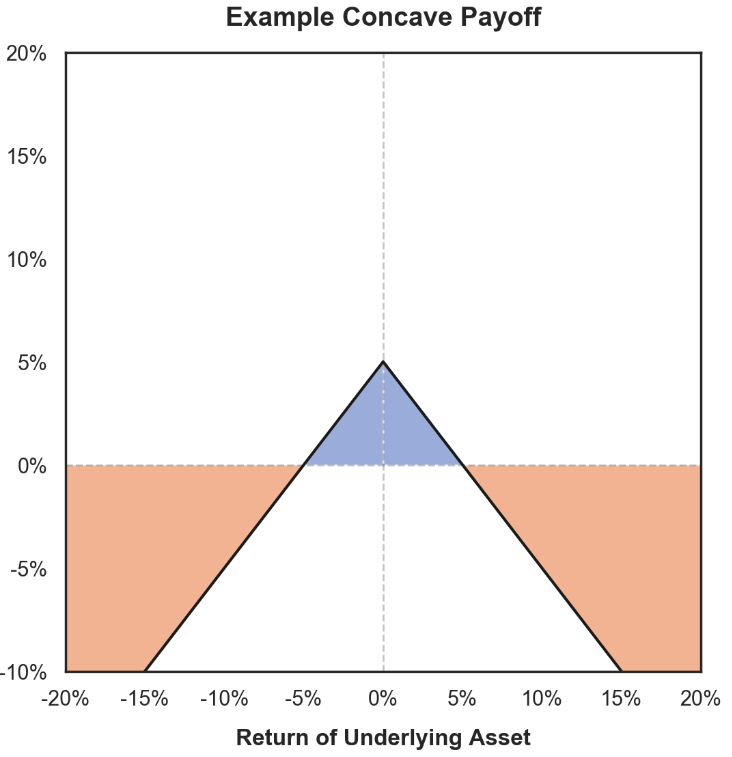
Revenu à gamma négatif : profits réduits à la hausse, pertes amplifiées à la baisse
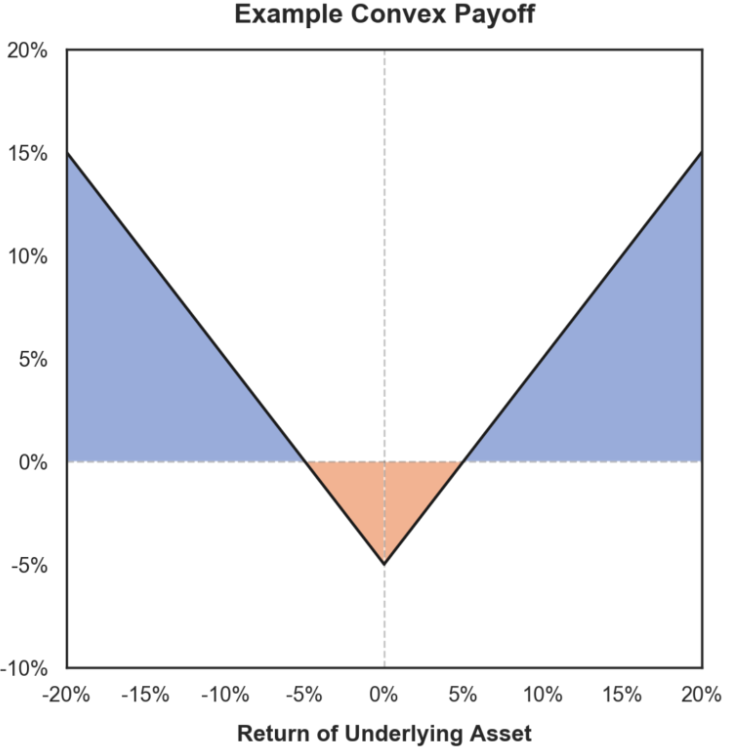
Revenu à gamma positif
Face à ce gamma négatif, quelles solutions BiB Exchange propose-t-il ?
1) Maximiser les revenus de frais : tant que les frais dépassent l’impact impermanent, le LP reste rentable ;
2) Choisir des paires à faible volatilité ;
3) Réajuster dynamiquement la position lors des variations de prix ;
4) Utiliser des instruments financiers à gamma positif (comme les options ou les contrats perpétuels puissants) pour couvrir la position.
3.1 Contrats perpétuels
Maximisation des revenus de frais : cela revient essentiellement à choisir judicieusement le pool et le niveau de frais, et à anticiper l’évolution du marché — une démarche plus proche du trading que de l’investissement passif. Il convient non seulement d’examiner le taux de rendement annuel (APY) du pool, mais aussi d’utiliser des indicateurs tels que la volatilité implicite (IV — Implied Volatility, déduite du prix des options) ou le ratio de Sharpe (mesurant le rendement excédentaire par unité de risque).
Choix de paires à faible volatilité : les paires stables subissent rarement un impact impermanent, mais présentent un risque (faible) de décrochage pouvant entraîner des pertes catastrophiques.
Couverture dynamique : examinons une stratégie native DeFi basée sur l’emprunt. Comparée à la couverture via contrat perpétuel, elle nécessite plus de capital initial, mais est relativement sûre et facile à mettre en œuvre.
Alice commence avec 5 000 USDC et fournit de la liquidité dans un pool USDC/ETH. Le prix initial de l’ETH est de 1 000 USDC.
Elle place 4 000 USDC sur Aave, emprunte 1 ETH, puis constitue une position Uniswap complète (fourchette totale) à hauteur de 50/50.
Son capital initial de 5 000 USDC est divisé en garantie (valeur 3 000 USDC) et pool (valeur 2 000 USDC) :
V_collateral = 4 000
V_debt = 1 000 ; V_hedge = 4 000–1 000 = 3 000
V_capital = V_pool + V_hedge = 5 000
Le prix de l’ETH double, atteignant 2 000 USDC. La valeur du pool passe à 2 000·sqrt(2) USDC, mais celle de la couverture chute à 2 000 USDC :
V_collateral = 4 000 ; V_debt = 2 000 ; V_hedge = 4 000–2 000 = 2 000
V_capital = V_pool + V_hedge = 2 000 (1 + sqrt(2)) = 4 828 USDC
Une perte de 3,4 % par rapport au capital initial. Hormis le coût d’opportunité, aucun coût de couverture n’est engendré, car les frais d’emprunt sont généralement inférieurs au taux d’intérêt du prêt.
Bob adopte la même stratégie initiale. Mais quand le prix de l’ETH atteint 1 500 $, Bob remarque que le pool contient moins de 1 ETH, et rembourse donc partiellement son emprunt tout en restant parfaitement couvert. Il retire des USDC d’Aave, les échange contre de l’ETH, et rembourse exactement la quantité d’ETH empruntée. Quand le prix atteint 2 000 $, Bob subit encore une perte, mais moindre qu’Alice.
Explication intuitive : pour rembourser, Alice doit acheter de l’ETH à 2 000 $, tandis que Bob l’a acheté à 1 500 $.
Mais si le prix redescend de 1 500 à 1 000 $, Bob supporte des coûts de transaction et de swap, contrairement à Alice. En outre, après cette baisse, Bob doit rééquilibrer dans l’autre sens : emprunter plus d’ETH, le vendre contre des USDC, et déposer ceux-ci comme garantie sur Aave.
Exprimons cela mathématiquement. Nous connaissons déjà la formule de l’impact impermanent :
DL() = -(^0.5 - 1)^2 / (1+) <= 0
Et : V_HODL_50() = (1+)*(K*P0)^0.5 ; V_LP() = 2*(K**P0)^0.5
On peut décomposer la valeur du LP comme suit :
V_LP() = V_HODL_50() + V_HODL_50() * DL()
Objectif : couverture delta neutre. Construire un portefeuille de couverture ayant un rendement inverse à celui du portefeuille HODL 50/50 :
V_hedge(_H) := V0 - V_HODL_50(_H)
Ici, _H désigne le ratio de prix utilisé pour construire la couverture. Si = _H, la position est véritablement delta neutre : de petites variations du prix n’affectent pas significativement la valeur du portefeuille.
V_portfolio() =
= V_HODL_50() + V_HODL_50()*DL() + V_hedge() - hedging_costs
= V0 + V_HODL_50()*DL() — hedging_costs
Remarques :
a. Fonction non linéaire : le terme V_HODL_50()*DL() (toujours ≤ 0) représente la perte due aux variations de prix. Il est nul lorsque =1. En limitant les variations de prix, ce terme reste proche de zéro car il est non linéaire.
b. Hedging_costs : inclut les frais de transaction et l’impact de prix lors de l’achat/vente des actifs de couverture.
L'idée est de rééquilibrer la couverture chaque fois que dépasse un seuil fixe, appelé « pas de rééquilibrage ».
Pour limiter les pertes à chaque étape, les LP rééquilibrent leur couverture dès que le prix varie au-delà du seuil. Le coût de couverture augmente quand le pas diminue, mais le terme d’impact impermanent peut être rendu arbitrairement petit. Huobi utilise ce mécanisme dans son minage sans perte mono-actif.
c. Choix de la fréquence de rééquilibrage dynamique : l’équation de valeur du portefeuille suffit pour évaluer l’effet du pas de rééquilibrage sur la performance.
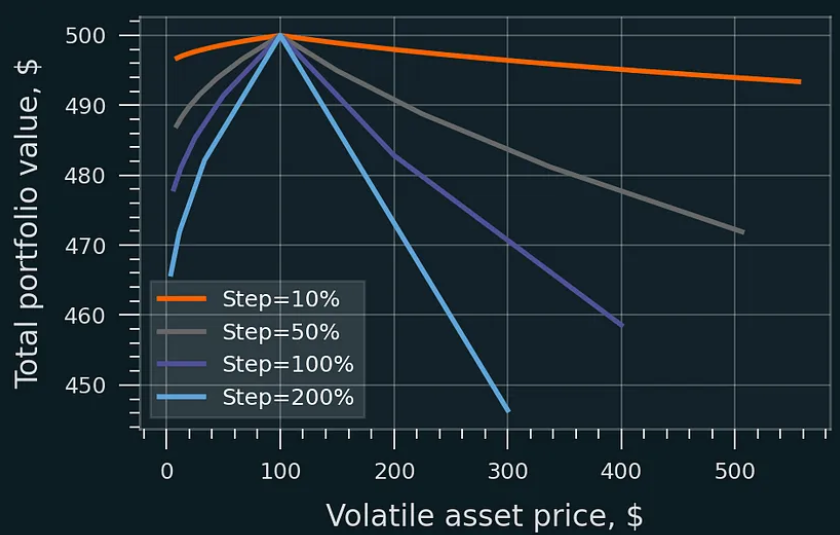
Des pas plus petits réduisent les pertes. Les coûts de rééquilibrage et les frais LP ne sont pas inclus. Prix initial : 100 $, valeur initiale de la position LP : 200 $.
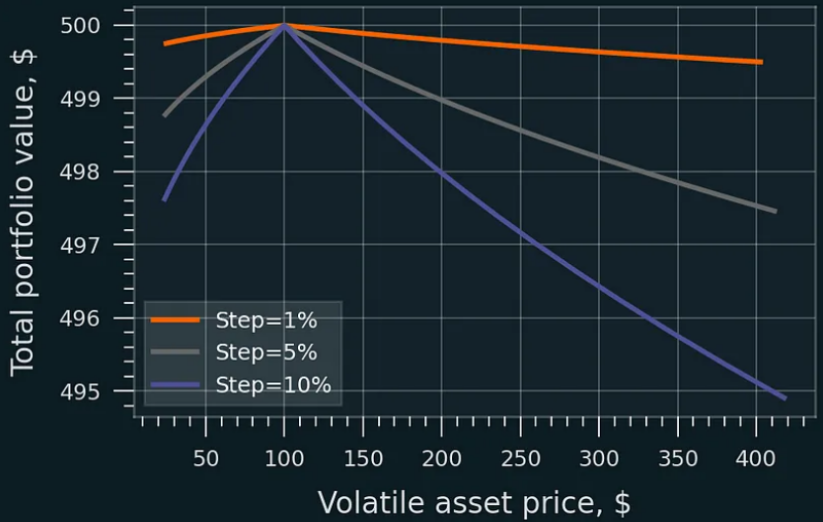
Avec des pas très petits, l’impact impermanent disparaît. Coûts et frais exclus. Même configuration initiale.
Le graphique suivant montre les coûts de couverture estimés via simulation GBM (marche aléatoire), avec un frais de swap de 0,3 %, sans frais de transaction. Sur Uniswap V2 (fourchette totale), même de petits pas (1 à 2 %) restent peu coûteux :
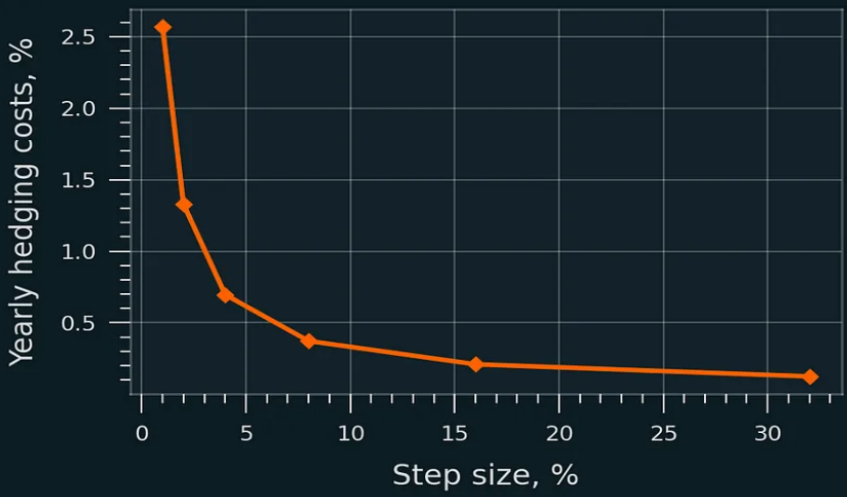
Coût annuel de swap de la couverture en % du capital initial ; Uniswap v2. En concentration de liquidité, les coûts sont plus élevés mais restent faibles relativement au capital.
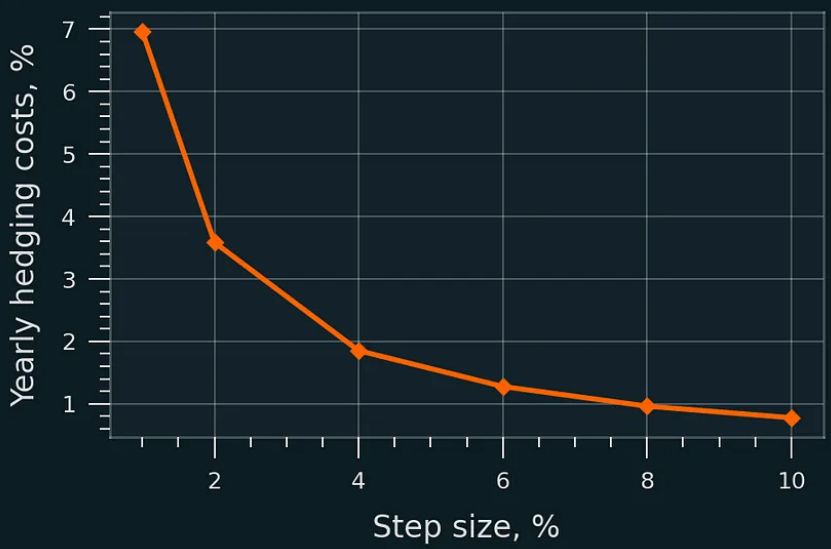
Coût annuel de swap de la couverture en % du capital initial ; Uniswap v3 ; plage de prix : [P/1.5, P*1.5], sans migration de liquidité.
Jusqu’ici, nous avons discuté de stratégies delta neutres sur fourchette totale. Mais elles s’appliquent aussi à d’autres cas. Par exemple, si seul 50 % de l’actif volatile peut être emprunté, on obtient une stratégie mixte : moitié fonction sqrt(), moitié delta neutre.
De plus, le montant emprunté pourrait dépendre du prix. Supposons qu’à prix initial, le LP emprunte 100 % de l’actif volatile, puis réduise progressivement cet emprunt à zéro en cas de hausse. À la baisse, il ferait l’inverse : emprunter plus de 100 %, vendre contre stablecoin. Cela forme une fonction convexe :

Comparaison entre détention, couverture partielle et dynamique. Pas = 1 %. Frais non affichés.
Note importante : pour les positions Uniswap v3 à plage fixe, le rééquilibrage de la couverture doit s’accompagner d’un repositionnement de la liquidité dans le pool.

Points clés :
a. En couvrant et en rééquilibrant régulièrement, les LP peuvent protéger leur capital contre les variations de prix. Une stratégie delta neutre est réalisable.
b. En utilisant un seuil de variation de x% pour déclencher le rééquilibrage, l’impact impermanent peut être minimisé.
c. Plus le pas de prix est petit, plus le résidu d’impact impermanent diminue. Mais un pas plus petit augmente les coûts de couverture.
3.2 Contrats perpétuels puissants (Power Perpetuals)
Achat d’instruments financiers à gamma positif : BiB Exchange présente ici deux outils — les contrats perpétuels puissants (power perpetuals) et les options. Commençons par les premiers.
Contrats perpétuels puissants : concept nouveau, basé sur la fonction puissance du prix d’un actif (carré, cube, etc.). Si le prix de l’ETH double, le prix du perpétuel ETH² quadruple, ETH³ octuple, ETH⁵ multiplie par 32.
Le graphique ci-dessous compare les rendements des contrats perpétuels puissants et des contrats perpétuels à effet de levier :
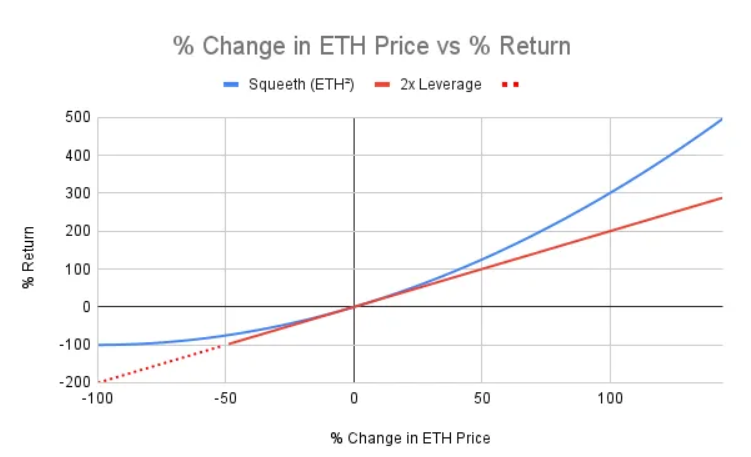
Le perpétuel ETH² (Squeeth) offre un rendement supérieur à un levier 2x à la hausse, et des pertes moindres à la baisse.
Exemple concret :
Alice souhaite couvrir sa position de liquidité USDC/WETH à fourchette complète. Elle consulte le tableau paramétrique suivant :
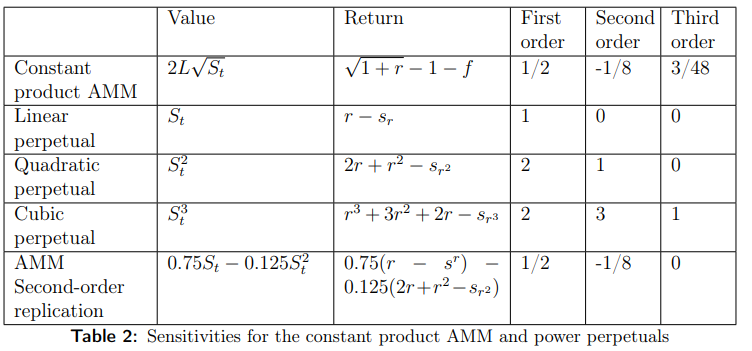
Explication du tableau :
-
Value : fonction de valeur du portefeuille selon différents modèles ;
-
Return : rendement, où r ≈ 0 est une petite variation de prix, « Sr, Sr², Sr³ » sont les taux de financement des perpétuels d’ordre 1, 2, 3 ; le calcul utilise un développement de Taylor ;
-
First, Second, Third order : coefficients du développement de Taylor du rendement.
Alice constate qu’elle doit prendre une position courte de 50 % sur l’ETH et longue de 12,5 % sur ETH² (pourcentages calculés à partir de V(LP), la valeur totale du capital bloqué). Elle vend short l’ETH normalement (via contrat perpétuel ou emprunt), puis se rend sur Opyn ou autre protocole de power perps pour acheter la quantité requise de Squeeth. Ce dernier est un dérivé dont le prix évolue comme le carré du prix de l’ETH.
Si des perpétuels d’ordre supérieur étaient disponibles, elle pourrait aussi prendre une longue position de 3/48 * V(LP) sur ETH³ et une courte de 15/384 * V(LP) sur ETH⁴, etc.
Si Alice veut imiter un portefeuille HODL 50/50, elle n’ouvre pas de position courte sur l’ETH, mais achète directement des perpétuels puissants d’ordre 2 ou plus (voir graphique).
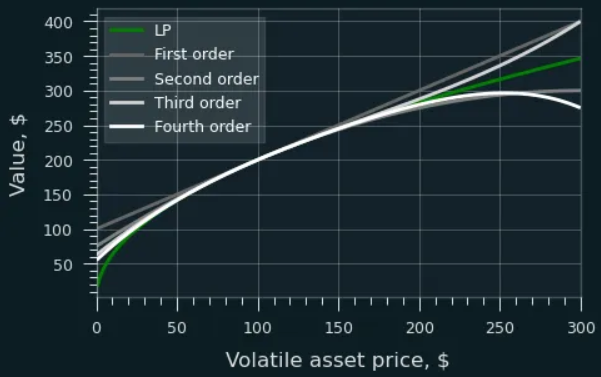
La fonction de valeur du LP peut être approximée par une série de perpétuels puissants. Plus l’ordre est élevé, meilleure est l’approximation.
Le graphique montre comment le rendement du LP est ajusté par une série de perpétuels puissants. Ces derniers nécessitent un rééquilibrage occasionnel, mais contrairement aux couvertures linéaires (rééquilibrage tous les 1-5 %), ils offrent une précision suffisante même sur des variations de 50-100 %.
Toutefois, très peu de protocoles proposent ces instruments. Seul Squeeth d’Opyn s’est imposé, et même lui manque de liquidité. BiB Exchange juge cette méthode peu pratique pour l’instant.
3.3 Options
1. Définir votre position stratégique :
Supposons un prix initial de l’ETH à 1 000 $. Partons de 1 000 USDC (ligne de base). Vendons-en 50 % en ETH :
x0 = 0,5 ETH
y0 = 500 USDC
Nous fournissons 0,5 ETH et 500 USDC dans un pool ETH-USDC.
2. Calculer la courbe de rendement de la position.
Valeur LP Uni V2 : V = 2*L*S^0.5 + frais
S = prix spot de l’ETH
L = (x0 * y0)^0.5
Moins le capital initial :
Rendement = 2*L*S^0.5 + frais - 1 000
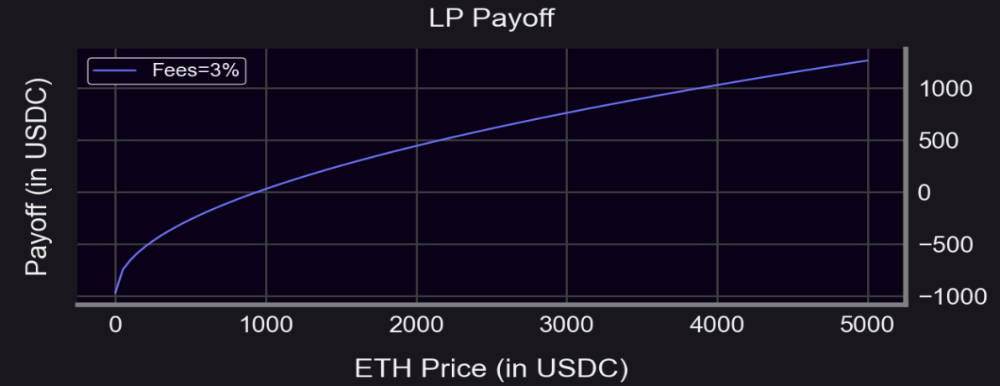
Pour Uni V3, c’est plus complexe :
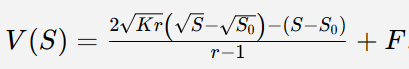
Où :
F = frais cumulés ;
K = (borne sup × borne inf)^0.5 ;
S0 = prix initial ;
r = (borne sup / borne inf)^0.5.
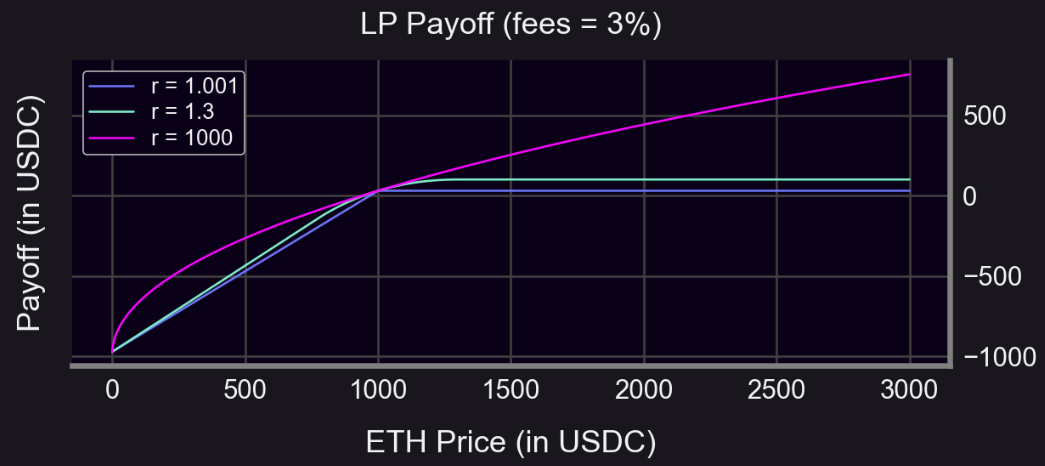
On observe que plus r est grand, plus la courbe de rendement LP se rapproche de celle de Uni V2. En outre, à l’extérieur de la plage, la structure ressemble à celle d’une option. On peut donc utiliser les méthodes suivantes :
Prix initial de l’ETH = 1 000
Acheter 1 option put ATM (prix d’exercice = 1 000 $)
Prime du put = 50
Frais LP = 3 % (r = 1,3, plage : prix_initial/1,3 à prix_initial*1,3)
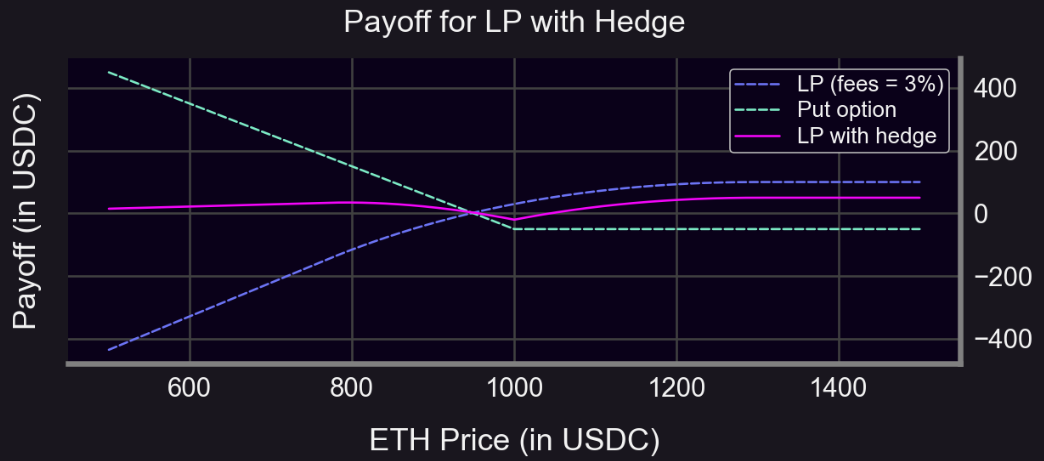
Quand S < 1 000 : rendement de couverture plus plat (parfois positif)
Quand S ≥ 1 000 : rendement de couverture plus faible (en raison de la prime)
La couverture coûte toujours des dollars. Il faut générer assez de frais pour couvrir ce coût.
Si on prend comme référence un portefeuille 50/50 ETH-USDC, on peut utiliser un straddle :
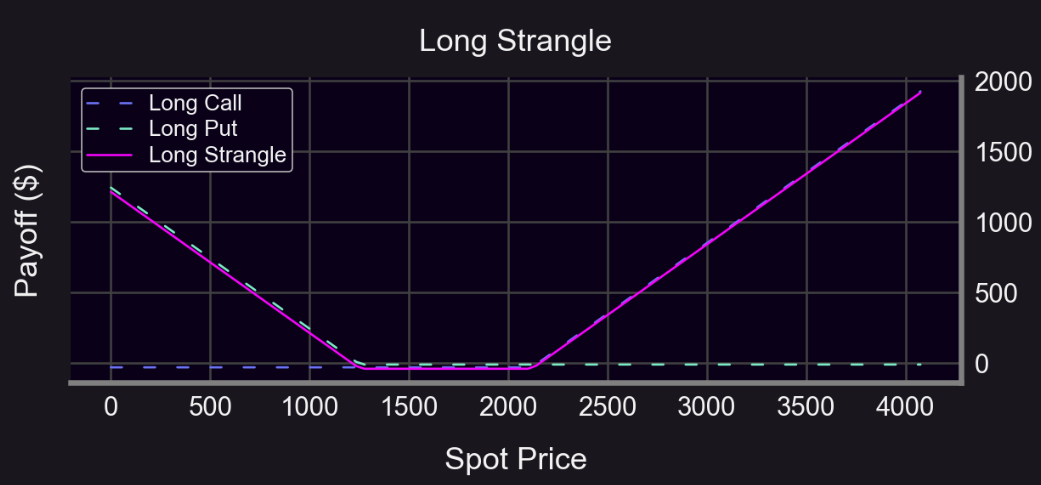
On constate aisément qu’avec un straddle, même en cas de forte volatilité (hausse ou baisse prononcée), l’impact impermanent reste limité :
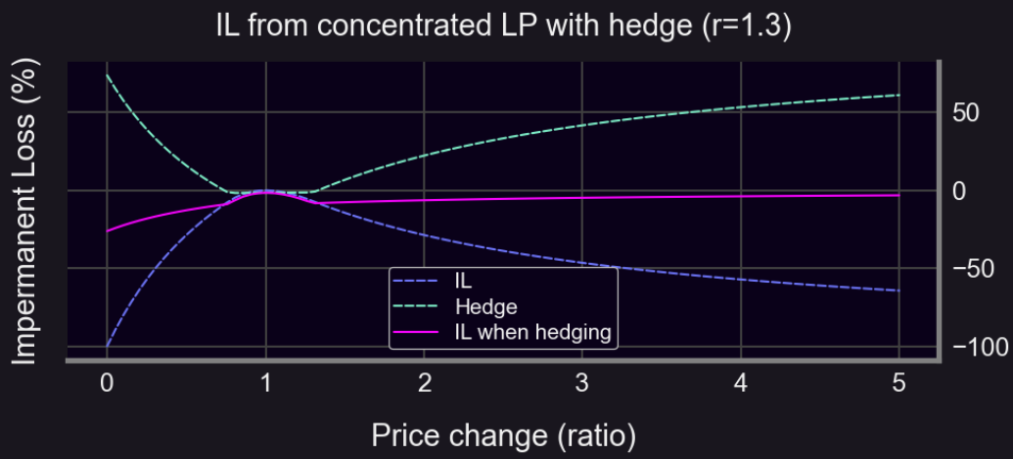
Panoptic propose des options perpétuelles pour la couverture. Les détenteurs peuvent choisir d’opérer une couverture pour réduire leur risque. Les fournisseurs de liquidité peuvent participer en fournissant la liquidité nécessaire et percevoir des frais. Ces options perpétuelles ouvrent une nouvelle voie pour couvrir Uniswap. BiB Exchange considère que couvrir le gamma permet une gestion plus complète du risque, tout en bénéficiant de la liquidité des power perps.
Résumons brièvement les avantages et inconvénients de chaque outil. Il s’agit d’une comparaison générale, les résultats réels pouvant varier selon les conditions spécifiques et le marché.
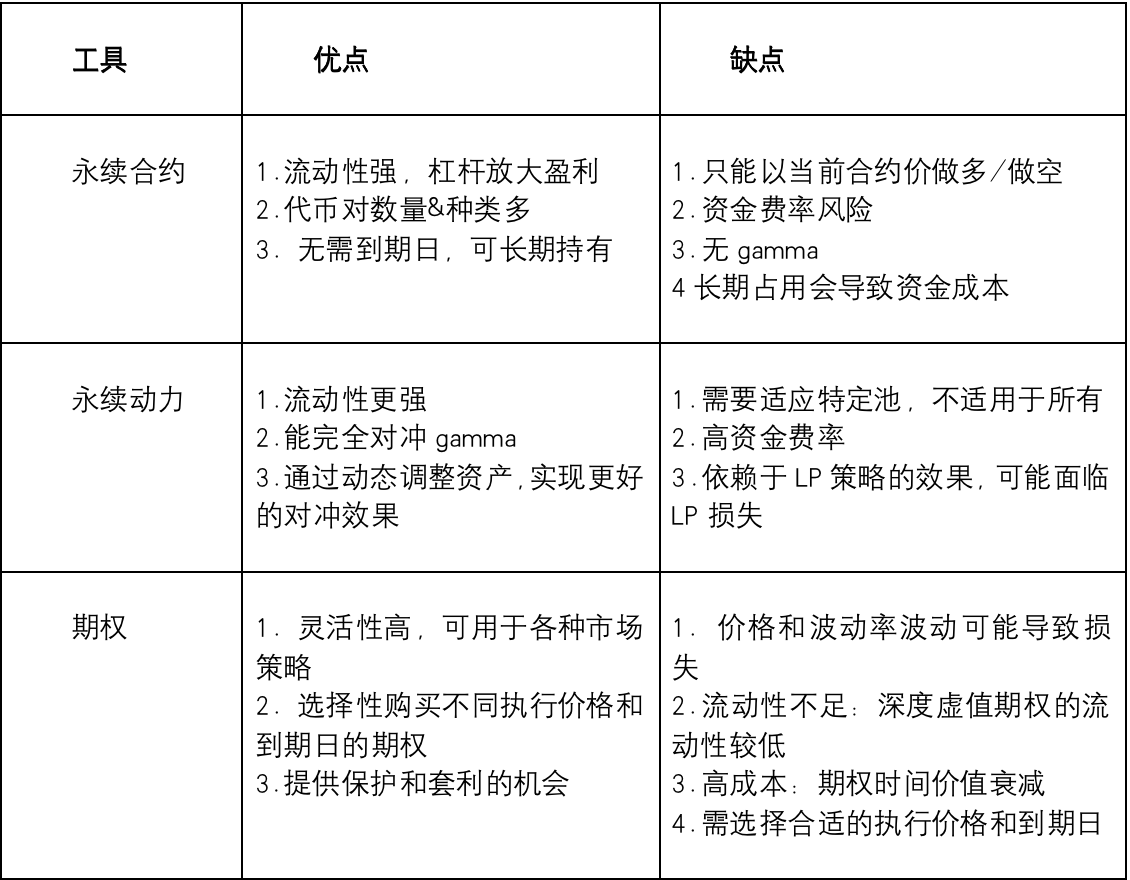
Conclusion
L’analyse ci-dessus montre clairement que pour éviter l’impact impermanent, chaque
Bienvenue dans la communauté officielle TechFlow
Groupe Telegram :https://t.me/TechFlowDaily
Compte Twitter officiel :https://x.com/TechFlowPost
Compte Twitter anglais :https://x.com/BlockFlow_News












