Comprendre en un article le protocole de compromis polynomial Brakedown dans FOAKS
TechFlow SélectionTechFlow Sélection
Comprendre en un article le protocole de compromis polynomial Brakedown dans FOAKS
Si les cryptographes n'avaient pas découvert la relation entre le produit tensoriel et l'évaluation polynomiale, il serait difficile d'imaginer l'apparition du protocole de compromis polynomial Brakedown, encore moins l'émergence d'Orion basé sur Brakedown ou de FOAK.
Rédaction : Kang Shuiyue, PDG de Fox Tech, et Meng Xuanji, scientifique en chef chez Fox Tech
Préambule : Si les cryptographes n'avaient pas découvert le lien entre le produit tensoriel (Tensor Product) et l'évaluation des polynômes, il serait difficile d'imaginer l'apparition du protocole de compromis polynomial Brakedown, ni par conséquent des nouveaux algorithmes rapides tels qu'Orion ou FOAKS fondés sur Brakedown.
Dans de nombreux systèmes de preuves à divulgation nulle reposant sur des compromis polynomiaux, différents protocoles de compromission sont utilisés. Selon une évaluation réalisée par Justin Thaler d'a16z dans son article de août 2022 intitulé « Measuring SNARK performance: Frontends, backends, and the future », bien que Brakedown présente une taille de preuve relativement élevée, c'est indéniablement le protocole de compromis polynomial le plus rapide actuellement disponible.
FRI, KZG et Bulletproof sont des protocoles de compromis polynomiaux plus courants, mais leur vitesse constitue un goulot d'étranglement. Des algorithmes comme Plonky utilisé par zkSync, Plonky 2 adopté par Polygon zkevm, ou Ultra-Plonk mis en œuvre par Scroll reposent tous sur le compromis polynomial KZG. Le prouveur (Prover) doit effectuer de nombreuses opérations FFT (Transformée de Fourier rapide) et MSM (Multiplication scalaire multiple), générant ainsi un fardeau computationnel considérable. Bien que la MSM puisse bénéficier d'accélération multithread, elle nécessite une grande quantité de mémoire et reste lente même avec un haut niveau de parallélisme. Quant à la FFT de grande taille, elle dépend fortement du réarrangement fréquent des données pendant l'exécution de l'algorithme, ce qui rend difficile son accélération distribuée sur plusieurs clusters informatiques.
C’est précisément grâce au protocole de compromis polynomial plus rapide Brakedown que la complexité de ces calculs a pu être fortement réduite.
FOAKS, ou Fast Objective Argument of Knowledge, est un cadre de système de preuve à divulgation nulle proposé par Fox Tech, basé sur Brakedown. FOAKS va encore plus loin qu’Orion en réduisant davantage les calculs FFT, avec pour objectif ultime de supprimer complètement les opérations FFT. En outre, FOAKS introduit une méthode de récursion de preuve entièrement nouvelle et particulièrement ingénieuse afin de réduire la taille des preuves. L’avantage principal du cadre FOAKS réside dans sa capacité à offrir un temps de génération de preuve linéaire tout en conservant une petite taille de preuve, ce qui le rend particulièrement adapté aux scénarios de zkRollup.
Nous allons maintenant détailler ci-dessous le protocole de compromis polynomial Brakedown utilisé par FOAKS.
En cryptographie, un protocole de compromis (Commitment) consiste pour un prouveur (Prover) à s'engager sur une valeur secrète donnée, produisant ainsi une valeur publique appelée « commitment ». Ce commitment possède deux propriétés essentielles : l'inaltéabilité (Binding) et la confidentialité (Hiding). Par la suite, le prouveur doit « ouvrir » ce commitment en envoyant le message correspondant au vérificateur, afin de prouver la cohérence entre le message initial et le commitment. Cette fonctionnalité partage de nombreux points communs avec les fonctions de hachage, bien que les protocoles de compromis reposent généralement sur des structures mathématiques issues de la cryptographie à clé publique. Un compromis polynomial (Polynomial Commitment) est une forme spécifique de compromis appliqué aux polynômes — autrement dit, la valeur engagée est elle-même un polynôme. De plus, un tel protocole inclut des algorithmes permettant d’évaluer le polynôme en un point donné et d’en fournir une preuve, ce qui fait des compromis polynomiaux des protocoles cryptographiques fondamentaux, au cœur de nombreux systèmes de preuve à divulgation nulle.
Dans les recherches récentes en cryptographie, la découverte d’un lien entre le produit tensoriel (Tensor Product) et l’évaluation des polynômes a conduit à toute une série de nouveaux protocoles de compromis polynomiaux. Brakedown en est un exemple emblématique.
Avant d’entrer dans les détails du protocole Brakedown, quelques notions préliminaires doivent être clarifiées : codes linéaires (Linear Code), fonctions de hachage résistantes aux collisions (Hash Function), arbres de Merkle (Merkle Tree), opération de produit tensoriel (Tensor Product), ainsi que la représentation sous forme de produit tensoriel de l’évaluation d’un polynôme.
Premièrement, définissons les codes linéaires (Linear Code). Un code linéaire de longueur de message k et de longueur de mot-code n est un sous-espace linéaire C ⊂ Fn, tel qu'il existe une injection du message vers le mot-code, appelée encodage, notée EC : Fk → C. Toute combinaison linéaire de mots-code donne également un mot-code. La distance entre deux mots-code u et v correspond à leur distance de Hamming, notée Δ(u, v).
La distance minimale est définie par d = minu,v Δ(u, v). Un tel code est noté [n, k, d] code linéaire, et la distance relative du code est donnée par d/n.
Deuxièmement, les fonctions de hachage résistantes aux collisions (Hash Function) et les arbres de Merkle (Merkle Tree).
On note H : { 0, 1 }2λ → { 0, 1 }λ une fonction de hachage. Un arbre de Merkle est une structure de données particulière permettant de s'engager sur 2d messages, produisant une valeur de hachage unique h. Pour ouvrir un message quelconque, d+1 valeurs de hachage sont nécessaires.
Un arbre de Merkle peut être vu comme un arbre binaire de profondeur d, où les L éléments de message m1, m2, ..., mL correspondent aux feuilles de l’arbre. Chaque nœud interne est obtenu en hachant ses deux nœuds fils. Pour ouvrir le message mi, il faut révéler le chemin menant de mi à la racine.
On utilise les notations suivantes :
-
h ← Merkle.Commit(m1,...,mL)
-
(mi, πi) ← Merkle.Open(m, i)
-
{ 0, 1 } ← Merkle.Verify(πi, mi, h)
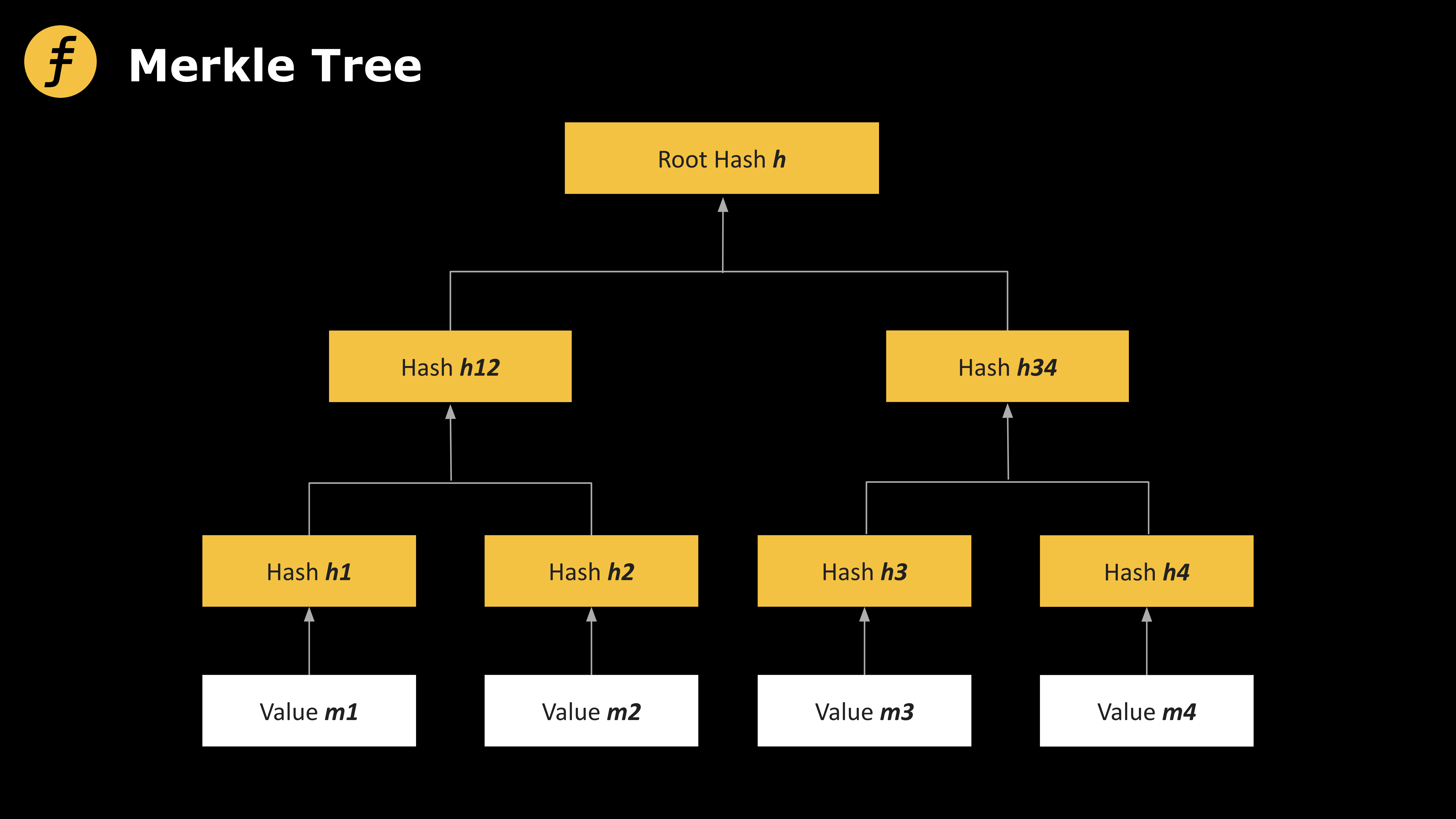
Figure 1 : Arbre de Merkle (Merkle Tree)
Il nous faut également comprendre comment fonctionne l’opération de produit tensoriel. Mathématiquement, un tenseur est une généralisation des vecteurs et matrices à des espaces de dimension supérieure, objet fondamental en mathématiques. Une discussion approfondie des tenseurs sort du cadre de cet article ; ici, nous ne présenterons que le produit tensoriel de vecteurs et de matrices.
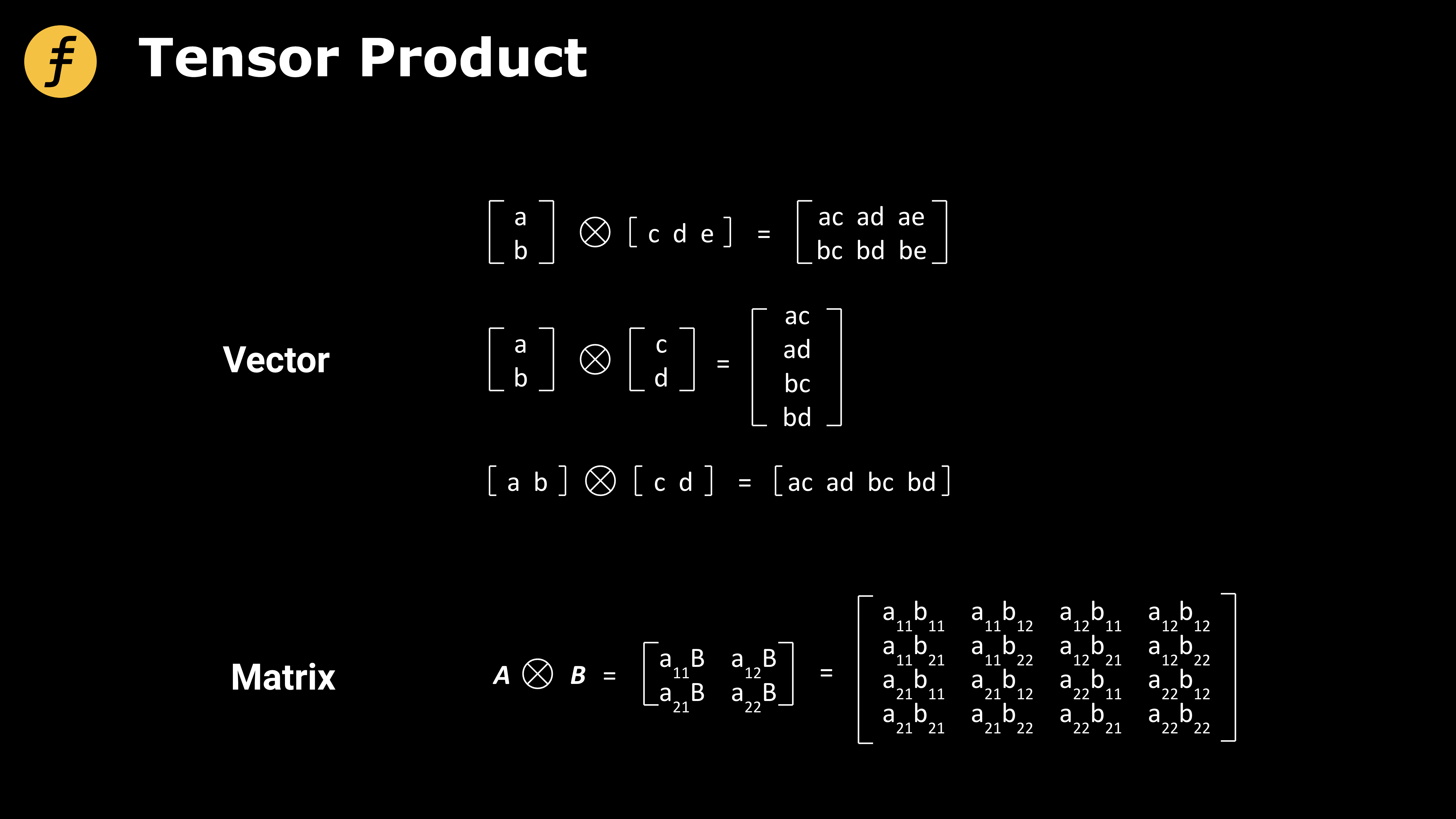
Figure 2 : Produit tensoriel de vecteurs et de matrices
Ensuite, nous devons connaître la représentation tensorielle de l’évaluation d’un polynôme.
Comme mentionné dans [GLS+], l’évaluation d’un polynôme peut être exprimée sous forme de produit tensoriel. Ici, nous considérons spécifiquement le compromis sur des polynômes multilinéaires.
Plus précisément, étant donné un polynôme, sa valeur en un vecteur x0, x1, ..., xlogN-1 peut s’écrire :
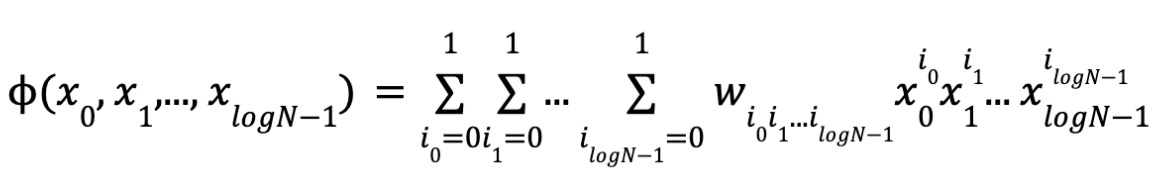
D’après la définition de multilinéarité, chaque variable apparaît au degré 0 ou 1. Ainsi, il y a N monômes et coefficients, ainsi que logN variables. Posons :
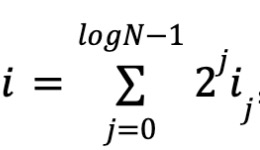
où i0i1...ilogN-1 est la représentation binaire de i. Soit w le vecteur des coefficients du polynôme,
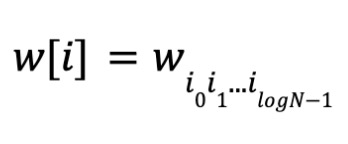
De même, on définit
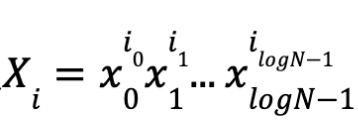
Posons
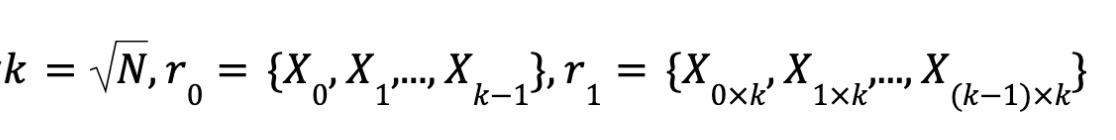
Ainsi, X = r0 ⊗ r1.
Par conséquent, l’évaluation du polynôme peut être exprimée sous forme de produit tensoriel : ϕ(x0, x1, ..., xlogN-1) = ⟨w, r0 ⊗ r1⟩.
Enfin, examinons le processus de Brakedown tel qu’utilisé dans FOAKS et Orion [XZS 22].
Tout d’abord, PC.Commit divise les coefficients w du polynôme en une matrice k×k, puis encode cette matrice (voir « connaissances préliminaires » concernant les codes linéaires), notée C2. Ensuite, un arbre de Merkle est construit pour chaque colonne C2[:, i]. Puis un second arbre de Merkle est construit à partir des racines de ces arbres de colonnes, servant de commitment final.
Dans la preuve d’évaluation, deux aspects doivent être prouvés : la proximité (Proximity) et la cohérence (Consistency). La proximité garantit que la matrice engagée est effectivement proche d’un mot-code encodé. La cohérence assure que y = ⟨w, r0 ⊗ r1⟩.
Vérification de proximité : Elle comporte deux étapes. D’abord, le vérificateur envoie un vecteur aléatoire Y0 au prouveur. Celui-ci calcule le produit scalaire entre Y0 et C1, c’est-à-dire une combinaison linéaire des lignes de C1 pondérée par les composantes de Y0. En raison des propriétés du code linéaire, CY0 est un mot-code de YY0. Ensuite, le prouveur doit prouver que CY0 provient bien du mot-code engagé. Pour cela, le vérificateur sélectionne aléatoirement t colonnes ; le prouveur ouvre ces colonnes et fournit les preuves de Merkle correspondantes. Le vérificateur vérifie que les produits scalaires entre ces colonnes et Y0 coïncident avec les positions correspondantes dans CY0. Comme démontré dans [BCG 20], si le code linéaire utilisé possède une distance relative constante, alors la matrice engagée est, avec une probabilité écrasante, proche d’un mot-code (« probabilité écrasante » signifiant que la probabilité contraire est négligeable).
Vérification de cohérence : Le processus est similaire à celui de la proximité, à ceci près que le vecteur aléatoire Y0 est remplacé directement par r0 dans la combinaison linéaire. De même, c1 est un mot-code linéaire du message y1, et on a
ϕ(x) = ⟨y1, r1⟩. Comme démontré dans [BCG 20], si la matrice engagée est proche d’un mot-code, alors la vérification de cohérence implique avec une probabilité écrasante que y = ϕ(x).
Voici le protocole Brakedown présenté sous forme de pseudocode :
Entrée publique : Le point d’évaluation X, décomposé comme produit tensoriel X = r0 ⊗ r1 ;
Entrée privée : Le polynôme ϕ, dont les coefficients sont notés w.
Soit C un code linéaire [n, k, d], EC : Fk → Fn la fonction d’encodage, N = k×k. Si N n’est pas un carré parfait, on le complète jusqu’au carré parfait suivant. On utilise une notation de style Python mat[:, i] pour désigner la i-ème colonne de la matrice mat.
-
fonction PC.Commit(ϕ) :
-
Interpréter w comme une matrice k×k. Le prouveur calcule localement l’encodage par code tensoriel C1, C2 ; C1 est une matrice k×n, C2 est une matrice n×n.
-
pour i ∈ [n] faire
-
Calculer la racine de l’arbre de Merkle Rooti = Merkle.Commit(C2[:, i])
-
Calculer la racine R = Merkle.Commit([Root0, ..., Rootn-1]), et renvoyer R comme commitment.
-
fonction PC.Prover(ϕ, X, R)
-
Le prouveur reçoit un vecteur aléatoire Y0 ∈ Fk du vérificateur
-
Proximité
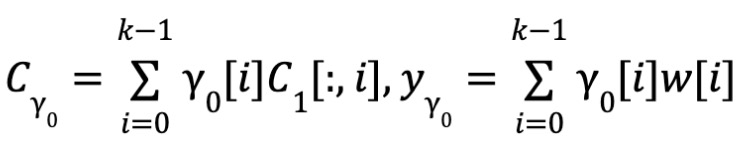
-
Cohérence
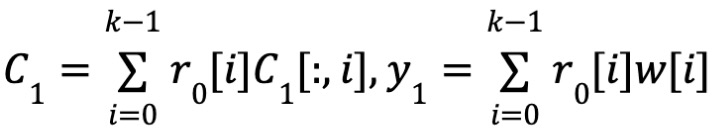
-
Le prouveur envoie C1, y1, C0, y0 au vérificateur.
-
Le vérificateur choisit aléatoirement un tableau t[n] noté Î et l’envoie au prouveur
-
pour idx ∈ Î faire
-
Le prouveur envoie C1[:, idx] et la preuve de Merkle de Rootidx pour C2[:, idx] sous R au vérificateur
-
fonction PC.VERIFY_EVAL(π, X, y=ϕ(X), R)
-
Proximité : ∀ idx ∈ Î, CY0[idx] == ⟨Y0, C1[:, idx]⟩ et EC(YY0) == CY0
-
Cohérence : ∀ idx ∈ Î, C1[idx] == ⟨Y0, C1[:, idx]⟩ et EC(Y1) == C1
-
y == ⟨r1, y1⟩
-
∀ idx ∈ Î, EC(C1[:, idx]) est cohérent avec Rootidx, et la preuve de l’arbre de Merkle de Rootidx est valide.
-
Accepter si toutes les conditions ci-dessus sont satisfaites. Sinon, rejeter.
Conclusion : Les compromis polynomiaux constituent une classe très importante de protocoles cryptographiques, largement utilisés dans divers systèmes cryptographiques, en particulier les systèmes de preuve à divulgation nulle. Cet article a détaillé le protocole de compromis polynomial Brakedown ainsi que les connaissances mathématiques associées. En tant que composant fondamental de FOAKS, Brakedown joue un rôle crucial dans l’amélioration significative des performances de mise en œuvre de FOAKS.
Références
-
[GLS+]: Alexander Golovnev, Jonathan Lee, Srinath Setty, Justin Thaler, and Riad S. Wahby. Brakedown: Linear-time and post-quantum snarks for r 1 cs. Cryptology ePrint Archive. https://ia.cr/2021/1043.
-
[XZS 22]: Xie T, Zhang Y, Song D. Orion: Zero knowledge proof with linear prover time[C]//Advances in Cryptology–CRYPTO 2022: 42nd Annual International Cryptology Conference, CRYPTO 2022, Santa Barbara, CA, USA, August 15–18, 2022, Proceedings, Part IV. Cham: Springer Nature Switzerland, 2022: 299-328. https://eprint.iacr.org/2022/1010
-
[BCG 20]: Bootle, Jonathan, Alessandro Chiesa, and Jens Groth. "Linear-time arguments with sublinear verification from tensor codes." Theory of Cryptography: 18th International Conference, TCC 2020, Durham, NC, USA, November 16–19, 2020, Proceedings, Part II 18. Springer International Publishing, 2020.
-
Justin Thaler d'A16z crypto, Measuring SNARK performance: Frontends, backends, and the future https://a16z crypto.com/measuring-snark-performance-frontends-backends-and-the-future/
-
Introduction au produit tensoriel : https://blog.csdn.net/chenxy_bwave/article/details/127288938
Bienvenue dans la communauté officielle TechFlow
Groupe Telegram :https://t.me/TechFlowDaily
Compte Twitter officiel :https://x.com/TechFlowPost
Compte Twitter anglais :https://x.com/BlockFlow_News