
비탈릭: 타원 곡선 페어링 탐구
글: 비탈릭 부테린
게시일: 2017년 1월 14일
결정론적 임계 서명(deterministic threshold signature), zk-SNARKs 및 기타 형태의 간단한 영지식 증명(zero-knowledge proof) 등 다양한 암호학 기반 시스템의 핵심 원리 중 하나는 타원 곡선 페어링(elliptic curve pairing)이다. 타원 곡선은 지난 30여 년간 암호화 및 디지털 서명과 같은 암호학 분야에서 광범위하게 사용되어 왔으며, '타원 곡선 페어링'(또는 쌍선형 맵)은 최근 그 위에 새롭게 도입된 개념으로, 암호화된 곱셈 연산을 가능하게 하여 타원 곡선 기반 프로토콜이 수행할 수 있는 작업의 범위를 크게 확장한다. 본 글에서는 타원 곡선 페어링에 대해 자세히 설명하고, 그 작동 방식을 간략히 소개한다.
이 개념은 실제로 매우 어렵기 때문에, 첫 번째 또는 열 번째 읽었을 때 완전히 이해하기를 기대하지 않는다. 하지만 이 글을 통해 적어도 일부 복잡성을 이해할 수 있기를 바란다.
타원 곡선 자체가 이미 쉽게 이해하기 어려운 주제이지만, 본문에서는 독자가 기본적인 작동 원리를 어느 정도 알고 있다고 가정한다. 만약 전혀 모르는 상태라면, 먼저 입문용 글을 추천한다.
요약하자면, 타원 곡선은 2차원 평면상의 점(x, y)인 ‘점(points)’라 불리는 수학적 개체와, 덧셈 및 뺄셈 등의 특수 공식(예: R = P + Q 계산)을 다룬다. 또한 점에 정수를 곱하는 것도 가능하다(예: P * n = P + P + … + P). 다만 n이 매우 클 경우 더 빠른 알고리즘이 존재한다.
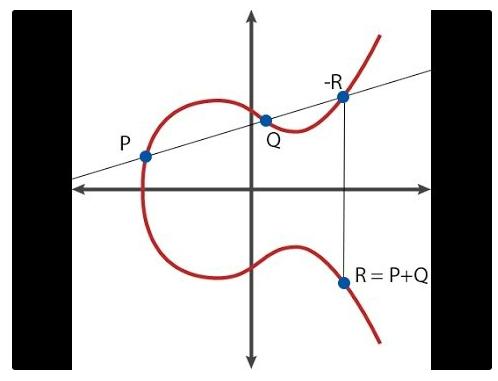
점의 덧셈이 그래프 상에서 어떻게 보이는지
덧붙여, ‘무한원점(O)’이라 불리는 특별한 점이 있으며, 이는 점 연산에서 항등원 역할을 한다. 즉 모든 점 P에 대해 P + O = P가 성립한다. 각 곡선은 ‘위수(order)’라 불리는 속성을 가지는데, 이는 모든 점 P에 대해 P * n = O가 되는 양의 정수 n이 존재한다는 의미다(따라서 P * (n + 1) = P이며, P * ((7*n) + 5) = P * 5 등도 성립함). 또한 사전에 합의된 ‘생성점(generator point) G’가 존재하는데, 이는 덧셈의 단위 원소로서 숫자 1을 나타내는 점이다. 이론적으로 곡선 상의 어떤 점도 생성원이 될 수 있지만, 중요한 것은 G가 통일되어 선택되어야 한다는 점이다.
페어링은 더 복잡한 종류의 등식을 검증할 수 있게 해준다. 예를 들어, P = G * p, Q = G * q, R = G * r일 때, p * q = r인지 여부를 확인하려면, P, Q, R 세 점의 좌표만 입력하면 된다. 이것은 마치 타원 곡선의 기본 보안이 무너진 것처럼 보일 수 있다. 왜냐하면 P의 좌표를 알면 p값이 유출되는 것처럼 보이기 때문이다. 그러나 사실 이 정보 유출은 매우 제한적이다. 정확히 말해, 판정형 디피-헬만 문제(Decisional Diffie-Hellman problem)는 쉬우나, 계산형 문제는 여전히 ‘계산상 불가능(computationally infeasible)’하다. 최소한 아는 것과 모르는 것 사이의 난이도 차이는 거의 없다고 보면 된다.
‘페어링’을 이해하는 세 번째 방법은 우리가 대부분의 사용 사례에서 가장 직관적인 관점일 수 있는데, 타원 곡선 상의 점을 일방향 암호 함수로 본다면(즉, encrypt(p) = p * G = P), 전통적인 타원 곡선 수학은 변수 간 선형 제약 조건을 검사할 수 있게 한다(P = G * p, Q = G * q, R = G * r이고, 5 * P + 7 * Q = 11 * R인지 검사하는 것은 사실상 5 * p + 7 * q = 11 * r인지 검사하는 것임). 반면 타원 곡선 페어링은 변수 간 이차 제약 조건을 검사할 수 있게 한다(e(P, Q) * e(G, G * 5) = 1인지 검사는 실은 p * q + 5 = 0인지 검사하는 것이다). 이차 제약 조건까지 가능해지면 결정론적 임계 서명, QAP(quadratic arithmetic programs, 일종의 영지식 증명) 등 흥미로운 응용이 가능해진다.
자, 이제 위에서 언급한 e(P, Q) 연산자는 정확히 무엇인가? 이것이 바로 ‘페어링’이다. 수학자들은 이를 가끔 ‘쌍선형 맵(bilinear map)’이라고도 부르며, 여기서 ‘쌍선형(bilinear)’은 다음 조건을 만족한다는 것을 의미한다:
e(P, Q + R) = e(P, Q) * e(P, R)
e(P + S, Q) = e(P, Q) * e(S, Q)
여기서 +와 *는 임의의 연산자일 수 있음에 주목해야 한다. 새로운 수학적 객체를 만들 때, 추상 대수학에서는 +와 *가 어떻게 ‘정의’되었는지보다는 우리가 익히 아는 연산 규칙과 일치하는지를 중요하게 본다. 예를 들어 a + b = b + a, (a * b) * c = a * (b * c), (a * c) + (b * c) = (a + b) * c 등이다.
만약 지금 P, Q, R, S가 단순한 숫자라면, 페어링 함수는 아주 쉽게 구성할 수 있다: e(x, y) = 2^(xy)로 정의할 수 있다. 그러면 다음과 같이 된다:
e(3, 4 + 5) = 2^(3 * 9) = 2²⁷
e(3, 4) * e(3, 5) = 2^(3 * 4) * 2^(3 * 5) = 2¹² * 2¹⁵ = 2²⁷
실제로 쌍선형이다!
그러나 이렇게 간단한 페어링은 암호학에는 적합하지 않다. 정수 상에서 정의된 수학적 구조를 분석하는 것은 너무 쉽기 때문이다. 정수는 나눗셈, 로그 등 많은 연산을 쉽게 만들며, ‘공개키’나 ‘일방향 함수’라는 개념도 없다. 게다가 위에서 설명한 페어링은 역연산이 가능하다: x와 e(x, y)를 알면 나눗셈과 로그를 통해 y를 계산할 수 있다. 우리가 원하는 수학적 구조는 가능한 한 ‘블랙박스’에 가까워야 한다: 덧셈, 뺄셈, 곱셈, 나눗셈은 할 수 있지만 그 이상은 못하도록 말이다. 이때 타원 곡선과 타원 곡선 페어링이 등장한다.
사람들은 실제로 타원 곡선 상의 두 점 P와 Q를 입력으로 받아 F_p¹²의 원소로 매핑하는 쌍선형 맵 e(P, Q)를 설계할 수 있다는 것을 발견했다(적어도 특정 상황에서 충분히 작동하며, 이는 곡선의 세부사항에 따라 달라질 수 있고, 뒤에서 다시 언급됨). 그러나 이를 실현하는 수학적 배경은 극도로 복잡하다.
먼저 소수체(prime fields)와 확장체(extension fields)를 소개하겠다. 위의 그래프는 보기 좋지만, 곡선의 방정식이 실수 위에서 정의되었다고 가정할 때만 그렇게 보인다. 만약 실제로 암호학에서 실수를 사용한다면, 로그를 통해 ‘되돌릴’ 수 있어 모든 것이 무용지물이 되며, 실수를 저장하는 데 필요한 공간도 무한할 수 있다. 따라서 우리는 실수체 대신 소수체 상의 숫자를 사용한다.
소수체는 0, 1, 2, …, (p−1)로 구성된 집합이며, 여기서 p는 소수이고, 연산은 다음과 같이 정의된다:
a + b: (a + b) % p
a * b: (a * b) % p
a - b: (a - b) % p
a / b: (a * b^(p-2)) % p
기본적으로 모든 연산은 모듈러(modulo) p에서 수행된다(모듈러 연산에 대한 소개 참고). 나눗셈은 예외다. 일반적으로 3/2는 정수가 아니지만, 우리는 정수만 다루고 싶으므로, x * 2 = 3이 되는 정수 x를 찾는다. 여기서 *는 위에서 정의한 모듈러 곱셈이다. 다행히 페르마 소정리 덕분에 지수 형식의 나눗셈 정의가 가능하지만, 더 빠른 방법으로는 확장 유클리드 알고리즘을 사용하는 것이다. p = 7이라고 가정하면 아래와 같은 예가 있다:
2 + 3 = 5 % 7 = 5
4 + 6 = 10 % 7 = 3
2 - 5 = -3 % 7 = 4
6 * 3 = 18 % 7 = 4
3 / 2 = (3 * 2^5) % 7 = 5
5 * 2 = 10 % 7 = 3
이러한 연산을 직접 해보면 일관성이 있으며, 모든 일반적인 규칙을 만족하는 것을 알 수 있다. 마지막 두 예는 (a / b) * b = a임을 보여주며, (a + b) + c = a + (b + c), (a + b) * c = a * c + b * c 등 고등학교에서 배운 다른 대수 등식들도 계속 성립한다. 실제로 사용되는 타원 곡선에서는 점과 방정식이 일반적으로 소수체 상에서 연산된다.
이제 확장체(extension field)에 대해 살펴보자. 당신은 아마 이전에 확장체를 본 적이 있을 것이다. 수학 교과서에서 가장 흔한 예는 복소수체인데, 실수체에 sqrt(-1) = i라는 새로운 원소를 추가하여 확장한 것이다. 간단히 말해, 확장체는 기존 체에 새로운 원소를 ‘발명’하고, 이 새로운 원소와 기존 원소 간의 관계를 정의하는 것이다(위 예에서는 i² + 1 = 0). 이 관계식은 기존 숫자로는 만족되지 않아야 하며, 이 새로운 원소를 기존 원소들의 모든 선형 결합(linear combination)으로 구성된 집합에 추가함으로써 새로운 집합을 구성한다.
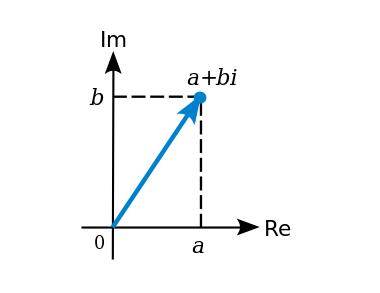
소수체에도 확장을 적용할 수 있다. 예를 들어, 모듈러 7의 소수체에 앞서 언급한 i를 추가하면 다음과 같다:
(2 + 3i) + (4 + 2i) = 6 + 5i
(5 + 2i) + 3 = 1 + 2i
(6 + 2i) * 2 = 5 + 4i
4i * (2 + i) = 3 + i
마지막 등식은 다소 이해하기 어려울 수 있다. 우선 좌변의 곱셈을 분배하여 4i * 2 + 4i * i로 만들면 8i - 4가 된다. 모듈러 7 환경에서 이 값은 i + 3이 된다. 나눗셈의 경우는 다음과 같다:
a / b : (a * b^(p^2-2)) % p
여기서 페르마 소정리의 지수는 p에서 p²로 바뀌며, 확장 유클리드 알고리즘을 사용하면 더 효율적으로 계산할 수 있다. 체 내 임의의 원소 x에 대해 x^(p² − 1) = 1이므로, (p² − 1)을 ‘체의 승법군의 위수(order of the multiplicative group)’라고 부른다.
실수체의 경우, 대수학의 기본 정리에 의해 이차 확장(복소수체)이 완비(algebraically closed)임이 보장된다—즉, 모든 새로운 원소 j와 기존 복소수 사이의 다항식 관계를 만족하는 원소가 이미 그 안에 존재하므로 더 이상 확장할 수 없다(역주: 실수체는 완비적이지만 확장 가능하며, 여기서 ‘완비’는 ‘대수적으로 닫힘’을 의미함). 그러나 소수체에서는 이러한 문제가 없으며, 삼차 확장(cubic extension)(새 원소 w와 기존 원소 사이의 관계가 삼차 다항식으로 주어져 1, w, w²이 선형 독립), 고차 확장, 또는 확장을 반복하는 것도 가능하다. 타원 곡선은 이러한 모듈러 연산 기반의 복소수 상에 구축된다.
이러한 수학적 구조를 코드로 구현하는 데 관심이 있다면, 소수체 및 확장체를 구현한 예제를 참고할 수 있다.
다시 타원 곡선 페어링으로 돌아오자. 타원 곡선 페어링(여기서 논의하는 페어링은 그중 하나일 뿐이지만, 논리는 유사함)은 G2 × G1 → Gt로의 사상이며, 다음을 만족한다:
- G1은 y² = x³ + b 형태의 방정식을 만족하는 타원 곡선이며, 점의 x, y 좌표는 모두 F_p의 원소이다(즉 일반적인 숫자이지만, 산술 연산은 모듈러 소수에서 수행됨).
- G2 역시 동일한 곡선을 따르지만, G2의 점들의 x, y 좌표는 F_p¹²의 원소이다(앞서 언급한 복소수; 우리는 12차 다항식 w¹² − 18w⁶ + 82 = 0을 만족하는 마법의 숫자 w를 정의함).
- Gt는 타원 곡선 연산 결과가 이루는 집합이다. 우리가 다루는 곡선에서 Gt는 F_p¹²이다(G2와 동일한 복소수 사용).
핵심적으로 만족해야 할 성질은 쌍선형성인데, 이 맥락에서 다음과 같이 표현된다:
e(P, Q + R) = e(P, Q) * e(P, R)
e(P + Q, R) = e(P, R) * e(Q, R)
(역주: 여기서의 쌍선형성은 정확히는 ‘정수 위의 쌍선형성(bilinearity over ℤ)’이며, 이는 다루는 타원 곡선 상의 점들이 정수점이고, 곱셈과 덧셈이 정수 연산 후 모듈러 연산으로 정의되기 때문에 자연스럽게 일부 선형 성질을 만족함)
페어링 함수를 선택할 때 두 가지 중요한 기준이 있다:
- 연산이 충분히 효율적이어야 함(예: 모든 점에 대해 이산 로그를 직접 계산한 후 모두 곱하는 간단한 페어링 방법을 생각할 수 있지만, 이는 타원 곡선 암호를 깨는 것만큼 어렵기 때문에 실용적이지 않음).
- 비퇴화(non-degeneracy)여야 함(e(P, Q) = 1로 정의할 수도 있지만, 이는 특히 유용한 페어링이 아님).
그렇다면 우리는 어떻게 이를 달성할 수 있을까?
페어링 함수가 작동하게 하는 수학적 배경은 매우 어렵고, 지금까지 살펴본 내용보다 더 진보한 대수학을 필요로 하지만, 개략적으로 설명하겠다. 먼저 ‘약수(divisor)’의 개념을 정의해야 한다. 이는 타원 곡선 상의 점에 작용하는 함수들을 표현하는 또 다른 방법이다. 함수의 약수는 그 함수가 몇 개의 영점(zero)과 무한대 값을 가지는지를 계산한다. 좀 더 명확히 이해하기 위해 몇 가지 예를 살펴보자. 점 P = (P_x, P_y)를 선택하고, 다음 함수를 고려하자:
f(x, y) = x − P_x
이 함수의 약수는 [P] + [−P] − 2 * [O]이다(여기서 대괄호는 함수의 영점이나 무한대 값을 가지는 점의 집합을 나타내며, 점 자체를 의미하지는 않는다; [P] + [Q]와 [P + Q]는 다르다). 이유는 다음과 같다:
- x가 P_x일 때 x − P_x = 0이므로, 이 함수는 P에서 0이 된다.
- −P는 P와 x좌표가 같으므로, 이 함수는 −P에서도 0이 된다.
- x가 무한대로 갈 때 함수 값도 무한대로 간다. 따라서 O에서 무한대 값을 갖는다고 말한다. 이 무한원점을 두 번 계산하므로 O에 -2의 계수를 붙인다(음수는 영점과 구분하기 위한 것이며, 2는 두 번 계산되기 때문).
계산상의 이유는 대략 다음과 같다: 곡선 방정식이 x³ = y² + b이므로, x가 커질수록 y²도 비슷한 규모가 되려면 y는 x의 약 1.5배 속도로 증가해야 한다. 따라서 x만 포함하는 선형 함수는 무한대 항의 계수가 2이며, y를 포함하면 계수는 3이 된다.
이제 직선의 함수를 생각해보자:
ax + by + c = 0
여기서 a, b, c는 점 P와 Q를 지나도록 선택된다. 타원 곡선 덧셈의 작동 방식에 따라, 이 직선은 반드시 −P−Q도 지나야 한다. 무한대 방향으로 갈 때 x와 y 모두에 의존하므로, 약수는 [P]+ [Q] + [−P−Q] − 3 * [O]이다.
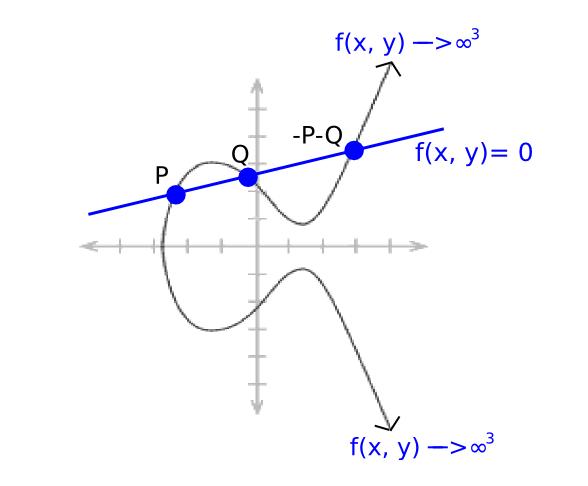
모든 ‘유리 함수(rational function)’(점의 좌표에 유한 번의 사칙연산을 적용하여 정의된 함수)는 어떤 약수와 유일하게 대응되며, 최대한 상수배 만큼의 차이만 있다(즉, 두 함수 F와 G가 동일한 약수를 가지면, 상수 k가 존재하여 F = G * k임).
임의의 두 함수 F와 G에 대해, (F * G)의 약수는 F와 G의 약수의 합과 같다(수학 서적에서는 (F * G) = (F) + (G)로 표기). 예를 들어 f(x, y) = P_x − x이면, (f³) = 3 * [P] + 3 * [−P] − 6 * [O]; P와 −P가 세 번 등장하는 이유는 특정한 수학적 의미에서 f³가 ‘세 배 빠르게’ 0에 접근하기 때문이다.
약수의 ‘대괄호’를 제거하고 점들을 연산하면 그 결과는 반드시 O가 된다는 정리가 있음을 주목하라([P] + [Q] + [−P−Q] − 3 * [O]를 연산하면 P + Q − P − Q − 3 * O = O). 그리고 이러한 성질을 갖는 모든 약수는 어떤 함수의 약수이다.
이제 Tate 페어링을 살펴보자. 다음 약수로 정의된 함수들을 고려하자:
- (F_P) = n * [P] − n * [O], 여기서 n은 G1의 위수, 즉 모든 P에 대해 n * P = O가 성립함.
- (F_Q) = n * [Q] − n * [O]
- (g) = [P + Q] − [P] − [Q] + [O]
이제 곱 F_P * F_Q * g^n을 살펴보자. 그 약수는 다음과 같다:
n * [P] − n * [O] + n * [Q] − n * [O] + n * [P + Q] − n * [P] − n * [Q] + n * [O]
정리하면 깔끔하게:
n * [P + Q] − n * [O]
이 약수의 형태가 F_P와 F_Q의 약수와 일치함에 주목하라. 따라서 F_P * F_Q * g^n = F_(P + Q)이다.
이제 ‘최종 지수승(final exponentiation)’이라 불리는 연산을 추가로 수행한다. 앞서 계산된 결과(F_P, F_Q 등)를 z = (p¹² − 1) / n의 지수로 거듭제곱한다. 여기서 p¹² − 1은 F_p¹²의 승법군의 위수(즉, 모든 x ∈ F_p¹²에 대해 x^(p¹² − 1) = 1). 이 지수를 이미 n의 거듭제곱인 결과에 적용하면, 어떤 원소의 (p¹² − 1)제곱이 되어 결과는 1이 된다. 따라서 최종 지수 단계 후 g^n은 소거되고, F_P^z * F_Q^z = F_(P + Q)^z를 얻게 된다. 이로부터 쌍선형성의 일부 성질이 도출된다.
이제 두 매개변수 모두에서 쌍선형인 함수를 구성하고자 한다면, 더 복잡한 수학이 필요하며, F_P뿐만 아니라 F_P의 약수까지 계산해야 하며, 이를 통해 완전한 Tate 페어링을 얻게 된다. 더 많은 결론을 증명하려면 ‘선형 동치(linear equivalence)’ 및 Weil 상반성(Weil reciprocity) 등의 개념을 이해해야 한다. 이러한 개념의 자세한 내용은 여기와 여기에서 볼 수 있다.
실제로는 Tate 페어링의 변형인 Optimal Ate Pairing이 구현되어 있다. 이 코드에서는 밀러 알고리즘(Miller's algorithm)을 사용하여 F_p를 계산한다.
사실, 이러한 페어링을 사용하는 것은 양날의 검과 같다: 한편으로는 다양한 프로토콜을 구현할 수 있게 해주는 반면, 다른 한편으로는 어떤 타원 곡선을 선택할지 신중해야 한다는 의미이기도 하다.
모든 타원 곡선은 embedding degree라 불리는 값을 가지는데, 이는 p^k − 1이 n의 배수가 되는 최소의 정수 k이다(p는 체의 소수, n은 곡선의 위수). 앞서 언급한 체에서는 k = 12이며, 전통적인 타원 곡선 암호학(페어링을 고려하지 않는 경우)에서 사용되는 체의 embedding degree는 일반적으로 매우 크며, 페어링을 계산하는 것이 계산상 불가능할 정도이다. 그러나 주의하지 않으면 k = 4 또는 심지어 k = 1인 체를 구성할 수도 있다.
k = 1일 경우, 타원 곡선 상의 ‘이산 로그 문제’(P = G * p인 점만 알고 있을 때 p를 계산하는 문제; 즉 타원 곡선의 개인키를 해킹하려 할 때 풀어야 하는 문제)가 F_p 상의 비교적 쉬운 문제로 축소될 수 있다(이 방법을 MOV 공격이라 한다). embedding degree가 12 이상인 타원 곡선을 사용하면 이러한 축소가 불가능하거나, 축소된 문제가 공개키로부터 개인키를 일반적인 방법으로 계산하는 것만큼 어렵게 보장할 수 있다. 현재 모든 표준 곡선 파라미터는 이 문제의 영향을 받지 않도록 철저히 검토되었다.
TechFlow 공식 커뮤니티에 오신 것을 환영합니다
Telegram 구독 그룹:https://t.me/TechFlowDaily
트위터 공식 계정:https://x.com/TechFlowPost
트위터 영어 계정:https://x.com/BlockFlow_News
















