どのように巧妙な再帰的証明スキームを設計できるか？

2023.02.21

共有先

TechFlow厳選深潮セレクト

どのように巧妙な再帰的証明スキームを設計できるか？

zkRollupおよびzkEVMの分野で遭遇するほぼすべての課題は、本質的にアルゴリズムの問題である。ZKPハードウェアアクセラレーションが繰り返し言及される主な理由は、現在のアルゴリズムが一般的に遅いからである。

2023.02.21 - 05:10:14

ZKP

Web3業界の深掘り報道に専念し潮流を洞察

執筆：Fox Tech CTO 林彦熹、Fox Tech 最高科学責任者孟铉济

序論：zkRollupおよびzkEVM分野で直面するほぼすべての難題は、本質的にアルゴリズムに関する問題である。ZKPハードウェアアクセラレーションが繰り返し注目される主な理由は、現在のアルゴリズムが一般的に遅いためである。「アルゴリズム不足をハードウェアで補う」という不都合な状況を避けるためにも、我々は根源的なアルゴリズムの改善に取り組むべきである。優れた再帰的証明スキームを設計することが、この問題を解決する鍵となる。

スマートコントラクトの進化に伴い、ますます多くのWeb3アプリケーションが登場しており、イーサリアムなどの従来型Layer1の取引量は急速に増加し、いつでも混雑が発生する可能性がある。Layer1が提供するセキュリティを維持しつつ、より高い効率を得る方法は、今まさに解決が求められている課題である。

イーサリアムの場合、zkRollupはゼロ知識証明（ZKP）アルゴリズムを基盤構成要素として用い、元々Layer1上で実行される高コストな計算処理をオフチェーンに移転し、その正しさの証明のみをオンチェーンに提出する。この分野には主にStarkWare、zkSync、Scroll、Fox Techといったプロジェクトが存在する。

実際、zkRollupの設計では効率性に対する要求が非常に高く、提出される証明データのサイズは可能な限り小さくすべきである。これによりLayer1の計算負荷を軽減できるため、各zkRollupプロジェクトは証明アルゴリズムやアーキテクチャの改良に取り組んでいる。たとえばFox Techは最新のゼロ知識証明アルゴリズムを統合し、最適な証明時間と証明サイズを実現する独自の証明アルゴリズムFOAKSを開発した。

また、証明の検証フェーズにおいて、最も単純な方法は線形に証明を生成し、一つずつ検証していくことである。効率を向上させるため、複数の証明を一つにまとめる「証明集約（Proof Aggregation）」がよく用いられる。

直感的に言えば、zkEVMによって生成された証明の検証は線形プロセスであり、検証者（Verifier）はそれぞれの証明を順番に検証しなければならない。しかし、この方式は効率が低く、通信オーバーヘッドも大きい。zkRollupの文脈では、検証側のコストが高くなるほど、Layer1での計算量が増え、結果としてGas手数料が上昇する。

ここで一例を見てみよう。Aliceは今月の1日から7日まで毎日Fox公園に行ったことを世界に証明したいとする。そのため、彼女は1日から7日までの毎日、当日の新聞を持って公園で写真を撮る。この7枚の写真をまとめたものが一つの証明となる。

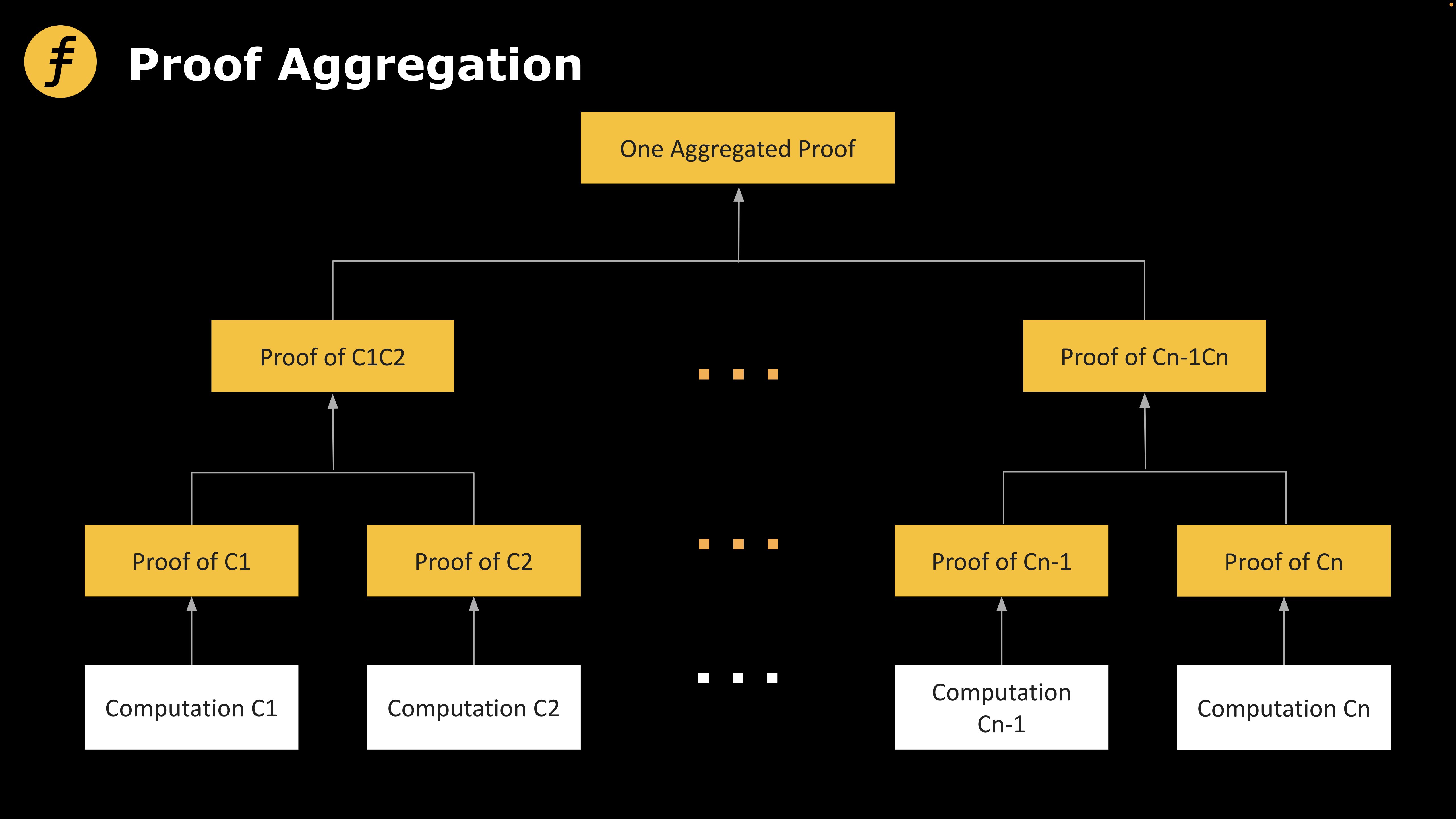
どのようにして卓越した証明再帰スキームを設計するか？

図1：一般的な証明集約スキーム

上の例で、7枚の写真をそのまま封筒に入れることが、直感的な意味での証明集約に相当する。これは実際には異なる証明を連結し、先頭から順に線形に検証するプロセスに対応している。すなわち、最初の証明を検証し、次に二番目の証明を検証し…という流れである。しかし、この方法では証明のサイズも時間も変わらず、個別に証明・検証する場合と同様の効果しか得られない。対数レベルの空間圧縮を実現するには、以下に述べる再帰的証明（Proof Recursion）を用いる必要がある。

Halo2およびSTARKが採用する証明再帰スキーム

再帰的証明とは何かをより明確にするために、先ほどの例に戻ってみよう。

Aliceの7枚の写真は、それぞれ7つの証明に相当する。これらを統合することを考える。Aliceは1日に写真を撮り、2日にはその1日の写真と2日の新聞を持って写真を撮る。3日には2日に撮った写真と3日の新聞を持ってさらに写真を撮る。このようにして、7日には6日に撮った写真と7日の新聞を持って最終の一枚を撮影する。他の人々はこの7日目の一枚の写真を見るだけで、1日から7日までAliceが公園に行ったことを検証できる。つまり、当初の7枚の証明写真が一枚に圧縮されたのである。このプロセスにおける重要な技術は、「写真を含む写真」という再帰的な入れ子構造であり、複数の写真を並べて一緒に撮影するのとは本質的に異なる。

zkRollupにおける再帰的証明技術は、証明サイズを大幅に圧縮できる。具体的には、各取引ごとに一つの証明が生成される。元の取引計算回路をC0、その正当性の証明をP0、P0を検証する計算プロセスをV0とする。証明者（Prover）はV0自体を回路に変換し、これをC0'と記す。このとき、別の取引の証明計算回路C1に対して、C0'とC1の回路を統合できる。この統合された回路の正当性証明P1を検証することで、両方の取引の正当性が同時に検証されたことになり、圧縮が実現される。

このプロセスを振り返ると、圧縮の原理は「証明の検証プロセス自体を回路に変換し、『証明の証明』を生成する」ことにあり、これは理論的に無限に再帰可能な操作である。このため、再帰的証明と呼ばれる。

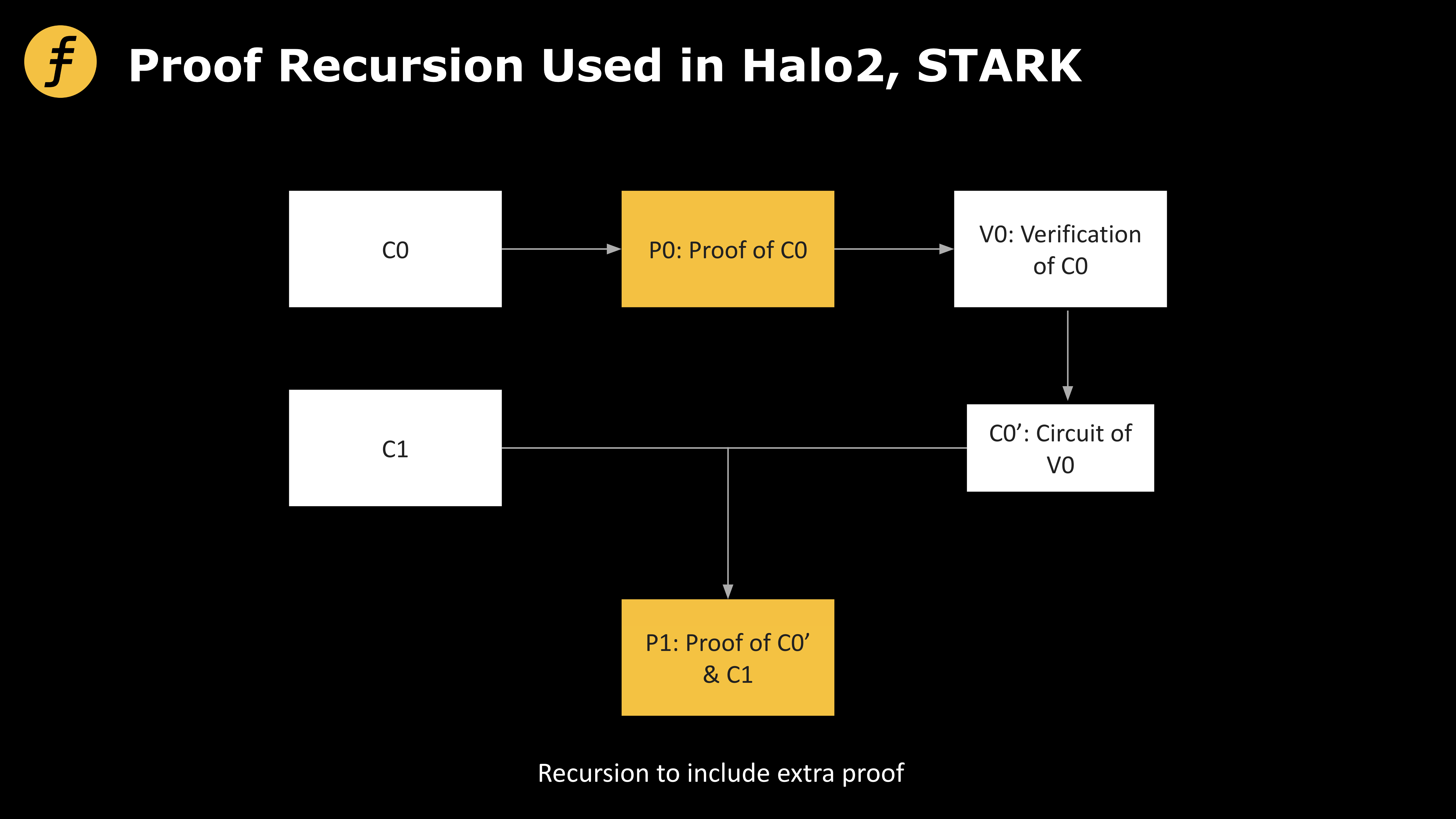
どのようにして卓越した証明再帰スキームを設計するか？

図2：Halo2およびStarkが使用する再帰的証明スキーム

Halo2およびSTARKが採用するProof Recursionスキームは、複数の証明を並列に生成し、それらを一つに統合することで、単一の証明値の検証を通じて複数の取引の正当性を同時に検証できるようにする。これにより計算コストが圧縮され、システム全体の効率が大きく向上する。

しかし、このような最適化は依然として特定のゼロ知識証明アルゴリズムの上位レイヤーに留まっている。さらなる効率化を達成するには、より根本的な下位層での最適化と革新が必要となる。Foxが設計したFOAKSアルゴリズムは、再帰的概念を「一つの証明の内部」に適用することで、この課題に取り組んでいる。

FOAKSが採用する証明再帰スキーム

Fox TechはzkEVMベースのzkRollupプロジェクトである。その証明システムでも再帰的証明の技術が使われるが、その内容は前述の再帰方式とは異なり、主な違いは「一つの証明の内部で再帰（Recursion）の考え方が使われる点」にある。Foxが採用する再帰的証明が、証明対象の問題を段階的に簡略化し、最終的に十分簡単な問題に帰着させるという核心思想を示すために、もう一つ例を挙げよう。

前述の例で、Aliceは写真を撮ることで自分が特定の日にFox公園に行ったことを証明した。これに対してBobは別の提案をする。彼は「Aliceが公園に行ったことを証明する問題は、『Aliceの携帯電話が公園に行ったこと』を証明する問題に還元できる」と考える。そして、「携帯電話が公園に行ったこと」の証明はさらに「その携帯の位置情報が公園の範囲内にあったこと」の証明に還元できる。したがって、Aliceが公園にいたことを証明するには、公園にいるときに自分の携帯で位置情報を送信すればよい。こうすることで、証明のサイズは一枚の写真（高次元データ）から3次元のデータ（経度、緯度、時刻）にまで削減され、コストが有効に節約される。この例は完全に適切ではないかもしれない。なぜなら、誰かが「携帯が公園にあっても本人が行ったとは限らない」と反論するかもしれないからだ。しかし実際の状況では、このような還元プロセスは数学的に厳密に行われる。

具体的には、Foxの再帰的証明は回路レベルでの再帰を意味する。ゼロ知識証明を行う際、証明対象の問題を回路として表現し、その回路から満たすべき等式を導出する。これらの等式が満たされていることを示す代わりに、さらにそれらの等式自体を新たな回路として表現し、同じプロセスを繰り返す。最終的に証明すべき等式が十分に簡単になった時点で、それを直接証明することが容易になる。

このプロセスからわかるように、これはより本来の「再帰」の意味に近い。ただし、すべてのアルゴリズムでこの再帰技術が使えるわけではない。仮に一回の再帰でO(n)の複雑さを持つ証明がO(f(n))に変化し、再帰プロセス自体の計算複雑度がO(g(n))であるとすると、一回目の再帰後の総計算複雑度はO1(n) = O(f(n)) + O(g(n))、二回目はO2(n) = O(f(f(n))) + O(g(n)) + O(g(f(n)))、三回目はO3(n) = O(f(f(f(n)))) + O(g(n)) + O(g(f(n))) + O(g(f(f(n)))) となり、以降も同様に続く。したがって、あるkについてOk(n) < O(n)が成り立つようなfとgの関数関係が存在する場合にのみ、この再帰技術は有効に機能する。Foxはこの条件を満たすように再帰技術を活用し、証明の複雑度を効果的に圧縮している。

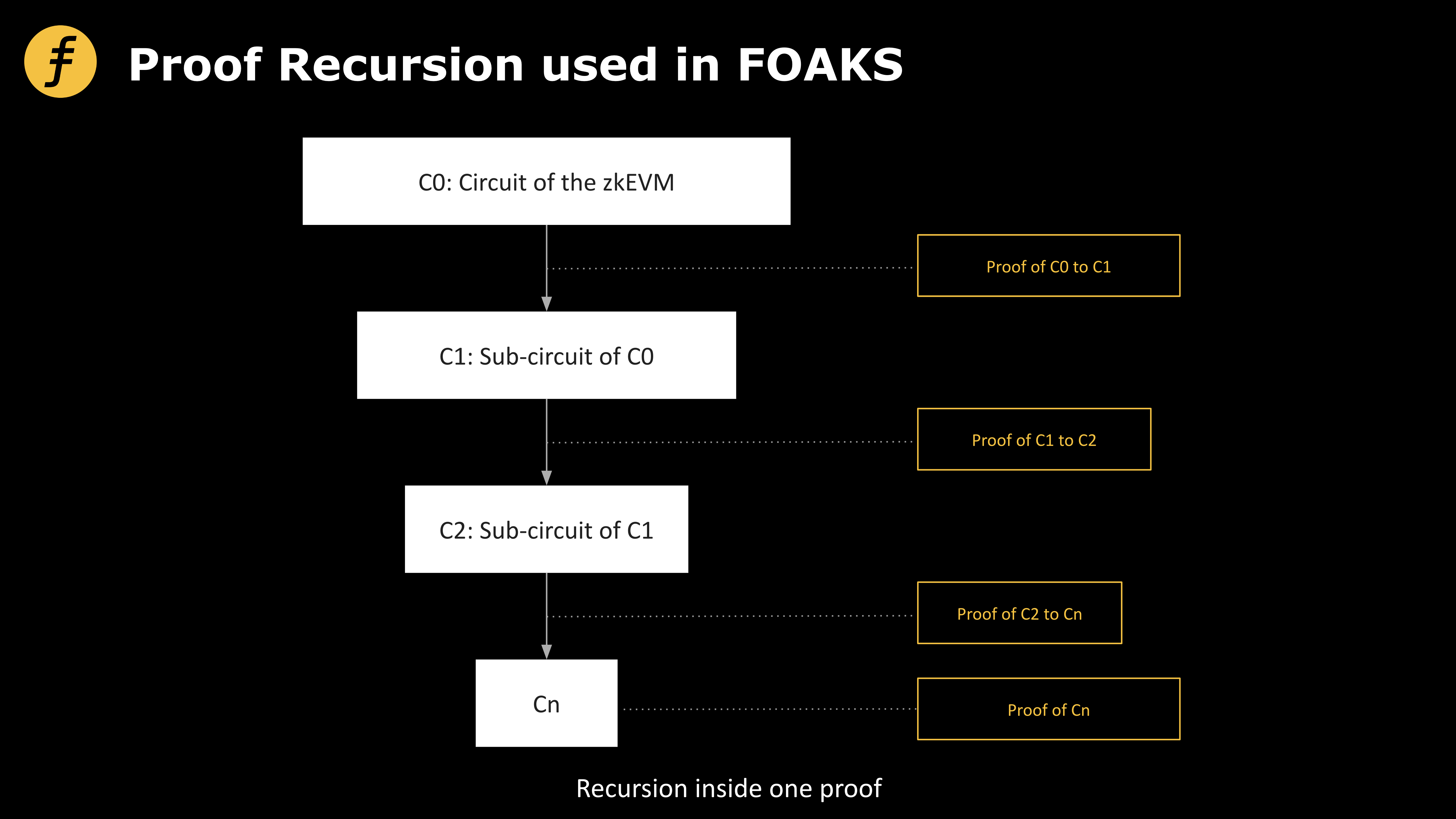
どのようにして卓越した証明再帰スキームを設計するか？

図3：ZK-FOAKSが採用する再帰的証明スキーム

結語

証明の複雑度は、ゼロ知識証明の応用において常に最も重要な要素の一つである。証明対象がますます複雑になるにつれて、この特性の重要性はさらに高まる。特にzkEVMのような巨大なZK応用シナリオでは、証明の複雑度が製品のパフォーマンスとユーザー体験に決定的な影響を与える。多くの証明複雑度低減手法の中でも、中核アルゴリズムの最適化が最も重要である。Foxは最先端のアルゴリズムに基づき、卓越した再帰的証明スキームを設計し、この技術を用いてzkEVMに最も適したZK-FOAKSアルゴリズムを構築した。これにより、zkRollup分野における高性能ソリューションとしての地位を築くことが期待される。