
Vitalik : Complexité encapsulée et complexité systémique dans la conception des protocoles
TechFlow SélectionTechFlow Sélection

Vitalik : Complexité encapsulée et complexité systémique dans la conception des protocoles
Soutenir modérément la complexité d'emballage, et exercer notre jugement dans des situations spécifiques.
Rédaction : Vitalik Buterin, co-fondateur d'Ethereum
Traduction : Nanfeng, Unitimes
L'un des objectifs principaux de la conception du protocole Ethereum est de minimiser la complexité : rendre le protocole aussi simple que possible, tout en permettant à la blockchain de remplir efficacement ce qu’un réseau blockchain doit faire. Le protocole Ethereum est encore loin d’être parfait à cet égard, notamment parce que de nombreuses parties ont été conçues entre 2014 et 2016, une période où notre compréhension était bien plus limitée. Néanmoins, nous continuons activement à travailler pour réduire autant que possible cette complexité.
Cependant, l’un des défis liés à cet objectif est que la complexité est difficile à définir. Parfois, il faut choisir entre deux options introduisant des types différents de complexité, avec des coûts distincts. Comment trancher ?
Un outil intellectuel puissant permettant une réflexion plus fine sur la complexité consiste à distinguer ce que nous appelons la complexité encapsulée (encapsulated complexity) et la complexité systémique (systemic complexity).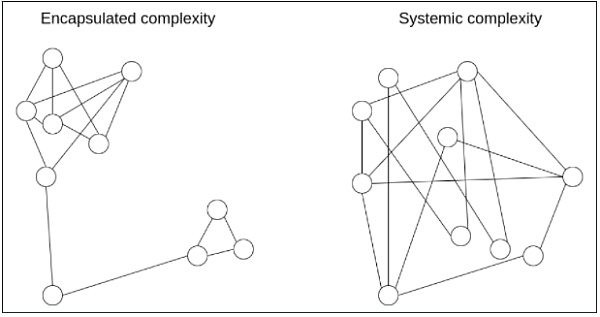
La « complexité encapsulée » apparaît lorsqu’un sous-système est internement complexe, mais expose à l’extérieur une interface simple. La « complexité systémique » se produit lorsque les différentes parties d’un système ne peuvent pas être clairement séparées et interagissent de manière compliquée entre elles.
Voici quelques exemples.
Signatures BLS vs signatures Schnorr
Les signatures BLS et les signatures Schnorr sont deux schémas cryptographiques courants pouvant être construits à partir de courbes elliptiques.
Mathématiquement, les signatures BLS semblent très simples :
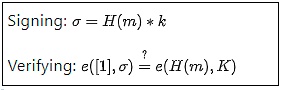
H est une fonction de hachage, m un message, k et K respectivement une clé privée et une clé publique. Jusque-là, tout va bien. Cependant, la véritable complexité se cache dans la définition de la fonction e : les couplages de courbes elliptiques (elliptic curve pairings), l’une des parties les plus ardues des mathématiques en cryptographie.
Considérons maintenant les signatures Schnorr. Elles reposent uniquement sur des courbes elliptiques élémentaires. Toutefois, la logique de signature et de vérification est un peu plus complexe :

Alors… quel type de signature est « plus simple » ? Cela dépend de ce qui vous importe ! Les signatures BLS présentent une grande complexité technique, mais celle-ci est entièrement cachée dans la définition de la fonction e. Si vous traitez e comme une boîte noire, alors les signatures BLS sont en réalité très simples. En revanche, les signatures Schnorr ont une complexité globale moindre, mais comportent davantage d’éléments pouvant interagir subtilement avec le monde extérieur.
Par exemple :
-
Créer une multi-signature BLS (combinaison de deux clés k1 et k2) est simple : il suffit de calculer σ1+σ2. Mais la multi-signature Schnorr nécessite deux tours d’interaction et doit gérer des attaques délicates de type Key Cancellation.
-
Les signatures Schnorr nécessitent une génération de nombres aléatoires, contrairement aux signatures BLS.
Les couplages de courbes elliptiques constituent souvent une puissante « éponge à complexité », car ils contiennent une grande quantité de complexité encapsulée, mais permettent d’obtenir des solutions ayant moins de complexité systémique. Cela s’applique également au domaine des engagements polynomiaux : comparez la simplicité des engagements KZG (nécessitant des couplages) à la logique interne plus complexe des arguments de produit scalaire (inner product arguments), qui n’en nécessitent pas.
Cryptographie vs cryptoéconomie
Un choix important dans la conception de nombreuses blockchains oppose la cryptographie (cryptography) à la cryptoéconomie (cryptoeconomics). Dans les rollups par exemple, cela revient souvent à choisir entre des preuves de validité (c’est-à-dire les ZK-SNARKs) et des preuves de fraude.
Les ZK-SNARKs sont techniquement complexes. Bien que l’idée fondamentale derrière leur fonctionnement puisse être expliquée en un article, implémenter concrètement un ZK-SNARK pour vérifier un calcul donné implique une complexité bien supérieure à celle du calcul lui-même (c’est pourquoi les preuves ZK-SNARKs pour l’EVM sont encore en développement, tandis que les preuves de fraude pour l’EVM sont déjà en phase de test). Mettre en œuvre efficacement une preuve ZK-SNARK exige la conception de circuits optimisés pour des cas spécifiques, l’utilisation de langages de programmation inhabituels, ainsi que de nombreux autres défis. En revanche, les preuves de fraude sont simples en soi : si quelqu’un lance un défi, on exécute simplement le calcul directement sur la chaîne. Pour améliorer l’efficacité, on peut parfois ajouter un schéma de recherche binaire, mais cela n’ajoute guère de complexité.
Bien que les ZK-SNARKs soient complexes, leur complexité est encapsulée. En revanche, la faible complexité des preuves de fraude est systémique. Voici quelques exemples de complexités systémiques introduites par les preuves de fraude :
-
Elles exigent une ingénierie minutieuse des incitations pour éviter le dilemme du vérificateur.
-
Si mises en œuvre dans le consensus, elles nécessitent un type de transaction supplémentaire pour les preuves de fraude, tout en tenant compte de ce qui se passe si plusieurs participants tentent simultanément de soumettre une telle preuve.
-
Elles dépendent d’un réseau synchrone.
-
Elles permettent que des attaques par censure soient utilisées à des fins de vol.
-
Les rollups basés sur les preuves de fraude requièrent des fournisseurs de liquidité pour prendre en charge les retraits instantanés.
Pour ces raisons, même d’un point de vue purement lié à la complexité, une solution purement cryptographique basée sur les ZK-SNARKs pourrait s’avérer plus sûre à long terme : les ZK-SNARKs ont des composants plus complexes, ce dont certains acteurs doivent tenir compte lorsqu’ils choisissent cette option ; mais les ZK-SNARKs ont moins de risques latents, auxquels tout le monde doit faire attention.
Autres exemples
-
PoW (consensus de Nakamoto) : faible complexité encapsulée, car le mécanisme est très simple et facile à comprendre, mais complexité systémique plus élevée (ex. : attaques de minage égoïste).
-
Fonctions de hachage : forte complexité encapsulée, mais propriétés très faciles à comprendre, donc faible complexité systémique.
-
Algorithmes de permutation aléatoire : un algorithme peut être internement complexe (ex. : Whisk), tout en garantissant une forte randomisation aisément analysable ; ou bien internement simple, mais produisant une randomisation faible et difficile à analyser (donc complexité systémique).
-
Extraction de valeur par les mineurs (MEV) : un protocole suffisamment robuste pour supporter des transactions complexes peut être très simple en interne, mais ces transactions complexes peuvent avoir des effets systémiques complexes sur les incitations du protocole, en proposant des blocs de façon très atypique.
-
Arbres Verkle : les arbres Verkle ont effectivement une certaine complexité encapsulée, nettement plus élevée que celle des arbres de hachage Merkle classiques. Toutefois, du point de vue systémique, ils offrent une interface aussi propre et simple que celle d'une simple table clé-valeur. Le principal « fuite » de complexité systémique provient de la possibilité pour un attaquant de manipuler l'arbre Verkle afin qu'une valeur particulière ait une branche très longue ; mais ce risque est identique pour les arbres Merkle.
Comment arbitrer ?
Souvent, l’option qui présente une complexité encapsulée plus faible est aussi celle qui a une complexité systémique plus faible, rendant le choix évident. Mais parfois, il faut opérer un choix difficile entre deux formes de complexité. Il devrait désormais être clair que la complexité encapsulée est moins dangereuse. Le risque lié à la complexité systémique ne dépend pas simplement de la longueur des spécifications : un petit fragment de code de 10 lignes pouvant interagir avec d'autres parties du système peut être plus complexe qu'une fonction de 100 lignes traitée comme une boîte noire.
Toutefois, cette préférence pour la complexité encapsulée a ses limites. Des bogues peuvent apparaître dans n’importe quel morceau de code, et plus celui-ci est volumineux, plus la probabilité d’erreur tend vers 1. Parfois, lorsque l’on doit interagir avec un sous-système d’une nouvelle manière imprévue, une complexité initialement encapsulée peut devenir systémique.
Un exemple est l’arbre d’état à deux niveaux actuellement utilisé dans Ethereum, composé d’un arbre d’objets de comptes, chaque objet de compte possédant à son tour son propre arbre de stockage.
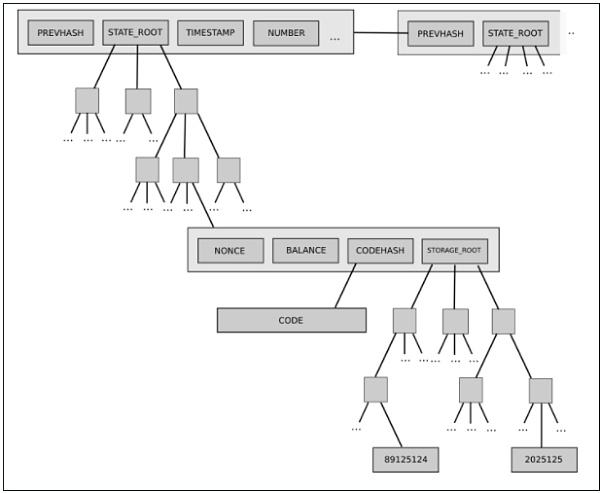
Cette structure arborescente est complexe, mais au départ, sa complexité semblait bien encapsulée : le reste du protocole interagit avec l’arbre comme avec un stockage clé/valeur lisible/inscriptible, sans avoir à se soucier de sa construction interne.
Or, par la suite, cette complexité s’est révélée avoir des effets systémiques : le fait qu’un compte puisse posséder un arbre de stockage arbitrairement grand signifie qu’il est impossible de prévoir de manière fiable la taille d’une partie donnée de l’état (par exemple, « tous les comptes commençant par 0x1234 »). Cela rend plus difficile la segmentation de l’état en plusieurs parties, compliquant ainsi la conception des protocoles de synchronisation et les tentatives de distribution des processus de stockage. Pourquoi la complexité encapsulée est-elle devenue systémique ? Parce que l’interface a changé. Quelle est la solution ? La proposition actuelle de migration vers les arbres Verkle inclut également un passage à une conception arborescente unique et équilibrée.
En fin de compte, dans chaque situation donnée, la question de savoir quel type de complexité est préférable n’a pas de réponse simple. Le mieux que nous puissions faire est de favoriser modérément la complexité encapsulée, sans excès, et d’exercer notre jugement au cas par cas. Parfois, sacrifier un peu de complexité systémique pour réduire fortement la complexité encapsulée est effectivement la meilleure approche. D’autres fois, on peut même se tromper sur ce qui est encapsulé ou non. Chaque cas est différent.
Bienvenue dans la communauté officielle TechFlow
Groupe Telegram :https://t.me/TechFlowDaily
Compte Twitter officiel :https://x.com/TechFlowPost
Compte Twitter anglais :https://x.com/BlockFlow_News
















