
Vitalik : Explorer les couplages de courbes elliptiques
TechFlow SélectionTechFlow Sélection

Vitalik : Explorer les couplages de courbes elliptiques
Les courbes elliptiques sont largement utilisées depuis plus de trente ans dans des applications cryptographiques telles que le chiffrement et la signature numérique.
Rédaction : Vitalik Buterin
Date de publication : 14 janvier 2017
L'une des constructions fondamentales derrière de nombreuses infrastructures cryptographiques, telles que les « signatures seuils déterministes », les zk-SNARKs et d'autres formes plus simples de preuves à divulgation nulle, est le concept de couplage sur courbes elliptiques. Les courbes elliptiques sont utilisées depuis plus de trente ans dans diverses applications cryptographiques comme le chiffrement ou les signatures numériques. Les « couplages sur courbes elliptiques » (ou applications bilinéaires) constituent une nouveauté récente qui ajoute la multiplication cryptographique aux possibilités offertes par les protocoles basés sur les courbes elliptiques, élargissant considérablement leurs fonctionnalités. Cet article présente en détail les couplages sur courbes elliptiques et explique brièvement leur fonctionnement.
Ce concept étant particulièrement difficile, il ne faut pas s'attendre à le comprendre pleinement du premier coup, ni même après dix lectures. Toutefois, j'espère que cet article pourra vous en révéler quelques subtilités.
Les courbes elliptiques elles-mêmes sont déjà un sujet complexe. Cet article suppose donc généralement une certaine familiarité avec leur fonctionnement. Si ce n'est pas votre cas, je recommande vivement de commencer par lire l'article susmentionné.
En résumé, les courbes elliptiques manipulent des objets mathématiques appelés « points », concrètement des couples (x, y) dans un plan bidimensionnel, munis de formules spéciales d'addition et de soustraction (par exemple R = P + Q). On peut aussi multiplier un point par un entier (P * n = P + P + … + P), bien qu'un algorithme beaucoup plus efficace existe lorsque n est grand.
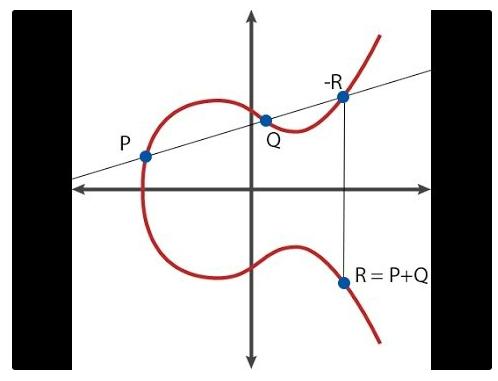
Voici à quoi ressemble graphiquement l’addition de points
Il existe également un point spécial appelé « point à l'infini » (O), qui joue le rôle d'élément neutre dans les opérations : pour tout point P, on a P + O = P. Une courbe possède également une caractéristique appelée « ordre », c’est-à-dire un entier positif n tel que, pour tout point P, P * n = O (et donc P * (n + 1) = P, P * ((7*n) + 5) = P * 5, etc.). Enfin, il existe un « point générateur » G prédéfini, choisi comme unité additive représentant le nombre 1. En théorie, n'importe quel point de la courbe pourrait servir de générateur, mais il est crucial que G soit uniformément convenu.
Le couplage permet de vérifier des équations plus complexes : par exemple, si P = G * p, Q = G * q, R = G * r, alors on peut vérifier si p * q = r simplement à partir des coordonnées des points P, Q et R. Cela semble au premier abord violer la sécurité fondamentale des courbes elliptiques, car connaître les coordonnées de P semblerait révéler directement la valeur de p. Pourtant, cette fuite d'information est extrêmement limitée — précisément, le problème de Diffie-Hellman décisionnel devient facile, mais sa version calculatoire reste « computationnellement infaisable ». La difficulté est au moins comparable à celle du cas où aucune information n’est révélée.
Une troisième manière de comprendre les « couplages », souvent la plus intuitive dans les contextes d'utilisation discutés ici, consiste à voir les points sur une courbe elliptique comme le résultat d'une fonction de chiffrement à sens unique (c’est-à-dire encrypt(p) = p * G = P). Alors que les mathématiques classiques des courbes elliptiques permettent de vérifier des contraintes linéaires entre variables (vérifier 5*P + 7*Q = 11*R revient à tester 5*p + 7*q = 11*r), les couplages permettent de vérifier des contraintes quadratiques (vérifier e(P, Q) * e(G, G*5) = 1 revient à tester p*q + 5 = 0). Cette capacité à gérer des relations quadratiques suffit à rendre possible des applications avancées comme les signatures seuils déterministes ou les QAP (programmes arithmétiques quadratiques, une forme de preuve à divulgation nulle).
La question maintenant est : qu'est-ce exactement que cette opération e(P, Q) introduite ci-dessus ? C’est ce qu’on appelle un « couplage ». Les mathématiciens parlent parfois d’« application bilinéaire », où « bilinéaire » signifie essentiellement qu’elle satisfait les conditions suivantes :
e(P, Q + R) = e(P, Q) * e(P, R)
e(P + S, Q) = e(P, Q) * e(S, Q)
Notez que les symboles + et * peuvent désigner n'importe quelle opération ; en algèbre abstraite, lorsqu'on définit un nouvel objet mathématique, peu importe comment on nomme les opérations + et *, du moment qu'elles respectent les règles usuelles : a + b = b + a, (a * b) * c = a * (b * c), (a * c) + (b * c) = (a + b) * c.
Si P, Q, R, S étaient simplement des nombres, construire un tel couplage serait très simple : on pourrait définir e(x, y) = 2^(xy). On obtient alors :
e(3, 4 + 5) = 2^(3 * 9) = 2²⁷
e(3, 4) * e(3, 5) = 2^(3 * 4) * 2^(3 * 5) = 2¹² * 2¹⁵ = 2²⁷
C’est bien bilinéaire !
Cependant, un tel couplage trop simple n’est pas adapté à la cryptographie, car analyser des objets mathématiques simples sur les entiers est aisé : les propriétés des entiers rendent faciles des opérations comme la division ou le logarithme. De plus, les entiers ne permettent pas de modéliser des concepts comme les clés publiques ou les fonctions à sens unique. En outre, le couplage décrit ci-dessus est inversible : connaissant x et e(x, y), on peut retrouver y par division et logarithme. Ce que nous recherchons, c’est une structure mathématique aussi proche que possible d’une « boîte noire » : on peut y effectuer des additions, soustractions, multiplications, divisions, mais rien de plus. C’est là qu’interviennent les courbes elliptiques et leurs couplages.
On a découvert qu’il était possible de définir des applications bilinéaires sur les points des courbes elliptiques — autrement dit, concevoir une fonction e(P, Q) prenant deux points P et Q sur une courbe elliptique et produisant un élément dans F_p¹² (au moins dans ce cas particulier, bien que cela puisse varier selon les courbes, comme mentionné plus tard). Cependant, les mathématiques sous-jacentes sont extrêmement complexes.
Commençons par introduire les corps premiers (prime fields) et les extensions de corps (extension fields). La courbe illustrée plus haut est belle, mais elle suppose que l’équation de la courbe est définie sur les nombres réels. En cryptographie, utiliser les réels serait catastrophique : on pourrait utiliser les logarithmes pour « remonter », ruinant toute sécurité, sans parler du fait que stocker des réels nécessiterait une mémoire potentiellement infinie. Nous utilisons donc des nombres dans un corps fini.
Un corps premier est l’ensemble {0, 1, 2, ..., p−1}, où p est un nombre premier, muni des opérations suivantes :
a + b : (a + b) % p
a * b : (a * b) % p
a - b : (a - b) % p
a / b : (a * b^(p-2)) % p
Toutes les opérations se font modulo p (voir introduction aux arithmétiques modulaires). La division est un cas particulier : 3/2 n’est pas un entier, mais nous voulons rester dans les entiers. Nous cherchons donc un entier x tel que x * 2 ≡ 3 mod p, où * désigne la multiplication modulaire définie ci-dessus. Heureusement, grâce au petit théorème de Fermat, la formule exponentielle fonctionne. Une méthode encore plus rapide utilise l’algorithme d’Euclide étendu. Exemples avec p = 7 :
2 + 3 = 5 % 7 = 5
4 + 6 = 10 % 7 = 3
2 - 5 = -3 % 7 = 4
6 * 3 = 18 % 7 = 4
3 / 2 = (3 * 2^5) % 7 = 5
5 * 2 = 10 % 7 = 3
En expérimentant ces opérations, on constate qu’elles sont cohérentes et satisfont toutes les règles habituelles. Les deux derniers exemples montrent que (a / b) * b = a. On vérifie aussi (a + b) + c = a + (b + c), (a + b) * c = a * c + b * c, ainsi que toutes les autres identités algébriques familières. Dans les courbes elliptiques utilisées en pratique, les points et les équations sont généralement définis sur des corps premiers.
Passons maintenant aux extensions de corps. Vous avez probablement déjà rencontré une extension : les nombres complexes, obtenus en ajoutant √(-1) = i au corps des réels. Une extension de corps consiste à « inventer » un nouvel élément sur un corps existant, puis à définir une relation entre ce nouvel élément et les éléments existants (dans cet exemple, i² + 1 = 0). Cette relation ne doit pas être satisfaite par les éléments existants. L’ensemble résultant est constitué de toutes les combinaisons linéaires de l’ancien corps avec ce nouvel élément.
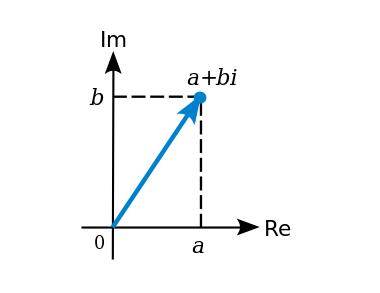
On peut aussi étendre un corps premier ; par exemple, ajouter i modulo 7 donne :
(2 + 3i) + (4 + 2i) = 6 + 5i
(5 + 2i) + 3 = 1 + 2i
(6 + 2i) * 2 = 5 + 4i
4i * (2 + i) = 3 + i
La dernière équation peut sembler obscure : elle vient de distribuer 4i*(2+i) = 8i + 4i² = 8i - 4. Ensuite, modulo 7, cela devient i + 3. Pour la division :
a / b : (a * b^(p²-2)) % p
Ici, l’exposant de Fermat passe de p à p², bien que l’algorithme d’Euclide étendu reste plus efficace. Comme tout élément x du corps vérifie x^(p²⁻¹) = 1, on appelle (p²⁻¹) « l’ordre du groupe multiplicatif du corps ».
Pour les réels, le théorème fondamental de l’algèbre garantit que son extension quadratique (les complexes) est algébriquement close — elle ne peut pas être étendue davantage, car toute nouvelle relation polynomiale aurait déjà une solution dans le corps. Mais les corps premiers n’ont pas cette propriété : on peut les étendre cubiquement (avec un élément w satisfaisant un polynôme de degré 3, donc 1, w, w² sont indépendants), à des degrés supérieurs, voire itérer les extensions. Les courbes elliptiques sont construites sur ces sortes de « complexes modulaires ».
Pour ceux intéressés par l’implémentation, voici un exemple de code implémentant corps premiers et extensions.
Revenons aux couplages. Le couplage elliptique (un type parmi d’autres, mais logiquement similaire) est une application G2 × G1 → Gt telle que :
- G1 est une courbe elliptique dont les points satisfont y² = x³ + b, avec x, y dans F_p (des entiers modulo un nombre premier).
- G2 est une autre courbe elliptique similaire, mais ses points ont des coordonnées x, y dans F_p¹² (les « complexes » mentionnés plus haut, avec un élément w vérifiant w¹² − 18w⁶ + 82 = 0).
- Gt est l’ensemble d’arrivée du couplage. Ici, Gt = F_p¹² (même corps que pour G2).
La propriété principale requise est la bilinéarité, qui ici signifie :
e(P, Q + R) = e(P, Q) * e(P, R)
e(P + Q, R) = e(P, R) * e(Q, R)
(Note : cette bilinéarité est techniquement « sur ℤ », car les points sont des entiers et les opérations sont des combinaisons linéaires modulo p.)
Deux critères importants pour choisir un couplage :
- Efficacité : on pourrait prendre les logarithmes discrets de tous les points, les multiplier, mais cela serait aussi coûteux que casser la cryptographie sur courbes elliptiques — donc inacceptable.
- Non-dégénérescence : définir e(P, Q) = 1 est simple, mais inutile.
Alors, comment faire ?
Les mathématiques derrière les couplages sont très difficiles, nécessitant de l’algèbre avancée, mais voici un aperçu. D’abord, introduisons la notion de « diviseur », une façon alternative de représenter des fonctions agissant sur les points d’une courbe elliptique. Un diviseur compte les zéros et les pôles (valeurs infinies) d’une fonction. Pour clarifier, prenons un exemple. Soit P = (P_x, P_y), et considérons :
f(x, y) = x − P_x
Son diviseur est [P] + [−P] − 2*[O] (les crochets indiquent l’appartenance à l’ensemble des zéros/pôles, pas le point lui-même ; [P]+[Q] ≠ [P+Q]). Pourquoi ?
- f(P) = 0 car x = P_x
- f(−P) = 0 car −P a même abscisse que P
- Quand x → ∞, f → ∞, donc un pôle en O. Ce pôle compte double, d’où le coefficient −2 (signe négatif pour pôle, 2 pour multiplicité).
Explication technique : l’équation y² = x³ + b implique que y croît comme x^(3/2). Donc une fonction en x seule a un pôle de multiplicité 2, en y de multiplicité 3.
Considérons maintenant une droite :
ax + by + c = 0
choisie pour passer par P et Q. Par définition de l’addition elliptique, elle passe aussi par −P−Q. Dépendant à la fois de x et y, son diviseur est [P] + [Q] + [−P−Q] − 3*[O].
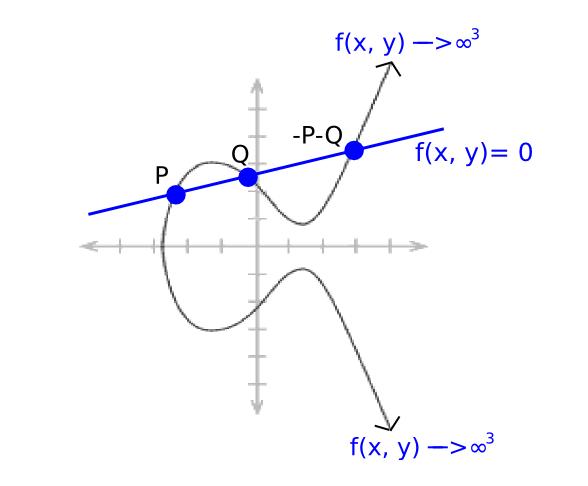
On sait que toute « fonction rationnelle » (composée d’opérations élémentaires sur les coordonnées) correspond à un diviseur unique, à une constante multiplicative près (si deux fonctions ont même diviseur, elles diffèrent d’un facteur constant).
Pour deux fonctions F et G, le diviseur de (F*G) est la somme des diviseurs (F) + (G). Ainsi, si f(x,y) = P_x − x, alors (f³) = 3*[P] + 3*[−P] − 6*[O], car f³ tend vers 0 « trois fois plus vite ».
Un théorème important : si on « retire les crochets » d’un diviseur, la somme pondérée des points vaut toujours O (ex. [P]+[Q]+[−P−Q]−3*[O] → P+Q−P−Q−3O = O). Et tout diviseur ayant cette propriété provient d’une fonction.
Voyons maintenant le couplage de Tate. Considérons les fonctions définies par leurs diviseurs :
- (F_P) = n*[P] − n*[O], où n est l’ordre de G1 (donc n*P = O ∀P)
- (F_Q) = n*[Q] − n*[O]
- (g) = [P+Q] − [P] − [Q] + [O]
Considérons F_P * F_Q * g^n. Son diviseur est :
n*[P] − n*[O] + n*[Q] − n*[O] + n*[P+Q] − n*[P] − n*[Q] + n*[O]
ce qui se simplifie en :
n*[P+Q] − n*[O]
Ce diviseur correspond à celui de F_(P+Q). Donc F_P * F_Q * g^n = F_(P+Q).
Appliquons ensuite une « exponentiation finale » : élever le résultat (F_P, F_Q, etc.) à la puissance z = (p¹² − 1)/n, où p¹² − 1 est l’ordre du groupe multiplicatif de F_p¹² (ainsi, ∀x ∈ F_p¹², x^(p¹²⁻¹) = 1). Notons que si un élément est une puissance n-ième, son z-ième pouvoir sera (quelque chose)^(p¹²⁻¹) = 1. Après cette étape, g^n disparaît, et on obtient F_P^z * F_Q^z = F_(P+Q)^z, montrant partiellement la bilinéarité.
Pour construire une fonction bilinéaire en deux arguments, il faut des mathématiques plus sophistiquées, allant au-delà du simple calcul de F_P. Cela conduit au couplage complet de Tate. Des notions comme l’« équivalence linéaire » ou la « réciprocité de Weil » sont nécessaires pour des preuves rigoureuses. Plus de détails ici et là.
Une version modifiée, le couplage Ate optimal, est implémentée ici. Le code utilise l’algorithme de Miller pour calculer F_P.
En réalité, utiliser de tels couplages est une arme à double tranchant : d’un côté, ils permettent de nouveaux protocoles ; de l’autre, ils imposent une vigilance accrue dans le choix des courbes.
Chaque courbe elliptique a un « degré d’immersion » k : le plus petit entier tel que pᵏ − 1 soit divisible par n (p est le nombre premier du corps, n l’ordre de la courbe). Dans notre exemple, k = 12. En cryptographie classique (sans couplage), k est très grand, rendant le calcul de couplages impossible. Mais par négligence, on pourrait avoir k = 4 ou même k = 1.
Quand k = 1, le « problème du logarithme discret » (retrouver p à partir de P = G * p, équivalent à casser la clé privée) se ramène à un problème plus simple dans F_p (attaque MOV). Utiliser une courbe avec k ≥ 12 garantit que cette réduction est impossible, ou que le problème réduit reste aussi dur que le cas initial. Tous les paramètres standards actuels sont soigneusement vérifiés contre ce risque.
Bienvenue dans la communauté officielle TechFlow
Groupe Telegram :https://t.me/TechFlowDaily
Compte Twitter officiel :https://x.com/TechFlowPost
Compte Twitter anglais :https://x.com/BlockFlow_News
















