
Vitalik: Khám phá phép ghép cặp trên đường cong elliptic
Tuyển chọn TechFlowTuyển chọn TechFlow

Vitalik: Khám phá phép ghép cặp trên đường cong elliptic
Đường cong elliptic đã được sử dụng rộng rãi trong hơn ba mươi năm qua trong các ứng dụng mật mã học như mã hóa, chữ ký số, v.v.
Tác giả: Vitalik Buterin
Ngày đăng: 14 tháng 1 năm 2017
Một trong những mô hình nền tảng chính đằng sau nhiều cơ sở hạ tầng mật mã học như "chữ ký ngưỡng xác định" (deterministic threshold signature), zk-SNARKs và các dạng chứng minh không kiến thức đơn giản hơn khác là phép ghép cặp đường cong elliptic. Các đường cong elliptic đã được sử dụng rộng rãi trong các ứng dụng mật mã học như mã hóa và chữ ký số trong hơn ba thập kỷ qua, còn "phép ghép cặp đường cong elliptic" (EC pairings) hay ánh xạ song tuyến tính là một phát triển mới gần đây dựa trên đó, mang đến phép nhân mật mã học, từ đó mở rộng đáng kể khả năng của các giao thức dựa trên đường cong elliptic. Bài viết này sẽ trình bày chi tiết về phép ghép cặp đường cong elliptic và giải thích sơ lược cách nó hoạt động.
Do khái niệm này thực sự rất khó hiểu, bạn đừng mong đọc một lần rồi hiểu ngay – dù có thể phải đọc đến lần thứ mười đi nữa – nhưng hy vọng bài viết này sẽ giúp bạn phần nào thấu hiểu được bí ẩn đằng sau nó.
Bản thân đường cong elliptic đã là một chủ đề khá khó nắm bắt, tuy nhiên bài viết này thường xuyên giả định rằng bạn đã có một số hiểu biết nhất định về cách chúng hoạt động; nếu chưa, tôi khuyên bạn nên đọc bài viết này để làm quen trước.
Tóm lại, đường cong elliptic xử lý các đối tượng toán học gọi là "điểm (points)", cụ thể là các điểm hai chiều (x, y) trên mặt phẳng, cùng với các công thức đặc biệt cho các phép cộng và trừ (ví dụ R = P + Q), và bạn cũng có thể nhân một điểm với một số nguyên (ví dụ P * n = P + P + ... + P, mặc dù khi n lớn thì có một thuật toán nhanh hơn nhiều).
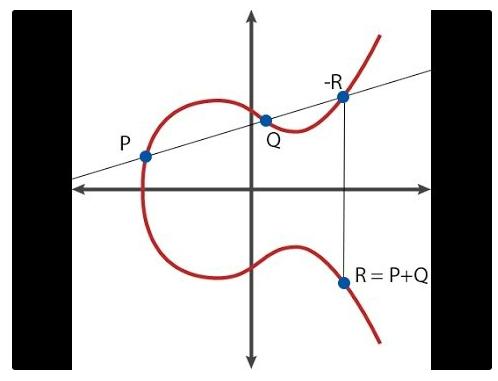
Đây là hình ảnh minh họa cho phép cộng điểm
Ngoài ra còn có một điểm đặc biệt gọi là "điểm vô cực" (O), đóng vai trò phần tử trung tính trong các phép toán điểm, nghĩa là với mọi điểm P đều có P + O = P. Một đường cong còn có một thuộc tính gọi là "bậc (order)", tức là tồn tại một số nguyên dương n sao cho với mọi P ta có P * n = O (và do đó P * (n + 1) = P, P * ((7*n) + 5) = P * 5, v.v.). Ngoài ra còn có một "điểm sinh (generator point)" G được thỏa thuận trước, đóng vai trò như phần tử đơn vị đại diện cho số 1. Về lý thuyết, bất kỳ điểm nào trên đường cong cũng có thể làm điểm sinh, điều quan trọng là G phải được chọn thống nhất.
Phép ghép cặp cho phép bạn kiểm tra một lớp đẳng thức phức tạp hơn: ví dụ, nếu P = G * p, Q = G * q, R = G * r, bạn muốn kiểm tra xem p * q = r có đúng hay không, thì chỉ cần tọa độ của ba điểm P, Q, R làm đầu vào là đủ. Điều này có vẻ như phá vỡ đảm bảo an toàn cơ bản nhất của đường cong elliptic, vì dường như biết tọa độ điểm P sẽ làm rò rỉ giá trị p. Nhưng thực tế thì nguy cơ rò rỉ này bị giới hạn nghiêm trọng — cụ thể, giả thiết Diffie-Hellman phân biệt là dễ giải, nhưng phiên bản tính toán vẫn "không khả thi về mặt tính toán". Nói cách khác, độ khó ít nhất cũng tương đương với việc không biết giá trị đó.
Cách thứ ba để hiểu "phép ghép cặp", có lẽ là cách trực quan nhất trong hầu hết các ngữ cảnh sử dụng mà chúng ta đang thảo luận, là nếu coi các điểm trên đường cong elliptic như một hàm mật mã một chiều (tức là encrypt(p) = p * G = P), thì trong khi toán học đường cong elliptic truyền thống cho phép kiểm tra các ràng buộc tuyến tính giữa các biến (ví dụ P = G * p, Q = G * q, R = G * r, kiểm tra 5 * P + 7 * Q = 11 * R đồng nghĩa với kiểm tra 5 * p + 7 * q = 11 * r), thì phép ghép cặp đường cong elliptic cho phép kiểm tra các ràng buộc bậc hai (kiểm tra e(P, Q) * e(G, G * 5) = 1 đồng nghĩa với kiểm tra p * q + 5 = 0). Chỉ cần có khả năng xử lý bậc hai là đủ để thực hiện các ứng dụng thú vị như chữ ký ngưỡng xác định, QAP (chương trình số học bậc hai - quadratic arithmetic programs, một dạng chứng minh không kiến thức), v.v.
Vấn đề hiện tại là toán tử e(P, Q) mà chúng ta vừa giới thiệu ở trên thực chất là gì? Đây chính là một "phép ghép cặp". Các nhà toán học đôi khi gọi nó là "ánh xạ song tuyến tính", và "song tuyến tính" ở đây cơ bản có nghĩa là nó thỏa mãn các điều kiện sau:
e(P, Q + R) = e(P, Q) * e(P, R)
e(P + S, Q) = e(P, Q) * e(S, Q)
Lưu ý rằng ở đây dấu + và * có thể là các toán tử tùy ý; khi xây dựng một loại đối tượng toán học mới, đại số trừu tượng không quan tâm đến việc + và * được "định nghĩa" như thế nào, miễn là chúng tuân theo các quy tắc quen thuộc như a + b = b + a, (a * b) * c = a * (b * c), (a * c) + (b * c) = (a + b) * c.
Giả sử bây giờ P, Q, R, S chỉ là các con số, thì hàm ghép cặp rất dễ xây dựng: ta có thể định nghĩa e(x, y) = 2^(xy). Khi đó ta thấy:
e(3, 4 + 5) = 2^(3 * 9) = 2²⁷
e(3, 4) * e(3, 5) = 2^(3 * 4) * 2^(3 * 5) = 2¹² * 2¹⁵ = 2²⁷
Thật vậy, nó là song tuyến tính!
Tuy nhiên, phép ghép cặp đơn giản như vậy lại không phù hợp để dùng trong mật mã học, vì việc phân tích các đối tượng toán học chỉ hoạt động trên các số nguyên là quá dễ dàng; các tính chất của số nguyên khiến các thao tác như chia, logarit trở nên dễ dàng. Số nguyên cũng không có khái niệm "khóa công khai" hay "hàm một chiều". Hơn nữa, phép ghép cặp như mô tả ở trên là có thể đảo ngược: biết x và biết e(x, y), bạn có thể tính ra y bằng cách chia và lấy logarit. Chúng ta muốn một cấu trúc toán học càng giống "hộp đen" càng tốt: bạn chỉ có thể thực hiện một vài phép cộng, trừ, nhân, chia, và chỉ có vậy. Đây là lúc mà đường cong elliptic và phép ghép cặp đường cong elliptic phát huy tác dụng.
Người ta đã phát hiện ra rằng thực sự có thể xây dựng ánh xạ song tuyến tính trên các điểm của đường cong elliptic — nghĩa là khi đầu vào là hai điểm P và Q trên đường cong elliptic, xây dựng một hàm e(P, Q) ánh xạ tới một phần tử của F_p¹² (ít nhất là trong trường hợp cụ thể này là đủ dùng, và chi tiết này phụ thuộc vào đường cong, sẽ nói thêm sau), nhưng toán học đằng sau việc thực hiện điều này thực sự rất phức tạp.
Trước tiên, ta hãy tìm hiểu về các trường số nguyên tố (prime fields) và các trường mở rộng (extension fields). Dù đường cong trong hình vẽ trông đẹp mắt, nhưng nó chỉ có dạng như vậy khi ta giả sử phương trình định nghĩa đường cong được đặt trên tập số thực thông thường. Nếu thực sự dùng số thực trong mật mã học, bạn có thể dùng logarit để "đảo ngược", khiến mọi thứ mất tác dụng, chưa kể việc lưu trữ số thực có thể đòi hỏi không gian vô hạn. Do đó, thay vào đó ta dùng các con số trên trường hữu hạn.
Một trường số nguyên tố gồm tập hợp các số 0, 1, 2, ..., (p−1), trong đó p là một số nguyên tố, và các phép toán được định nghĩa như sau:
a + b: (a + b) % p
a * b: (a * b) % p
a - b: (a - b) % p
a / b: (a * b^(p-2)) % p
Về cơ bản, tất cả các phép toán đều được thực hiện theo modulo p (có phần giới thiệu về modulo tại đây). Phép chia là một trường hợp đặc biệt. Thông thường, 3/2 không phải là số nguyên, nhưng chúng ta muốn chỉ xử lý các số nguyên, nên thay vào đó ta tìm số nguyên x sao cho x * 2 = 3, với * là phép nhân modulo như đã định nghĩa ở trên. May mắn thay, nhờ định lý nhỏ Fermat, định nghĩa mũ cho phép chia này đáp ứng được yêu cầu, nhưng còn có một cách nhanh hơn là dùng thuật toán Euclid mở rộng. Giả sử p = 7, dưới đây là một vài ví dụ:
2 + 3 = 5 % 7 = 5
4 + 6 = 10 % 7 = 3
2 - 5 = -3 % 7 = 4
6 * 3 = 18 % 7 = 4
3 / 2 = (3 * 2^5) % 7 = 5
5 * 2 = 10 % 7 = 3
Nếu bạn thử thao tác với các phép toán như vậy, bạn sẽ thấy chúng nhất quán và tuân theo mọi quy tắc thông thường. Hai ví dụ cuối cho thấy (a / b) * b = a, bạn cũng có thể thấy (a + b) + c = a + (b + c), (a + b) * c = a * c + b * c, và các đẳng thức đại số khác mà bạn từng biết và yêu thích ở phổ thông vẫn tiếp tục hoạt động. Trong thực tế, các đường cong elliptic được sử dụng thường hoạt động trên các trường số nguyên tố.
Bây giờ ta nói đến các trường mở rộng. Bạn có thể đã gặp các trường mở rộng trước đây; ví dụ điển hình nhất trong sách giáo khoa toán học là trường số phức — được tạo thành bằng cách mở rộng trường số thực với phần tử mới sqrt(-1) = i. Nói đơn giản, một trường mở rộng là việc "sáng tạo" một phần tử mới trên một trường sẵn có, và định nghĩa mối quan hệ giữa phần tử mới này và các phần tử hiện tại (trong ví dụ trên là i² + 1 = 0); mối quan hệ này không được thỏa mãn bởi bất kỳ số nào hiện có, và tập hợp kết quả là tập hợp tất cả các tổ hợp tuyến tính (linear combination) của các phần tử cũ với phần tử mới.
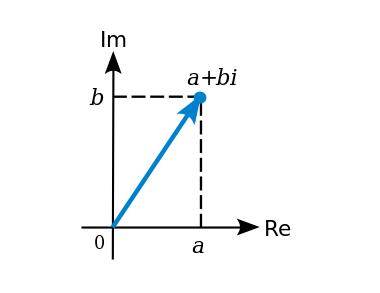
Chúng ta cũng có thể mở rộng các trường số nguyên tố; ví dụ, thêm i như trên vào trường số nguyên tố mod 7, ta có:
(2 + 3i) + (4 + 2i) = 6 + 5i
(5 + 2i) + 3 = 1 + 2i
(6 + 2i) * 2 = 5 + 4i
4i * (2 + i) = 3 + i
Phép cuối có thể khó hiểu hơn; bước đầu tiên là phân phối phép nhân bên trái thành 4i * 2 + 4i * i, thu được 8i - 4. Vì ta đang làm việc trong modulo 7, số này trở thành i + 3. Với phép chia:
a / b : (a * b^(p^2-2)) % p
Ở đây, số mũ trong định lý Fermat nhỏ tăng từ p lên p², tất nhiên cũng có thể dùng thuật toán Euclid mở rộng để tính hiệu quả hơn. Vì với mọi phần tử x trong trường ta đều có x^(p² − 1) = 1, nên ta gọi (p² − 1) là "bậc của nhóm nhân trong trường".
Đối với trường số thực, định lý cơ bản đại số đảm bảo rằng mở rộng bậc hai (quadratic extension) của nó — trường số phức — là đóng đại số (lưu ý người dịch: đúng ra phải là đóng đại số, chứ không phải đầy đủ; trường số thực cũng đầy đủ nhưng vẫn mở rộng được) — tức là trường này không thể mở rộng thêm, vì mọi phần tử mới j và mối quan hệ toán học cần thỏa mãn với các số phức hiện tại (về mặt kỹ thuật là các quan hệ đa thức) đều đã có phần tử trong trường thỏa mãn. Nhưng với các trường số nguyên tố thì không có vấn đề này, ta có thể mở rộng bậc ba (cubic extension) (phần tử mới w thỏa mãn một đa thức bậc ba, do đó 1, w, w² độc lập tuyến tính), bậc cao hơn, hoặc thậm chí mở rộng liên tiếp nhiều lần. Các đường cong elliptic được xây dựng trên các "số phức modulo" này.
Nếu bạn quan tâm đến việc hiện thực hóa các toán học này thành mã nguồn, đây là một vài ví dụ hiện thực các trường số nguyên tố và trường mở rộng.
Quay lại phép ghép cặp đường cong elliptic. Phép ghép cặp đường cong elliptic (loại mà chúng ta đang thảo luận chỉ là một dạng, nhưng logic là tương tự) là một ánh xạ G2 × G1 → Gt, trong đó:
- G1 là một đường cong elliptic, các điểm trên đó thỏa mãn phương trình dạng y² = x³ + b, và tọa độ x, y của các điểm là các phần tử của F_p (nghĩa là chúng chỉ là các số thông thường, nhưng các phép tính số học được thực hiện theo modulo một số nguyên tố).
- G2 cũng là một đường cong elliptic, thỏa mãn cùng phương trình như G1, nhưng tọa độ x, y của các phần tử trong G2 là các phần tử của F_p¹² (đây là các "số phức" mà ta vừa nói; ta định nghĩa một số kỳ diệu w thỏa mãn đa thức bậc 12: w¹² − 18w⁶ + 82 = 0).
- Gt là tập hợp kết quả của các phép toán trên đường cong elliptic. Trong đường cong chúng ta đang xét, Gt là F_p¹² (cùng loại "số phức" như dùng cho G2).
Tính chất chính cần thỏa mãn là tính song tuyến tính, trong ngữ cảnh này có nghĩa là:
e(P, Q + R) = e(P, Q) * e(P, R)
e(P + Q, R) = e(P, R) * e(Q, R)
(lưu ý người dịch: chính xác hơn đây là "song tuyến tính trên ℤ", chỉ vì các điểm trên đường cong elliptic đang xét đều là các điểm nguyên, và phép nhân, cộng được định nghĩa là thực hiện trên số nguyên rồi lấy modulo, nên tự nhiên thỏa mãn một số tính chất tuyến tính)
Việc chọn hàm ghép cặp còn phải tuân theo hai tiêu chí quan trọng:
- Tính toán phải đủ hiệu quả (ví dụ, ta có thể trực tiếp lấy logarit rời rạc của mọi điểm rồi nhân chúng lại, như một phương pháp ghép cặp đơn giản, nhưng chi phí tính toán này khó ngang với việc phá mật mã đường cong elliptic, nên không chấp nhận được).
- Không suy biến (bạn hoàn toàn có thể định nghĩa e(P, Q) = 1, nhưng đó không phải là một phép ghép cặp hữu ích).
Vậy làm thế nào để đạt được điều này?
Toán học đằng sau việc vận hành hàm ghép cặp rất khó và đòi hỏi đại số nâng cao vượt xa những gì chúng ta đã thấy đến nay, nhưng tôi sẽ phác họa sơ lược. Trước tiên, ta cần định nghĩa khái niệm "ước (divisor)", về cơ bản là một cách biểu diễn khác cho các hàm số tác động lên các điểm trên đường cong elliptic. Ước của một hàm cơ bản tính toán số lượng điểm không và điểm tiến đến vô cùng của hàm đó. Để hiểu rõ hơn, hãy xem một vài ví dụ. Chọn một điểm P = (P_x, P_y), rồi xét hàm số:
f(x, y) = x − P_x
Ước của nó là [P] + [−P] − 2 * [O] (các dấu ngoặc vuông ở đây biểu thị điểm xuất hiện trong tập hợp các điểm không và điểm tiến đến vô cùng của hàm, chứ không phải bản thân điểm đó; [P] + [Q] khác với [P + Q]). Lý do như sau:
- Hàm này bằng 0 tại điểm P, vì x = P_x nên x − P_x = 0.
- Hàm này bằng 0 tại điểm −P, vì −P và P có cùng tọa độ x.
- Khi x tiến đến vô cùng, hàm này cũng tiến đến vô cùng, nên ta nói hàm tiến đến vô cùng tại điểm O. Điểm vô cực này được tính hai lần, nên O nhân với hệ số -2 (dấu âm vì nó là điểm vô cực, khác với điểm không; hệ số 2 vì nó được tính hai lần).
Lý do tính toán đại khái là: vì phương trình đường cong là x³ = y² + b, khi x tăng, để y² đạt quy mô tương đương, tốc độ tăng của y cần khoảng 1.5 lần x. Do đó, nếu một hàm tuyến tính chỉ chứa x, hệ số vô cực là 2, nhưng nếu chứa y thì hệ số là 3.
Bây giờ xét hàm của một đường thẳng:
ax + by + c = 0
với a, b, c được chọn sao cho đường thẳng đi qua điểm P và Q. Theo cách hoạt động của phép cộng đường cong elliptic, nó cũng sẽ đi qua điểm −P−Q. Vì khi tiến đến vô cùng, nó phụ thuộc vào cả x và y, nên ước là [P] + [Q] + [−P−Q] − 3 * [O].
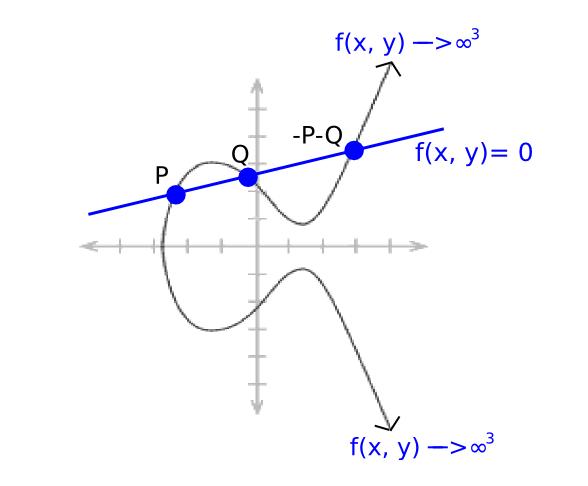
Ta biết rằng mọi "hàm hữu tỷ" (tức là các hàm được định nghĩa bằng các phép cộng, trừ, nhân, chia hữu hạn trên tọa độ điểm) tương ứng duy nhất với một ước, sai khác một hằng số (nghĩa là nếu hai hàm F và G có cùng ước, thì tồn tại hằng số k sao cho F = G * k).
Với mọi hai hàm F và G, ước của (F * G) bằng tổng ước của F và G (trong sách toán học ta thấy (F * G) = (F) + (G)), ví dụ f(x, y) = P_x − x, thì (f³) = 3 * [P] + 3 * [−P] − 6 * [O]; P và −P được tính ba lần vì theo một nghĩa toán học đặc biệt nào đó, f³ tiến đến 0 "gấp ba lần" nhanh hơn.
Lưu ý một định lý nói rằng nếu bạn bỏ dấu ngoặc vuông trong một ước và thực hiện phép toán trên các điểm, kết quả luôn là O ([P] + [Q] + [−P−Q] − 3 * [O] cho ra P + Q − P − Q − 3 * O = O), và mọi ước có tính chất này đều là ước của một hàm nào đó.
Bây giờ ta có thể bắt đầu xem xét phép ghép cặp Tate. Xét các hàm được định nghĩa bằng ước sau:
- (F_P) = n * [P] − n * [O], với n là bậc của G1, tức là với mọi P, n * P = O
- (F_Q) = n * [Q] − n * [O]
- (g) = [P + Q] − [P] − [Q] + [O]
Bây giờ, hãy xem tích F_P * F_Q * g^n. Ước của nó là:
n * [P] − n * [O] + n * [Q] − n * [O] + n * [P + Q] − n * [P] − n * [Q] + n * [O]
Rút gọn ta được:
n * [P + Q] − n * [O]
Lưu ý rằng dạng ước này khớp với dạng ước của F_P và F_Q. Do đó, F_P * F_Q * g^n = F_(P + Q).
Bây giờ thêm một bước gọi là "lũy thừa cuối cùng (final exponentiation)", nâng kết quả của các phép toán trước (F_P, F_Q, v.v.) lên lũy thừa z = (p¹² − 1) / n, trong đó p¹² − 1 là bậc của nhóm nhân trong F_p¹² (nói cách khác, với mọi x ∈ F_p¹², x^(p¹² − 1) = 1). Lưu ý rằng nếu bạn áp dụng số mũ này lên bất kỳ kết quả nào đã là lũy thừa bậc n, bạn sẽ thu được lũy thừa bậc (p¹² − 1) của một phần tử, kết quả là 1. Do đó, sau bước lũy thừa cuối cùng, g^n sẽ bị triệt tiêu, và ta có F_P^z * F_Q^z = F_(P + Q)^z. Như vậy, ta có được một phần của tính song tuyến tính.
Bây giờ, nếu bạn muốn xây dựng một hàm song tuyến tính trên cả hai tham số, bạn cần toán học phức tạp hơn, không chỉ tính F_P mà còn phải tính ước của F_P, và tiếp tục sẽ dẫn đến phép ghép cặp Tate hoàn chỉnh. Để chứng minh thêm, bạn cần hiểu các khái niệm như "tương đương tuyến tính (linear equivalence)" và luật Weil. Chi tiết về các khái niệm này có thể xem tại đây và tại đây.
Ở đây đã hiện thực một biến thể sửa đổi của phép ghép cặp Tate — Optimal Ate Pairing. Mã nguồn này cũng hiện thực việc tính F_p bằng thuật toán Miller.
Thực tế, việc sử dụng phép ghép cặp này giống như rút ra một thanh kiếm hai lưỡi: một mặt, nó cho phép chúng ta thực hiện các giao thức khác nhau; mặt khác, nó cũng đòi hỏi chúng ta phải hết sức cẩn thận khi lựa chọn đường cong elliptic.
Mỗi đường cong elliptic đều có một giá trị gọi là bậc nhúng (embedding degree) — số nguyên nhỏ nhất k sao cho p^k − 1 là bội của n (p là số nguyên tố dùng cho trường, n là bậc của đường cong). Trong trường đã đề cập ở trên, k = 12; trong mật mã học đường cong elliptic truyền thống (khi không quan tâm đến phép ghép cặp), các trường thường có bậc nhúng rất lớn, khiến việc tính toán phép ghép cặp là không khả thi về mặt tính toán. Tuy nhiên, nếu không cẩn thận, ta có thể vô tình xây dựng các trường có k = 4 hoặc thậm chí k = 1.
Khi k = 1, "vấn đề logarit rời rạc" trên đường cong elliptic (tính p khi chỉ biết điểm P = G * p — tức là vấn đề bạn cần giải để "phá" khóa riêng của đường cong elliptic) có thể bị rút gọn thành một vấn đề tương đối đơn giản trên F_p (phương pháp này gọi là tấn công MOV); việc sử dụng một đường cong elliptic có bậc nhúng lớn hơn hoặc bằng 12 sẽ đảm bảo rằng sự rút gọn này là không khả thi, hoặc vấn đề rút gọn ra ít nhất cũng khó như việc tính khóa riêng từ khóa công khai bằng phương pháp "bình thường". Hiện nay, tất cả các tham số đường cong chuẩn đều đã được kiểm tra kỹ lưỡng để tránh vấn đề này.
Chào mừng tham gia cộng đồng chính thức TechFlow
Nhóm Telegram:https://t.me/TechFlowDaily
Tài khoản Twitter chính thức:https://x.com/TechFlowPost
Tài khoản Twitter tiếng Anh:https://x.com/BlockFlow_News
















