Tìm hiểu giao thức cam kết đa thức Brakedown trong FOAKS qua một bài viết
Tuyển chọn TechFlowTuyển chọn TechFlow
Tìm hiểu giao thức cam kết đa thức Brakedown trong FOAKS qua một bài viết
Nếu các nhà mật mã học không phát hiện ra mối liên hệ giữa tích ten-xơ (Tensor Product) và giá trị đa thức, thì sẽ rất khó xuất hiện giao thức cam kết đa thức Brakedown, từ đó cũng không thể có Orion dựa trên Brakedown hay FOAK.
Tác giả: Khang Thủy Việt, CEO Fox Tech; Mạnh Huyền Tế, Nhà khoa học trưởng Fox Tech
Lời mở đầu: Nếu các nhà mật mã học không phát hiện ra mối liên hệ giữa tích tenxơ (Tensor Product) và việc đánh giá đa thức, thì sẽ rất khó xuất hiện giao thức cam kết đa thức Brakedown, từ đó cũng không thể có những thuật toán mới nhanh chóng như Orion hay FOAKS dựa trên Brakedown.
Trong nhiều hệ thống chứng minh kiến thức không tiết lộ (zero-knowledge proof) phụ thuộc vào cam kết đa thức, người ta sử dụng các giao thức cam kết khác nhau. Theo đánh giá của Justin Thaler từ a16z trong bài viết tháng 8 năm 2022 có tựa đề “Measuring SNARK performance: Frontends, backends, and the future”, mặc dù Brakedown có kích thước bằng chứng (Proof Size) khá lớn, nhưng rõ ràng đây là giao thức cam kết đa thức nhanh nhất hiện nay.
FRI, KZG, Bulletproof là những giao thức cam kết đa thức phổ biến hơn, tuy nhiên tốc độ lại là điểm nghẽn của chúng. Các thuật toán như Plonky do zkSync sử dụng, Plonky 2 do Polygon zkEVM sử dụng, Ultra-Plonk do Scroll sử dụng đều là những giao thức cam kết đa thức dựa trên KZG. Bên chứng minh (Prover) phải thực hiện lượng lớn phép tính FFT và MSM để sinh đa thức và cam kết, cả hai thao tác này đều tạo gánh nặng tính toán lớn. Dù MSM có tiềm năng tăng tốc bằng đa luồng, nhưng cần bộ nhớ lớn và ngay cả với mức độ song song cao vẫn chậm, trong khi FFT quy mô lớn lại phụ thuộc nghiêm trọng vào việc thường xuyên xáo trộn dữ liệu trong quá trình chạy thuật toán, khiến khó tăng tốc phân tán qua cụm máy tính.
Chính nhờ có giao thức cam kết đa thức nhanh hơn Brakedown mà độ phức tạp tính toán của các thao tác này được giảm đáng kể.
FOAKS, viết tắt của Fast Objective Argument of Knowledges, là một khuôn khổ hệ thống chứng minh kiến thức không tiết lộ do Fox Tech đề xuất, dựa trên Brakedown. FOAKS tiếp tục giảm thiểu phép tính FFT so với Orion, với mục tiêu cuối cùng là loại bỏ hoàn toàn FFT. Ngoài ra, FOAKS còn thiết kế một phương pháp đệ quy chứng minh hoàn toàn mới và tinh tế nhằm giảm kích thước bằng chứng. Ưu điểm của khuôn khổ FOAKS là đạt được thời gian chứng minh tuyến tính đồng thời giữ kích thước bằng chứng nhỏ, rất phù hợp để ứng dụng trong các kịch bản zkRollup.
Dưới đây chúng tôi sẽ trình bày chi tiết về giao thức cam kết đa thức Brakedown được sử dụng trong FOAKS.
Trong lĩnh vực mật mã học, giao thức cam kết (Commitment) là bên chứng minh (Prover) cam kết một giá trị bí mật, sinh ra một giá trị công khai, giá trị này phải đảm bảo tính ràng buộc (Binding) và tính ẩn danh (Hiding). Sau đó, bên gửi cam kết mở cam kết này và gửi thông điệp cho bên kiểm tra để xác minh mối quan hệ tương ứng giữa cam kết và thông điệp. Điều này khiến giao thức cam kết có nhiều điểm chung với hàm băm, nhưng giao thức cam kết thường dựa vào các cấu trúc toán học trong lĩnh vực mật mã khóa công khai. Cam kết đa thức (Polynomial Commitment) là một dạng giao thức cam kết đối với đa thức, tức là giá trị được cam kết là một đa thức. Đồng thời, giao thức cam kết đa thức còn bao gồm thuật toán đánh giá tại một điểm đã cho và đưa ra bằng chứng, làm cho cam kết đa thức trở thành một lớp giao thức mật mã quan trọng, là phần cốt lõi của nhiều hệ thống chứng minh kiến thức không tiết lộ.
Trong nghiên cứu gần đây về mật mã học, nhờ phát hiện ra mối liên hệ giữa tích tenxơ (Tensor Product) và việc đánh giá đa thức nên đã xuất hiện loạt giao thức cam kết đa thức liên quan, Brakedown là đại diện tiêu biểu.
Trước khi đi sâu vào chi tiết giao thức Brakedown, cần nắm vững một số kiến thức cơ bản. Chúng ta cần hiểu về mã tuyến tính (Linear Code), hàm băm kháng va chạm (Hash Function), cây Merkle (Merkle Tree), phép toán tích tenxơ (Tensor Product), và biểu diễn tích tenxơ của việc đánh giá đa thức.
Đầu tiên là mã tuyến tính (Linear Code). Một mã tuyến tính với độ dài tin nhắn k và độ dài mã là n là một không gian con tuyến tính C ⊂ F^n, sao cho tồn tại một ánh xạ đơn ánh từ tin nhắn đến mã, gọi là mã hóa, ký hiệu EC: F^k → C. Bất kỳ tổ hợp tuyến tính nào của các từ mã cũng vẫn là một từ mã. Khoảng cách giữa hai từ mã u, v chính là khoảng cách Hamming của chúng, ký hiệu Δ(u, v).
Khoảng cách ngắn nhất là d = min_{u,v} Δ(u, v). Mã như vậy được ký hiệu là [n, k, d] mã tuyến tính, dùng d/n để biểu thị khoảng cách tương đối của mã.
Tiếp theo là hàm băm kháng va chạm (Hash Function) và cây Merkle (Merkle Tree).
Sử dụng H: {0, 1}^{2λ} → {0, 1}^λ để biểu thị một hàm băm. Cây Merkle là một cấu trúc dữ liệu đặc biệt, cho phép cam kết 2^d tin nhắn và sinh ra một giá trị băm h, khi mở bất kỳ tin nhắn nào cần cung cấp d+1 giá trị băm.
Cây Merkle có thể được biểu diễn dưới dạng cây nhị phân có độ sâu d, trong đó L phần tử tin nhắn m₁, m₂, ..., mₗ lần lượt tương ứng với các lá của cây. Mỗi nút nội bộ của cây được tính bằng cách băm hai nút con của nó. Khi mở tin nhắn mᵢ, cần tiết lộ đường đi từ mᵢ đến nút gốc.
Sử dụng các ký hiệu sau để biểu diễn:
-
h ← Merkle.Commit(m₁, ..., mₗ)
-
(mᵢ, πᵢ) ← Merkle.Open(m, i)
-
{0, 1} ← Merkle.Verify(πᵢ, mᵢ, h)
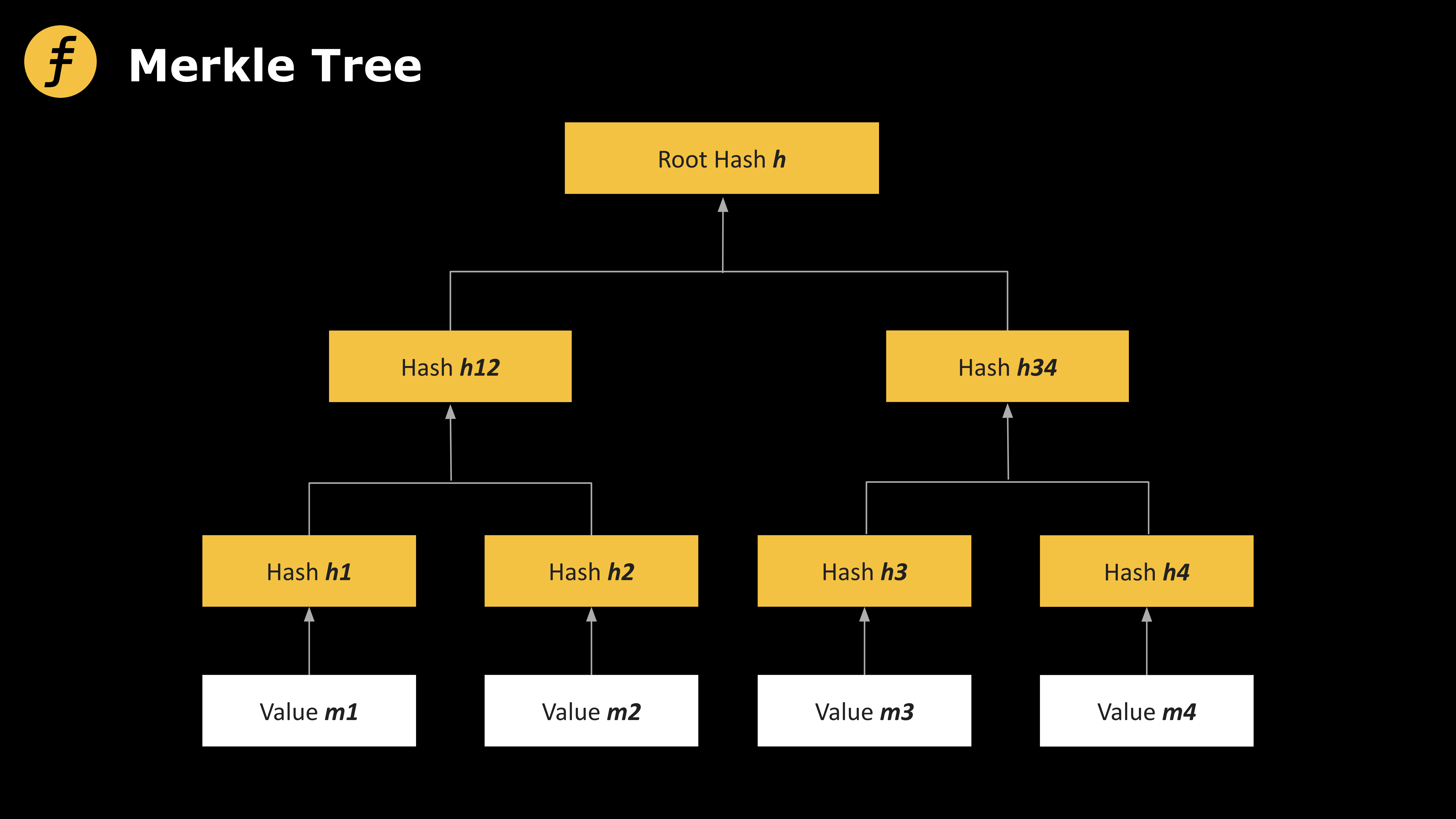
Hình 1: Cây Merkle (Merkle Tree)
Chúng ta cũng cần hiểu cách thực hiện phép toán tích tenxơ (Tensor Product). Về mặt toán học, tenxơ là sự mở rộng của vectơ và ma trận sang không gian chiều cao, là đối tượng nghiên cứu quan trọng; thảo luận chi tiết về tenxơ vượt quá phạm vi bài viết này, ở đây chỉ giới thiệu phép toán tích tenxơ của vectơ và ma trận.
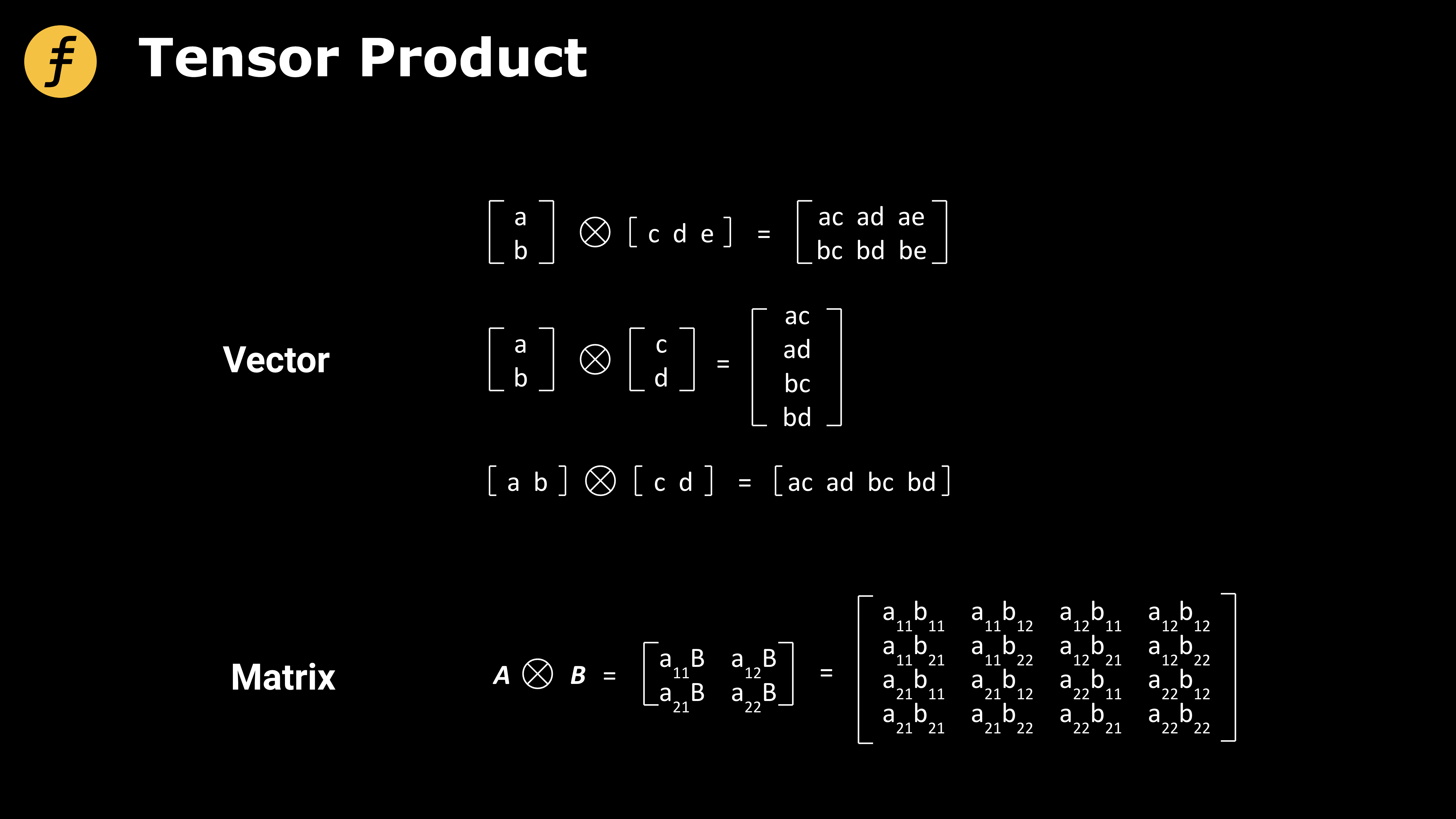
Hình 2: Phép toán tích tenxơ của vectơ và ma trận
Tiếp theo, chúng ta cần biết biểu diễn tích tenxơ của việc đánh giá đa thức.
[GLS+] đề cập rằng việc đánh giá đa thức có thể được biểu diễn dưới dạng tích tenxơ. Trong trường hợp này, chúng ta xét cam kết đa thức đa tuyến tính.
Cụ thể hơn, cho trước một đa thức, giá trị của nó tại vectơ x₀, x₁, ..., x_{logN-1} có thể viết thành:
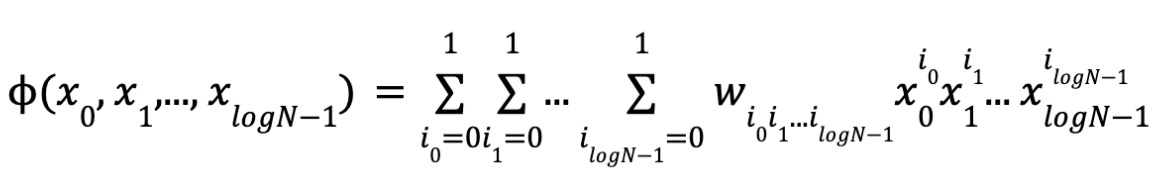
Theo định nghĩa đa tuyến tính, bậc của mỗi biến là 0 hoặc 1, do đó ở đây có N hạng tử đơn và hệ số, cùng logN biến. Đặt
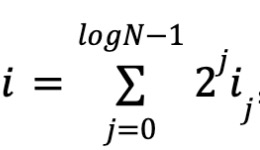
trong đó i₀i₁...i_{logN-1} là biểu diễn nhị phân của i. Gọi w là hệ số đa thức,
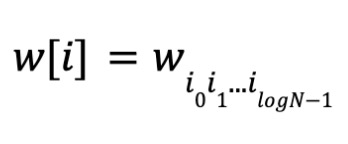
Tương tự, định nghĩa
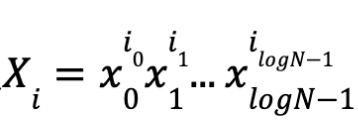
Đặt
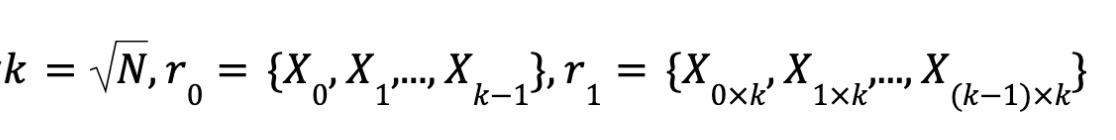
Do đó có X = r₀ ⊗ r₁.
Như vậy, việc đánh giá đa thức có thể được biểu diễn dưới dạng tích tenxơ: ϕ(x₀, x₁, ..., x_{logN-1}) = ⟨w, r₀ ⊗ r₁⟩.
Cuối cùng, chúng ta xem xét quy trình Brakedown được sử dụng trong FOAKS, Orion [XZS 22].
Đầu tiên, PC.Commit chia hệ số đa thức w thành dạng ma trận k×k, rồi mã hóa nó (tham khảo mã tuyến tính trong "Kiến thức chuẩn bị"), ký hiệu là C₂. Sau đó, xây dựng một cây Merkle cho từng cột C₂[:, i], rồi xây dựng thêm một cây Merkle nữa trên các gốc cây Merkle của từng cột, làm cam kết cuối cùng.
Trong quá trình chứng minh giá trị, cần chứng minh hai điểm: tính gần đúng (Proximity) và tính nhất quán (Consistency). Tính gần đúng đảm bảo ma trận cam kết thực sự đủ gần với một từ mã sau khi mã hóa. Tính nhất quán đảm bảo y = ⟨w, r₀ ⊗ r₁⟩.
Kiểm tra tính gần đúng: Kiểm tra tính gần đúng gồm hai bước. Trước tiên, bên kiểm tra gửi một vectơ ngẫu nhiên Y₀ cho bên chứng minh, bên chứng minh tính tích vô hướng Y₀ với C₁, tức là tính tổ hợp tuyến tính các hàng của C₁ với các thành phần của Y₀ làm hệ số. Do tính chất của mã tuyến tính, C_{Y₀} là từ mã của Y_{y₀}. Sau đó, bên chứng minh chứng minh rằng C_{Y₀} thực sự được tính từ từ mã đã cam kết. Để chứng minh điều này, bên kiểm tra chọn ngẫu nhiên t cột, bên chứng minh mở các cột tương ứng và cung cấp bằng chứng cây Merkle. Bên kiểm tra kiểm tra xem tích vô hướng của các cột và Y₀ có bằng các vị trí tương ứng trong C_{Y₀} hay không. [BCG 20] chứng minh rằng nếu mã tuyến tính sử dụng có khoảng cách tương đối là hằng số, thì ma trận đã cam kết gần với một từ mã với xác suất áp đảo (xác suất phủ định mệnh đề là có thể bỏ qua).
Kiểm tra tính nhất quán: Quy trình kiểm tra tính nhất quán giống hệt với kiểm tra tính gần đúng. Điểm khác biệt là không dùng vectơ ngẫu nhiên Y₀ mà dùng trực tiếp r₀ để thực hiện phần tổ hợp tuyến tính. Tương tự, c₁ cũng là mã tuyến tính của tin nhắn y₁, và có ϕ(x) = ⟨y₁, r₁⟩. [BCG 20] chứng minh rằng, qua kiểm tra tính nhất quán, nếu ma trận đã cam kết gần với một từ mã, thì với xác suất áp đảo, y = ϕ(x).
Dưới dạng mã giả, ta trình bày quy trình giao thức Brakedown:
Đầu vào công khai: Điểm đánh giá X, được phân tích thành tích tenxơ X = r₀ ⊗ r₁;
Đầu vào riêng tư: Đa thức ϕ, hệ số ký hiệu là w.
Gọi C là mã tuyến tính [n, k, d], EC: F^k → F^n là hàm mã hóa, N = k×k. Nếu N không phải số chính phương, có thể thêm dữ liệu để làm tròn lên số chính phương gần nhất. Sử dụng ký hiệu kiểu Python mat[:, i] để chọn cột thứ i của ma trận mat.
-
function PC.Commit(ϕ):
-
Phân tích w thành ma trận k×k. Bên chứng minh tính cục bộ mã hóa mã tenxơ C₁, C₂, trong đó C₁ là ma trận k×n, C₂ là ma trận n×n.
-
for i ∈ [n] do
-
Tính gốc cây Merkle Rootᵢ = Merkle.Commit(C₂[:, i])
-
Tính gốc cây Merkle R = Merkle.Commit([Root₀, ..., Root_{n-1}]), và xuất R làm cam kết.
-
function PC.Prover(ϕ, X, R)
-
Bên chứng minh nhận được vectơ ngẫu nhiên Y₀ ∈ F^k từ bên kiểm tra
-
Tính gần đúng
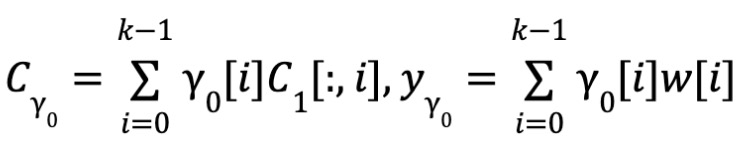
-
Tính nhất quán
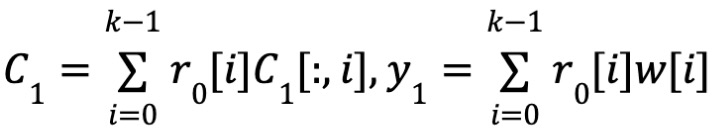
-
Bên chứng minh gửi C₁, y₁, C₀, y₀ cho bên kiểm tra.
-
Bên kiểm tra chọn ngẫu nhiên mảng t[n] ký hiệu Î và gửi cho bên chứng minh
-
for idx ∈ Î do
-
Bên chứng minh gửi C₁[:, idx] và bằng chứng cây Merkle của Root_idx cho C₂[:, idx] dưới R tới bên kiểm tra
-
function PC.VERIFY_EVAL(π_X, X, y=ϕ(X), R)
-
Tính gần đúng: ∀idx ∈ Î, C_{Y₀}[idx] == ⟨Y₀, C₁[:, idx]⟩ và EC(Y_{y₀}) == C_{Y₀}
-
Tính nhất quán: ∀idx ∈ Î, C₁[idx] == ⟨Y₀, C₁[:, idx]⟩ và EC(Y₁) == C₁
-
y == ⟨r₁, y₁⟩
-
∀idx ∈ Î, EC(C₁[:, idx]) phù hợp với ROOT_idx, và bằng chứng cây Merkle của ROOT_idx hợp lệ.
-
Xuất chấp nhận nếu tất cả điều kiện trên thỏa mãn. Ngược lại, xuất từ chối.
Kết luận: Cam kết đa thức là một lớp giao thức mật mã rất quan trọng, được ứng dụng rộng rãi trong nhiều hệ thống mật mã, đặc biệt là hệ thống chứng minh kiến thức không tiết lộ. Bài viết này trình bày chi tiết giao thức cam kết đa thức Brakedown cùng các kiến thức toán học liên quan, là thành phần nền tảng quan trọng của FOAKS, đóng vai trò then chốt trong việc cải thiện hiệu suất triển khai thực tế của FOAKS.
Tài liệu tham khảo
-
[GLS+]: Alexander Golovnev, Jonathan Lee, Srinath Setty, Justin Thaler, Riad S. Wahby. Brakedown: Linear-time and post-quantum snarks for r 1 cs. Cryptology ePrint Archive. https://ia.cr/2021/1043.
-
[XZS 22]: Xie T, Zhang Y, Song D. Orion: Zero knowledge proof with linear prover time[C]//Advances in Cryptology–CRYPTO 2022: 42nd Annual International Cryptology Conference, CRYPTO 2022, Santa Barbara, CA, USA, August 15–18, 2022, Proceedings, Part IV. Cham: Springer Nature Switzerland, 2022: 299-328. https://eprint.iacr.org/2022/1010
-
[BCG 20]: Bootle, Jonathan, Alessandro Chiesa, Jens Groth. "Linear-time arguments with sublinear verification from tensor codes." Theory of Cryptography: 18th International Conference, TCC 2020, Durham, NC, USA, November 16–19, 2020, Proceedings, Part II 18. Springer International Publishing, 2020.
-
Justin Thaler từ A16z crypto, Measuring SNARK performance: Frontends, backends, and the future https://a16z crypto.com/measuring-snark-performance-frontends-backends-and-the-future/
-
Giới thiệu về tích tenxơ: https://blog.csdn.net/chenxy_bwave/article/details/127288938
Chào mừng tham gia cộng đồng chính thức TechFlow
Nhóm Telegram:https://t.me/TechFlowDaily
Tài khoản Twitter chính thức:https://x.com/TechFlowPost
Tài khoản Twitter tiếng Anh:https://x.com/BlockFlow_News