Làm thế nào để thiết kế một sơ đồ bằng chứng đệ quy tinh tế và hoàn hảo?

2023.02.21

Chia sẻ đến

Tuyển chọn TechFlowTuyển chọn TechFlow

Làm thế nào để thiết kế một sơ đồ bằng chứng đệ quy tinh tế và hoàn hảo?

Hầu như mọi thách thức gặp phải trong lĩnh vực zkRollup và zkEVM về bản chất đều là vấn đề thuật toán. Việc tăng tốc phần cứng ZKP thường xuyên được nhắc đến chủ yếu là do các thuật toán hiện tại nói chung khá chậm.

2023.02.21 - 05:10:14

ZKP

Chuyên sâu báo cáo Web3

Tác giả: Lâm Diễn Hy, CTO của Fox Tech; Mạnh Huyền Tế, Nhà khoa học trưởng của Fox Tech

Lời mở đầu: Hầu hết các thách thức gặp phải trong lĩnh vực zkRollup và zkEVM về bản chất đều là vấn đề thuật toán. Lý do mà tăng tốc phần cứng cho ZKP được nhắc đến thường xuyên chính là vì các thuật toán hiện tại nói chung khá chậm. Để tránh rơi vào tình trạng "thuật toán không đủ, phần cứng bù đắp", chúng ta cần giải quyết vấn đề ở cấp độ thuật toán cốt lõi. Việc thiết kế một phương án chứng minh đệ quy tinh tế chính là chìa khóa để giải quyết vấn đề này.

Cùng với sự phát triển không ngừng của hợp đồng thông minh, ngày càng nhiều ứng dụng web3 xuất hiện, khối lượng giao dịch trên các nền tảng Layer1 truyền thống như Ethereum tăng nhanh chóng và có thể xảy ra tắc nghẽn bất kỳ lúc nào. Làm thế nào để vừa đảm bảo được tính an toàn từ Layer1 mang lại, vừa đạt được hiệu suất cao hơn đã trở thành vấn đề cấp thiết cần giải quyết.

Đối với Ethereum, zkRollup sử dụng thuật toán bằng chứng kiến thức không (zero-knowledge proof) làm thành phần nền tảng, chuyển những tính toán tốn kém trước đây phải thực hiện trên Layer1 xuống off-chain, đồng thời cung cấp bằng chứng về tính đúng đắn của việc thực thi lên chuỗi. Các dự án tiêu biểu trong lĩnh vực này gồm StarkWare, zkSync, Scroll và Fox Tech.

Thực tế, trong thiết kế zkRollup, yêu cầu về hiệu suất rất cao: mong muốn bằng chứng gửi lên đủ nhỏ để giảm tải tính toán cho Layer1. Để đạt được độ dài bằng chứng tối ưu, các dự án zkRollup đang cải tiến thuật toán và kiến trúc hệ thống. Ví dụ, Fox đã kết hợp thuật toán bằng chứng kiến thức không tiên tiến nhất để phát triển thuật toán chứng minh riêng FOAKS, nhằm đạt được thời gian chứng minh và độ dài bằng chứng tốt nhất.

Ngoài ra, trong giai đoạn xác minh bằng chứng, cách làm đơn giản nhất là tạo và xác minh từng bằng chứng theo thứ tự tuyến tính. Để nâng cao hiệu quả, người ta nghĩ ngay đến việc đóng gói nhiều bằng chứng thành một bằng chứng duy nhất — đây chính là cái gọi là gộp bằng chứng (Proof Aggregation).

Một cách trực quan, việc xác minh bằng chứng được tạo bởi zkEVM là một quá trình tuyến tính, bên xác minh (Verifier) cần lần lượt kiểm tra từng giá trị bằng chứng được tạo ra. Tuy nhiên, cách thức này có hiệu suất thấp và chi phí truyền thông lớn. Trong ngữ cảnh zkRollup, chi phí cao hơn ở phía bên xác minh đồng nghĩa với việc tăng tính toán trên Layer1, dẫn đến phí Gas cao hơn.

Chúng ta hãy xem xét một ví dụ: Alice muốn chứng minh với cả thế giới rằng cô ấy đã đến công viên Fox từ ngày 1 đến ngày 7 trong tháng này. Để làm điều đó, mỗi ngày từ ngày 1 đến ngày 7, cô ấy có thể chụp một bức ảnh tại công viên với tờ báo ngày hôm đó. Bảy bức ảnh này khi gom lại sẽ tạo thành một bằng chứng.

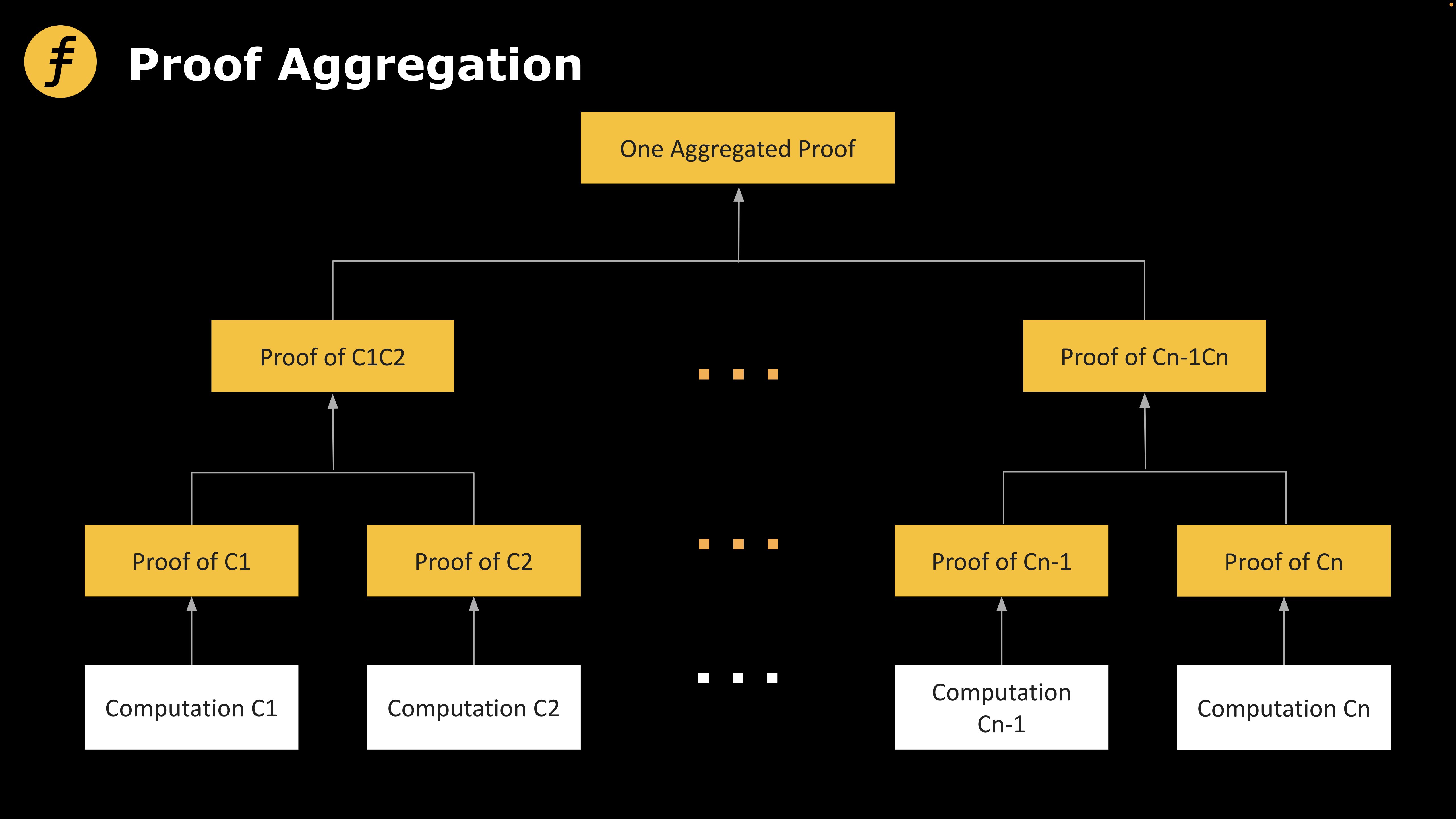
Làm thế nào để thiết kế một phương án chứng minh đệ quy tinh tế?

Hình 1: Sơ đồ gộp bằng chứng theo nghĩa thông thường

Trong ví dụ trên, việc bỏ bảy bức ảnh trực tiếp vào một phong bì chính là hình ảnh hóa khái niệm gộp bằng chứng theo nghĩa thông thường. Trong thực tế, điều này tương đương với việc nối các bằng chứng khác nhau lại với nhau và xác minh tuần tự: trước tiên xác minh bằng chứng đầu tiên, rồi đến bằng chứng thứ hai và các bằng chứng tiếp theo. Vấn đề là cách làm này vừa không thay đổi kích thước bằng chứng, vừa không tiết kiệm thời gian, hiệu quả tương đương với việc xác minh từng bằng chứng một. Nếu muốn đạt được mức độ nén không gian theo cấp logarithm, cần sử dụng kỹ thuật chứng minh đệ quy (Proof Recursion) được đề cập dưới đây.

Phương án chứng minh đệ quy dùng bởi Halo2 và STARK

Để minh họa rõ hơn về chứng minh đệ quy, ta quay lại ví dụ trên.

Bảy bức ảnh của Alice thực chất là bảy bằng chứng. Giờ ta xét đến việc gộp chúng lại: Alice có thể chụp ảnh tại công viên vào ngày 1, sau đó vào ngày 2, cầm theo tấm ảnh ngày 1 và chụp cùng với tờ báo ngày 2; vào ngày 3, lại cầm tấm ảnh ngày 2 và chụp cùng tờ báo ngày 3. Cứ như vậy, đến ngày 7, Alice cầm tấm ảnh ngày 6 và chụp cùng tờ báo ngày 7. Khi những người khác nhìn thấy bức ảnh cuối cùng này vào ngày 7, họ có thể xác minh rằng Alice đã đến công viên từ ngày 1 đến ngày 7. Như vậy, bảy bức ảnh bằng chứng ban đầu đã được nén thành một. Kỹ thuật then chốt trong quá trình này chính là “ảnh chụp chứa ảnh”, tức là lồng ghép ảnh trước đó vào ảnh sau theo dạng đệ quy. Điều này khác với việc đặt nhiều ảnh cạnh nhau rồi chụp lại.

Kỹ thuật chứng minh đệ quy trong zkRollup có thể nén đáng kể kích thước bằng chứng. Cụ thể, mỗi giao dịch sẽ tạo ra một bằng chứng. Gọi mạch tính toán gốc là C0, P0 là bằng chứng tính đúng đắn của C0, V0 là quá trình tính toán để xác minh P0. Bên tạo bằng chứng (Prover) sẽ chuyển đổi V0 thành một mạch tương ứng, ký hiệu là C0’. Khi đó, đối với một giao dịch khác có mạch tính toán C1, có thể gộp C0’ và C1 lại với nhau. Như vậy, chỉ cần xác minh bằng chứng đúng đắn P1 của mạch gộp, đồng nghĩa với việc xác minh tính đúng đắn của cả hai giao dịch — đạt được hiệu quả nén.

Nhìn lại quá trình trên, nguyên lý nén nằm ở việc biến quá trình xác minh bằng chứng thành một mạch, sau đó tạo ra “bằng chứng của bằng chứng”. Vì vậy, xét về mặt này, đây là một thao tác có thể đệ quy liên tục, do đó gọi là chứng minh đệ quy.

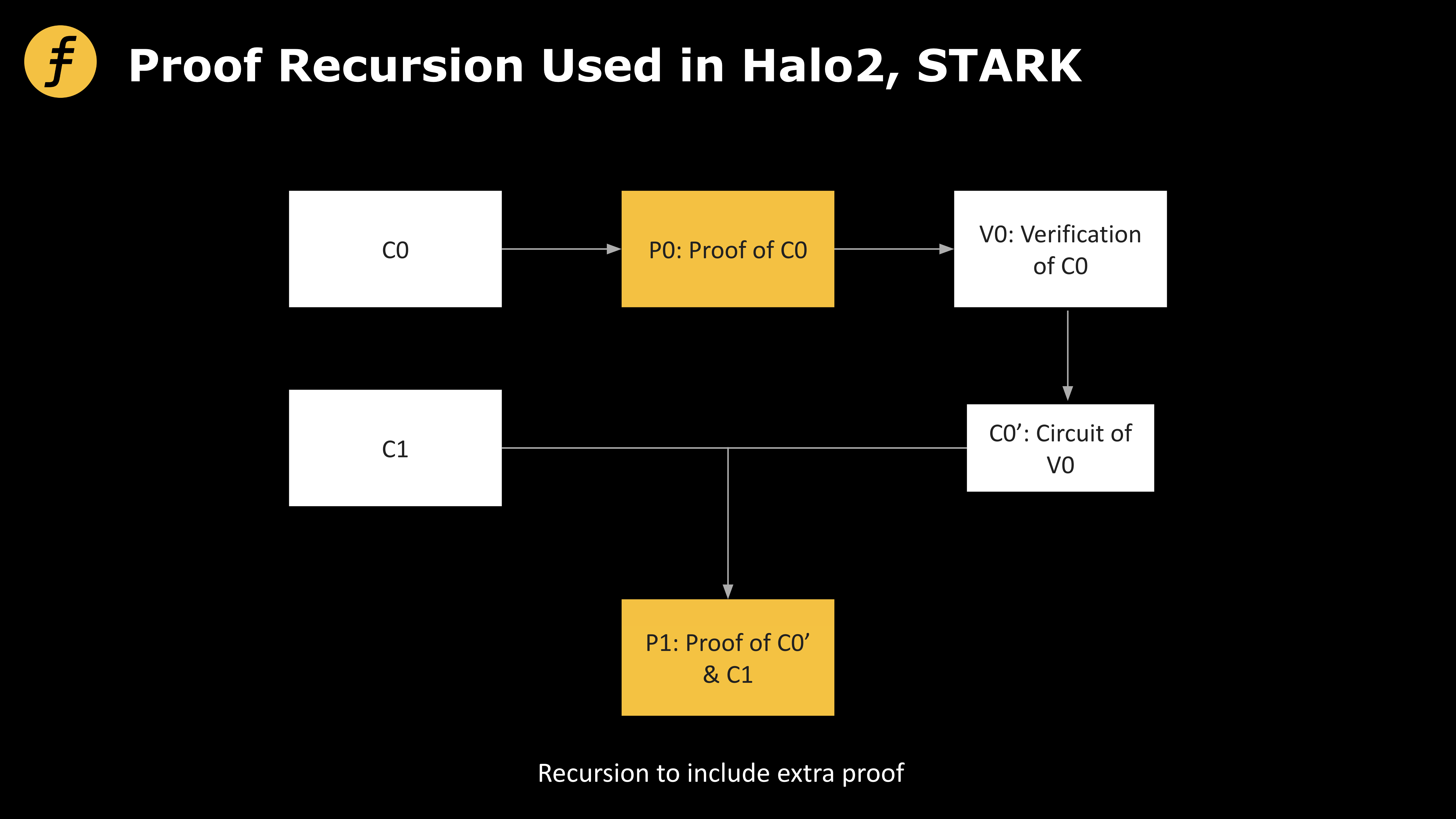
Làm thế nào để thiết kế một phương án chứng minh đệ quy tinh tế?

Hình 2: Phương án chứng minh đệ quy được dùng bởi Halo2 và Stark

Phương án Proof Recursion được áp dụng bởi Halo2 và STARK cho phép tạo bằng chứng song song và gộp nhiều bằng chứng lại, nhờ đó việc xác minh một bằng chứng duy nhất đồng thời xác minh tính đúng đắn của nhiều giao dịch, giúp nén chi phí tính toán và nâng cao đáng kể hiệu suất hệ thống.

Tuy nhiên, tối ưu hóa như vậy vẫn chỉ dừng lại ở tầng trên các thuật toán bằng chứng kiến thức cụ thể. Để nâng cao hiệu quả hơn nữa, chúng ta cần những cải tiến và đột phá ở tầng sâu hơn. Thuật toán FOAKS do Fox thiết kế đã làm được điều này bằng cách áp dụng tư tưởng đệ quy vào bên trong nội bộ một bằng chứng.

Phương án chứng minh đệ quy dùng bởi FOAKS

Fox Tech là một dự án zkRollup dựa trên zkEVM. Trong hệ thống chứng minh của nó, cũng sử dụng kỹ thuật chứng minh đệ quy, nhưng ý nghĩa bên trong khác biệt so với cách đệ quy nói trên. Điểm khác biệt chủ yếu nằm ở chỗ Fox áp dụng tư tưởng đệ quy (Recursion) bên trong nội bộ một bằng chứng. Để diễn tả rõ tư tưởng cốt lõi của chứng minh đệ quy do Fox sử dụng — liên tục rút gọn vấn đề cần chứng minh cho đến khi bài toán rút gọn đủ đơn giản — ta cần đưa thêm một ví dụ.

Trong ví dụ trước, Alice dùng ảnh để chứng minh mình đã đến công viên Fox vào một ngày nào đó. Bob đưa ra một gợi ý khác: ông cho rằng việc chứng minh Alice đã đến công viên có thể được rút gọn thành việc chứng minh chiếc điện thoại của Alice đã đến đó, và việc chứng minh này lại có thể được rút gọn thành việc chứng minh vị trí định vị của điện thoại Alice nằm trong phạm vi công viên. Do đó, để chứng minh Alice đã đến công viên, cô ấy chỉ cần gửi định vị từ điện thoại khi đang ở trong công viên. Như vậy, kích thước bằng chứng đã giảm từ một bức ảnh (một dữ liệu nhiều chiều) xuống còn một dữ liệu ba chiều (kinh độ, vĩ độ và thời gian), tiết kiệm hiệu quả chi phí. Ví dụ này chưa hoàn toàn chính xác, vì có người có thể phản bác rằng điện thoại đến công viên Fox không đồng nghĩa với việc Alice có mặt ở đó. Tuy nhiên, trong thực tế, quá trình rút gọn này là chặt chẽ về mặt toán học.

Cụ thể, cách dùng chứng minh đệ quy của Fox là đệ quy ở cấp độ mạch. Khi thực hiện bằng chứng kiến thức không, ta sẽ chuyển bài toán cần chứng minh thành một mạch, sau đó suy ra một số đẳng thức cần thỏa mãn. Thay vì trực tiếp chứng minh các đẳng thức này được thỏa mãn, ta lại chuyển các đẳng thức này thành một mạch mới, và cứ tiếp tục như vậy, cho đến khi đẳng thức cuối cùng cần chứng minh trở nên đơn giản đủ để có thể chứng minh trực tiếp một cách dễ dàng.

Từ quá trình này, ta thấy rõ cách làm này sát nghĩa “đệ quy” hơn. Cần lưu ý rằng không phải thuật toán nào cũng có thể áp dụng kỹ thuật đệ quy này. Giả sử mỗi lần đệ quy biến một chứng minh có độ phức tạp O(n) thành chứng minh có độ phức tạp O(f(n)), trong khi chi phí tính toán của bản thân quá trình đệ quy là O(g(n)). Khi đó, độ phức tạp tính toán tổng sau một lần đệ quy là O1(n) = O(f(n)) + O(g(n)); sau hai lần là O2(n) = O(f(f(n))) + O(g(n)) + O(g(f(n))); sau ba lần là O3(n) = O(f(f(f(n)))) + O(g(n)) + O(g(f(n))) + O(g(f(f(n)))), v.v. Vì vậy, chỉ khi hai hàm f và g đại diện cho đặc tính thuật toán thỏa mãn điều kiện Ok(n) < O(n) với một giá trị k nào đó thì kỹ thuật đệ quy này mới phát huy hiệu quả. Fox đã vận dụng hiệu quả kỹ thuật đệ quy này để nén độ phức tạp của bằng chứng.

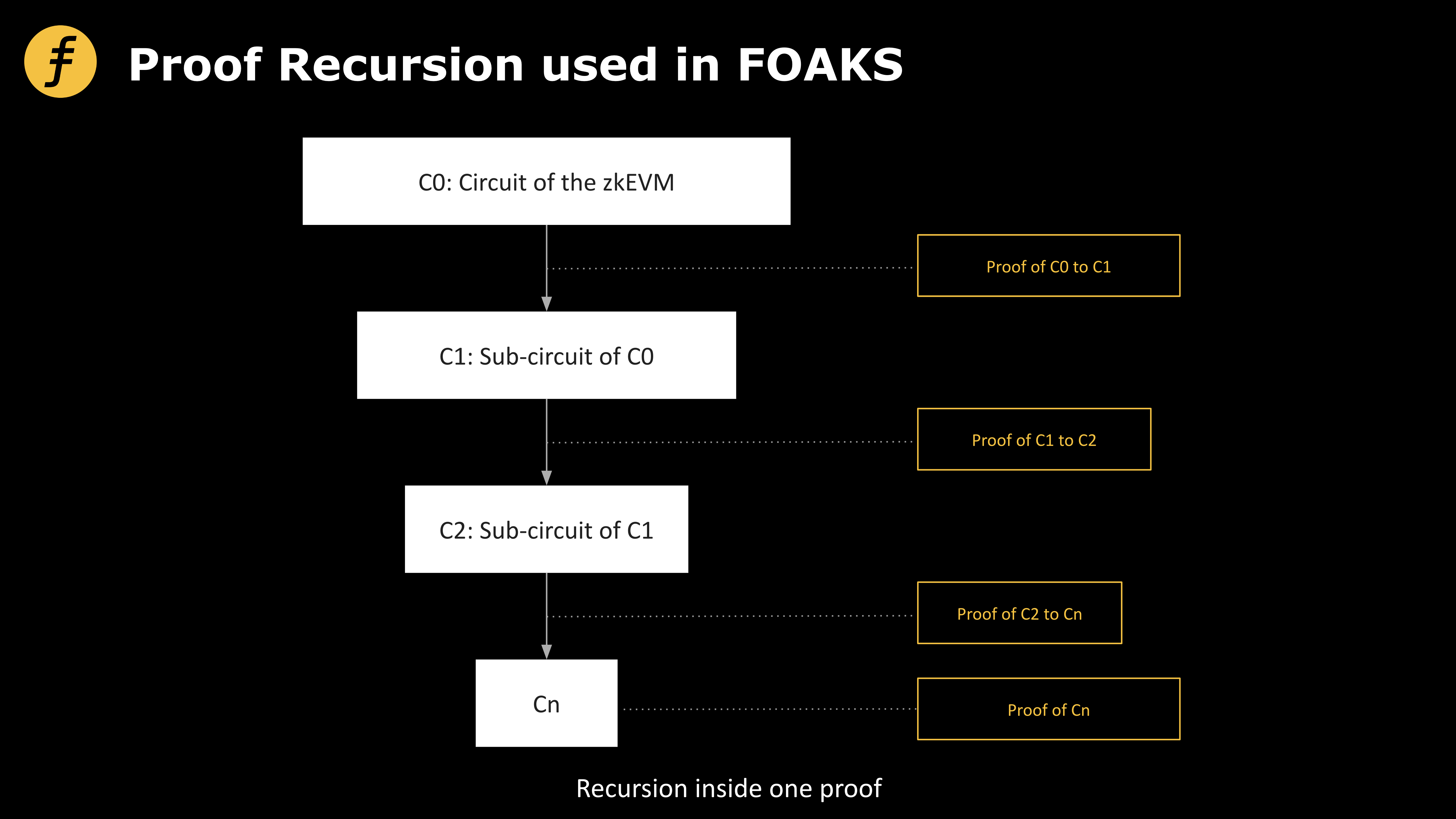
Làm thế nào để thiết kế một phương án chứng minh đệ quy tinh tế?

Hình 3: Phương án chứng minh đệ quy được dùng bởi ZK-FOAKS

Kết luận

Độ phức tạp của bằng chứng luôn là một trong những yếu tố then chốt quan trọng nhất trong ứng dụng bằng chứng kiến thức không. Đặc tính này ngày càng trở nên quan trọng khi các vấn đề cần chứng minh ngày càng phức tạp, đặc biệt trong các kịch bản ZK khổng lồ như zkEVM, nơi độ phức tạp của bằng chứng ảnh hưởng quyết định đến hiệu năng sản phẩm và trải nghiệm người dùng. Trong số nhiều phương pháp giảm độ phức tạp của bằng chứng cuối cùng, tối ưu hóa thuật toán cốt lõi là quan trọng nhất. Fox đã thiết kế một phương án chứng minh đệ quy tinh tế dựa trên các thuật toán tiên tiến hàng đầu, và sử dụng công nghệ này để phát triển thuật toán ZK-FOAKS phù hợp nhất cho zkEVM, hứa hẹn trở thành giải pháp hiệu suất hàng đầu trong lĩnh vực zkRollup.