Curve Stablecoin Design Whitepaper: AMM with Continuous Liquidation / No Liquidation
Tuyển chọn TechFlowTuyển chọn TechFlow

Curve Stablecoin Design Whitepaper: AMM with Continuous Liquidation / No Liquidation
Hy vọng cơ chế được đề xuất có thể giải quyết rủi ro thanh lý nhằm mục đích phát hành stablecoin và cho vay.
Tác giả: JamesX, iZUMi Research
Bản dịch tham chiếu tiếng Trung - Anh của bản whitepaper thiết kế stablecoin Curve, kèm theo một số chú thích tiếng Trung hỗ trợ hiểu rõ hơn, đồng thời đã sửa một số lỗi chính tả trong bản gốc, kính mời mọi người tham khảo học tập.
Tổng quan
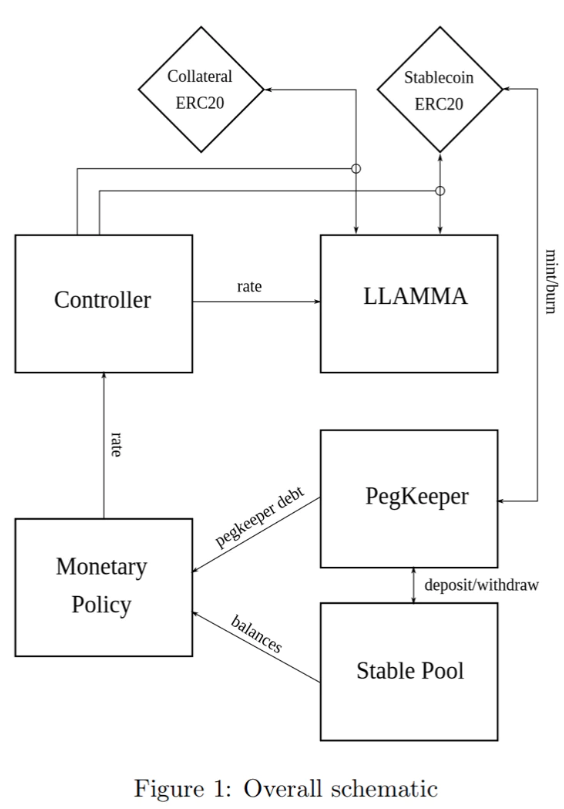
Thiết kế stablecoin này bao gồm một vài khái niệm then chốt: thuật toán AMM cho vay-thanh lý (LLAMMA), PegKeeper (cơ chế duy trì neo giá), và chính sách tiền tệ. Tuy nhiên điểm thiết kế chính nằm ở LLAMMA: dùng một AMM chuyên dụng thay thế quy trình thanh lý truyền thống dựa trên thế chấp vượt mức.
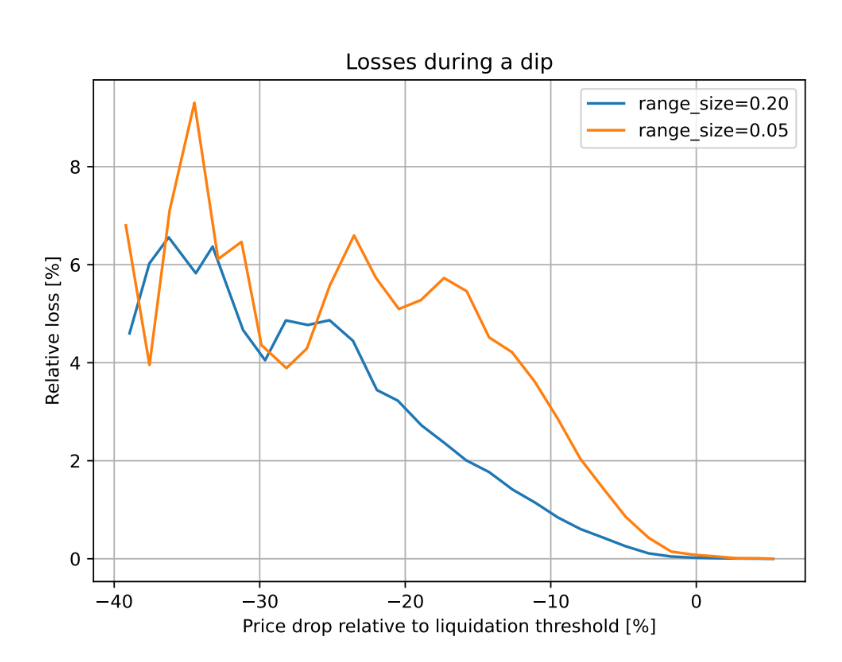
Hình 2: Sự phụ thuộc của tổn thất vào biến động giá tương đối so với ngưỡng thanh lý. Khung thời gian quan sát là 3 ngày.
Trong thiết kế này, nếu có người vay tiền bằng tài sản đảm bảo, ngay cả khi giá tài sản đảm bảo giảm xuống dưới ngưỡng thanh lý rồi phục hồi — cũng sẽ không xảy ra tổn thất đáng kể nào.
Ví dụ, theo mô phỏng dựa trên dữ liệu lịch sử ETH/USD từ tháng 9 năm 2017, nếu để CDP không được quản lý trong 3 ngày, trong thời gian đó giá giảm xuống thấp hơn 10% so với giá thanh lý, thì chỉ có 1% tài sản đảm bảo bị mất.
AMM Thanh lý Liên tục / Không Cần Thanh lý (LLAMMA)
Tư tưởng cốt lõi trong thiết kế stablecoin là thuật toán AMM cho vay-thanh lý (Lending-Liquidating AMM). Ý tưởng này là chuyển đổi giữa tài sản đảm bảo (ví dụ như ETH) và stablecoin (ở đây tạm gọi là USD). Nếu giá tài sản đảm bảo cao — khoản tiền gửi của người dùng toàn bộ là ETH; nhưng khi giá giảm, nó sẽ chuyển dần sang USD stablecoin. Điều này rất khác biệt so với thiết kế AMM truyền thống, vốn đặt stablecoin USD ở phần trên (nửa trên đường cong AMM), và ETH ở phần dưới (nửa dưới đường cong AMM).
Phần mô tả dưới đây không thể coi là một chứng minh hoàn chỉnh và chặt chẽ về mặt logic. Nhiều yếu tố (đặc biệt là các bất biến) được xây dựng từ nhiều góc độ khác nhau. Để có một mô tả toán học đầy đủ, có lẽ cần thêm nghiên cứu, tuy nhiên phần mô tả dưới đây được đánh giá là đủ để triển khai trong hợp đồng thông minh.
Cơ chế này chỉ khả thi nhờ nguồn giá từ oracle bên ngoài. Nói ngắn gọn, nếu ta tạo một AMM điển hình (ví dụ, đường cong dính kết là dạng hyperbol), và "giá trung tâm" của nó di chuyển từ giảm sang tăng, thì token sẽ được chuyển đổi "đoạn nhiệt" từ USD sang ETH, đồng thời cung cấp tính thanh khoản hai chiều trong suốt quá trình (Hình 3). Cơ chế này hơi giống hiện tượng “chéo tránh” (avoided crossing) trong vật lý lượng tử (còn gọi là chuyển tiếp Landau-Zener), dù chỉ mang tính khái niệm — mô tả toán học thực tế có thể rất khác.

Phạm vi tập trung thanh khoản ở đây được gọi là “dải” (band), tại mỗi dải cố định po có thanh khoản từ pcd đến pcu. Ta tìm kiếm pcd(po) và pcu(po) chỉ là hàm của po, với tốc độ tăng nhanh hơn tuyến tính, nghĩa là tăng nhanh hơn po (Hình 4). Ngoài ra, hãy định nghĩa các giá p↓ và p↑ sao cho p↓(po)=po và p↑(po)=po là các đầu mút của dải trong giới hạn đoạn nhiệt (ví dụ p=po).
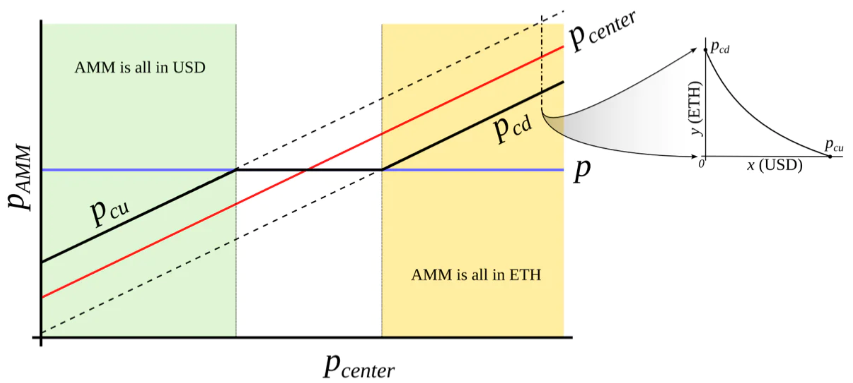
Hình 3: Hành vi của “AMM có nguồn giá bên ngoài”. Giá bên ngoài pcenter xác định vùng giá xung quanh đó thanh khoản được hình thành. AMM hỗ trợ tập trung thanh khoản trong khoảng giá từ pcd đến pcu, với pcd < pcenter < pcu. Khi giá hiện tại p vượt ra ngoài khoảng pcd–pcu, AMM sẽ hoàn toàn chuyển sang stablecoin (khi ở pcu) hoặc hoàn toàn chuyển sang tài sản đảm bảo (khi ở pcd). Khi pcd ≤ p ≤ pcu, giá AMM bằng với giá hiện tại p.
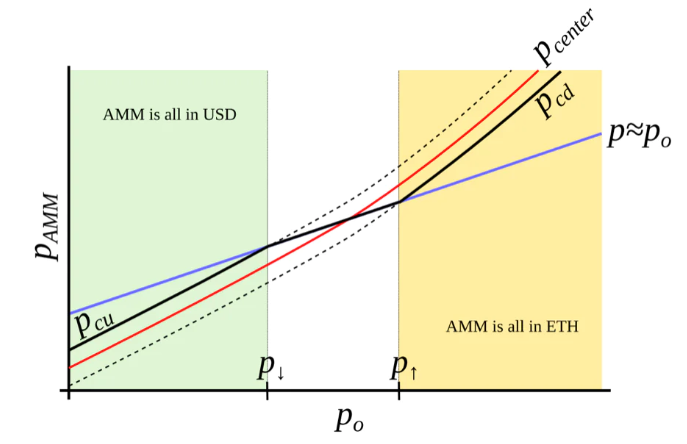
Hình 4: AMM mà chúng ta đang tìm kiếm. Chúng ta muốn xây dựng một AMM mà pcd và pcu là hàm của po, tăng nhanh hơn khi po tăng. Trong trường hợp này, khi ETH đắt, AMM sẽ chuyển hoàn toàn sang ETH; khi ETH rẻ, sẽ chuyển hoàn toàn sang USD.
Chúng ta bắt đầu với một vài dải, tương tự Uniswap V3, giữ nguyên dạng hyperbol của đường cong dính kết bằng cách thêm “số dư ảo”. Giả sử số lượng USD là x, số lượng ETH là y, do đó bất biến tích hằng “tăng cường” sẽ là:

Ta cũng có thể biểu diễn x₀ ≡ x + f và y₀ ≡ y + g, sao cho bất biến trở thành dạng quen thuộc I = x₀y₀. Tuy nhiên, f và g không cố định: chúng thay đổi theo giá oracle bên ngoài (và bất biến I cũng vậy, nên nó chỉ là bất biến khi giá oracle po không đổi). Tại một po nhất định, f và g là cố định trong toàn bộ dải. Như đã nói, ta ký hiệu p↑ là giá đỉnh dải, p↓ là giá đáy dải. Ta định nghĩa A (chỉ số đo mức độ tập trung thanh khoản) như sau:

Thuộc tính ta đang tìm kiếm là: giá po cao hơn phải dẫn đến giá cao hơn tại cùng mức số dư, do đó giá thị trường hiện tại (trung bình sẽ theo po) thấp hơn giá này, và dải sẽ giao dịch theo hướng toàn ETH (và ngược lại). Có thể tìm được nhiều cách thỏa mãn điều kiện này, nhưng ta cần một cách như sau:
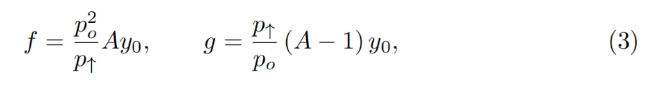
Trong đó y₀ là một đại lượng đo lường khoản tiền gửi hiện tại trong dải, tính theo đơn vị ETH, được định nghĩa như sau: khi giá hiện tại p, p↑ và po bằng nhau, thì y = y₀ và x = 0 (xem điểm po = p↑ trên Hình 4). Vậy nếu thay y tại thời điểm đó:

Giá bằng dx₀/dy₀, do đó với bất biến tích hằng sẽ là:
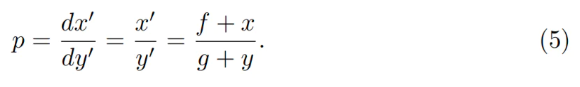
Ta có thể thay x=0 hoặc y=0 để kiểm tra tính nhất quán của công thức trên trong các trường hợp po=p↑ hoặc po=p↓.
Thông thường với một dải, ta biết p↑, do đó cũng biết p↓, po, hằng số A, và x, y (tiền gửi hiện tại trong dải). Để tính tất cả những thứ còn lại, ta cần tìm y₀. Nó có thể được tìm bằng cách giải phương trình bậc hai của bất biến:
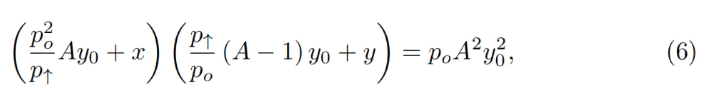
Điều này trở thành phương trình bậc hai theo y₀:
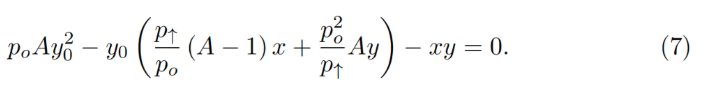
Trong hợp đồng thông minh, ta giải phương trình bậc hai này trong hàm get_y0.
Khi giá oracle po không đổi, AMM hoạt động theo cách thông thường, ví dụ bán ETH khi giá lên/mua ETH khi giá xuống. Bằng cách đơn giản thay x=0 vào phương trình bất biến để tìm giá "hiện tại xuống" pcd, hoặc thay y=0 để tìm giá "hiện tại lên" pcu, ta có thể suy ra giá AMM tại giá trị hiện tại của po và p↑ là:
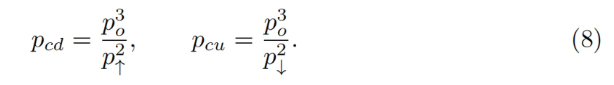
Một vấn đề thực tiễn quan trọng khác: nếu giá thay đổi chậm đến mức giá oracle po có thể "đoạn nhiệt" theo kịp hoàn toàn (trong một dải), thì với x và y hiện tại, bắt đầu từ p=po, dải cuối cùng sẽ nhận được bao nhiêu ETH (y↑) nếu giá tăng, hoặc bao nhiêu USD (x↓) nếu giá giảm? Mặc dù đây không phải là bài toán toán học dễ giải ngay lập tức, nhưng tính toán số học cho thấy một câu trả lời khá đơn giản:

Khi đánh giá độ an toàn của khoản vay và tổn thất tiềm tàng của AMM, ta sẽ dùng các kết quả này.
Giờ ta đã có mô tả cho một dải. Ta chia toàn bộ không gian giá thành các dải, sao cho các giá p↓ và p↑ của các dải kề nhau tiếp xúc nhau. Vì vậy, nếu ta đặt một giá cơ sở pbase và một số hiệu dải n:
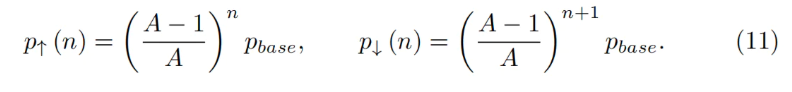
Với bất kỳ dải nào, có thể chứng minh rằng nghiệm của công thức 7 và công thức 5 đều thỏa mãn:
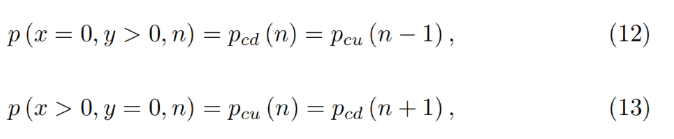
Điều này cho thấy không có khe hở giữa các dải.
Giao dịch xảy ra đồng thời vẫn giữ bất biến theo công thức 1, tuy nhiên, khi giá là po, giá nội bộ hiện tại trong AMM sẽ thay đổi: khi po giảm, nó sẽ tăng lên, và ngược lại (theo hệ số lập phương), như thấy từ công thức 8.
LLAMMA vs Stablecoin
Stablecoin là một CDP, nơi người dùng vay stablecoin bằng tài sản đảm bảo biến động (tiền mã hóa, ví dụ như ETH). Tài sản đảm bảo được nạp vào phạm vi giá của LLAMMA (các dải như vậy), nếu giá tài sản đảm bảo giảm chậm tương đối, ETH sẽ được chuyển đổi thành đủ stablecoin để thanh toán đóng CDP (việc này có thể xảy ra qua tự thanh lý, hoặc qua thanh lý bên ngoài nếu tỷ lệ thế chấp quá gần giới hạn nguy hiểm, hoặc thậm chí không đóng, mà chờ giá phục hồi).
Khi người dùng gửi tài sản đảm bảo và vay một stablecoin, hợp đồng thông minh LLAMMA sẽ tính toán dải mà tài sản đảm bảo nằm trong đó. Khi giá tài sản đảm bảo thay đổi, nó bắt đầu được chuyển đổi sang stablecoin. Khi hệ thống ở trạng thái "chìm dưới nước", người dùng đã có đủ USD để trả khoản vay. Số lượng stablecoin có thể nhận được có thể được tính bằng phương pháp công khai get_x_down. Nếu giá trị đưa ra quá gần ngưỡng thanh lý — người thanh lý bên ngoài có thể tham gia (thường không nên xảy ra trong vài ngày hay vài tuần sau khi giá tài sản đảm bảo giảm và đi ngang, và thậm chí nếu giá tài sản đảm bảo chưa từng tăng hoặc phục hồi tương đối nhanh, thì có thể sẽ không bao giờ xảy ra). Khi giá cách xa "thanh lý", một phương pháp lành mạnh sẽ trả về tỷ lệ giữa get_x_down và nợ vay, cộng thêm giá trị gia tăng của tài sản đảm bảo.
Khi một stablecoin thu lãi suất, điều này cần được phản ánh trong AMM. Cũng cần được phản ánh. Việc này đạt được bằng cách điều chỉnh toàn bộ lưới giá. Do đó, khi một stablecoin thu lãi suất r, tất cả các mức giá trong AMM đều dịch chuyển lên trên với cùng lãi suất r, thông qua một hệ số nhân giá cơ sở. Vì vậy, miễn là lãi suất thu được là dương, hệ số nhân sẽ tăng dần theo thời gian.
Khi ta tính get_x_down hoặc get_y_up, trước tiên ta tìm số lượng stablecoin và tài sản đảm bảo x* và y* nếu giá hiện tại di chuyển đến po. Sau đó ta xem xét, nếu po thay đổi đoạn nhiệt đến giá thấp nhất của dải thấp nhất, hoặc cao nhất của dải cao nhất, ta sẽ nhận được bao nhiêu stablecoin hoặc tài sản đảm bảo tương ứng. Như vậy, ta có được một thước đo về lượng stablecoin sẽ nhận được, không phụ thuộc vào giá tức thời hiện tại — điều này rất quan trọng để chống lại các cuộc tấn công sandwich.
Cần lưu ý rằng LLAMMA sử dụng po định nghĩa là giá ETH/USD làm nguồn giá, trong khi stablecoin của chúng ta có thể giao dịch dưới mức neo (ps < 1) hoặc trên mức neo (ps > 1). Nếu ps < 1, thì giá trong LLAMMA là p > po.
Trong xấp xỉ đoạn nhiệt, p = po/ps, mọi chuyển đổi giữa tài sản đảm bảo và stablecoin sẽ xảy ra ở mức giá oracle cao hơn / giống như mức giá oracle thấp hơn và bằng:
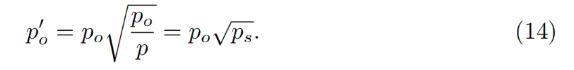
Tại mức giá này, số lượng stablecoin nhận được khi chuyển đổi sẽ cao hơn một hệ số 1/ps (nếu ps < 1).
Trong dài hạn, việc ps > 1 là không lý tưởng, vì vậy chúng ta sẽ sử dụng bộ ổn định (xem chương tiếp theo).
Bộ ổn định tự động và chính sách tiền tệ
Khi ps > 1 (ví dụ do nhu cầu stablecoin tăng), sẽ hình thành dự trữ neo, được tạo bởi việc nạp không đối xứng stablecoin và tiền chuộc được hoặc token LP vào pool stableswap của Curve. Ngay khi ps > 1, hợp đồng PegKeeper được phép đúc stablecoin không có tài sản đảm bảo, và chỉ nạp một chiều vào pool stableswap, sao cho giá cuối cùng vẫn không thấp hơn 1. Khi ps < 1, PegKeeper được phép rút (không đối xứng) và đốt stablecoin.
Những hành vi này khiến giá ps nhanh chóng giảm khi trên 1, và tăng khi dưới 1, vì việc nạp/rút không đối xứng làm thay đổi giá. Ngay cả khi phần “đúc tiền” này không có tài sản đảm bảo, nhưng stablecoin dường như được hỗ trợ ngầm bởi tính thanh khoản trong pool stablecoin. Toàn bộ chu kỳ đúc/đốt cuối cùng dường như sinh lợi, đồng thời mang lại sự ổn định.
Hãy ký hiệu số lượng stablecoin được đúc cho bộ ổn định (nợ) là dst, và ký hiệu hàm fdx() là hàm tính số lượng USD có thể chuộc được cần thiết để mua stablecoin trong hàm get_dx của AMM stableswap. Sau đó, để giữ cho “dự trữ” không quá lớn, ta sử dụng cơ chế ổn định “chậm” bằng cách thay đổi lãi suất vay r.

Trong đó h là biến thiên của ps, và tốc độ thay đổi của r gấp đôi (ps càng cao thì r càng thấp). Số lượng nợ dst của bộ ổn định sẽ cân bằng tại các giá trị khác nhau với tốc độ ps=1 r0. Do đó, ta có thể (thay vì thiết lập thủ công) giảm r0 khi dst/supply vượt quá một ngưỡng mục tiêu nhất định (ví dụ 5%) — nhằm khuyến khích người vay đi vay và bán ra stablecoin, hạ giá và buộc hệ thống đốt dst; hoặc tăng r0 khi thấp hơn — nhằm khuyến khích người vay trả nợ và đẩy ps lên, buộc hệ thống tăng nợ dst và tiền gửi bộ ổn định.
Tổng kết
Hy vọng cơ chế đề xuất có thể giải quyết được rủi ro thanh lý trong việc tạo ra stablecoin và cho vay.
Ngoài ra, cơ chế bộ ổn định và chính sách tiền tệ tự động có thể giúp duy trì neo giá, mà không cần duy trì một PSM (Peg Stability Module – Mô-đun Ổn định Neo giá) quá lớn.
Chào mừng tham gia cộng đồng chính thức TechFlow
Nhóm Telegram:https://t.me/TechFlowDaily
Tài khoản Twitter chính thức:https://x.com/TechFlowPost
Tài khoản Twitter tiếng Anh:https://x.com/BlockFlow_News