어떻게 하면 뛰어난 재귀 증명 방식을 설계할 수 있을까?
글: Fox Tech CTO 임연서, Fox Tech 수석 과학자 맹현제
서론: zkRollup 및 zkEVM 분야에서 직면하는 거의 모든 난제들은 본질적으로 알고리즘 문제이다. ZKP 하드웨어 가속이 자주 언급되는 주된 이유는 현재의 알고리즘이 일반적으로 느리기 때문이다. "알고리즘이 부족하면 하드웨어로 보완한다"는 어색한 상황을 피하기 위해 우리는 근본적인 알고리즘 차원에서 문제를 해결해야 한다. 정교하고 뛰어난 재귀적 증명 방식(recursive proof scheme)을 설계하는 것이 이러한 문제를 해결하는 핵심이다.
스마트 계약의 지속적인 발전과 함께 점점 더 많은 Web3 애플리케이션이 등장하고 있으며, 이더리움 등의 전통적인 레이어1(Layer1)의 거래량이 급증하며 언제든지 혼잡이 발생할 수 있다. 레이어1이 제공하는 보안성을 유지하면서도 더 높은 효율성을 확보하는 방법은 시급히 해결되어야 할 과제가 되었다.
이더리움의 경우 zkRollup은 제로지식 증명(Zero-Knowledge Proof, ZKP) 알고리즘을 기반 구성 요소로 사용하여 원래 레이어1에서 수행해야 했던 고비용 연산을 오프체인으로 이전하고, 체인상에는 실행의 정확성에 대한 증명만을 제출한다. 이 분야의 주요 프로젝트로는 StarkWare, zkSync, Scroll, 그리고 Fox Tech 등이 있다.
사실 zkRollup 설계에서는 효율성에 매우 높은 요구가 존재한다. 즉, 제출되는 증명값이 충분히 작기를 바라며, 이를 통해 레이어1의 계산 부하를 줄일 수 있다. 충분히 작은 증명 길이를 얻기 위해 각 zkRollup 프로젝트들은 알고리즘과 아키텍처 설계를 개선하고 있는데, 예를 들어 Fox는 최신 제로지식 증명 알고리즘을 결합해 자체 증명 알고리즘인 FOAKS를 개발함으로써 최적의 증명 시간과 증명 길이를 달성했다.
또한 증명 검증 단계에서 가장 기본적인 방법은 선형적으로 증명을 생성하고 순차적으로 검증하는 것이다. 효율성을 높이기 위해 사람들은 여러 증명을 하나의 증명으로 묶는 것을 먼저 떠올렸으며, 이것이 일반적으로 말하는 증명 집계(Proof Aggregation)이다.
직관적으로 설명하자면, zkEVM이 생성한 증명을 검증하는 것은 선형적인 과정이다. 검증자(Verifier)는 생성된 각 증명값을 차례로 검증해야 한다. 그러나 이러한 검증 방식은 효율성이 낮고 통신 오버헤드도 크다. zkRollup 시나리오에서 검증자 측의 비용이 더 크다는 것은 레이어1에서의 계산량이 더 많아진다는 의미이며, 결국 더 높은 가스비(Gas fee)를 초래하게 된다.
예를 들어보자. 앨리스(Alice)는 자신이 이번 달 1일부터 7일까지 매일 Fox 공원에 갔음을 세상에 증명하고 싶다. 이를 위해 그녀는 1일부터 7일까지 매일 해당 날짜의 신문을 들고 공원에서 사진을 찍을 수 있으며, 이 7장의 사진을 묶어 하나의 증명으로 만들 수 있다.
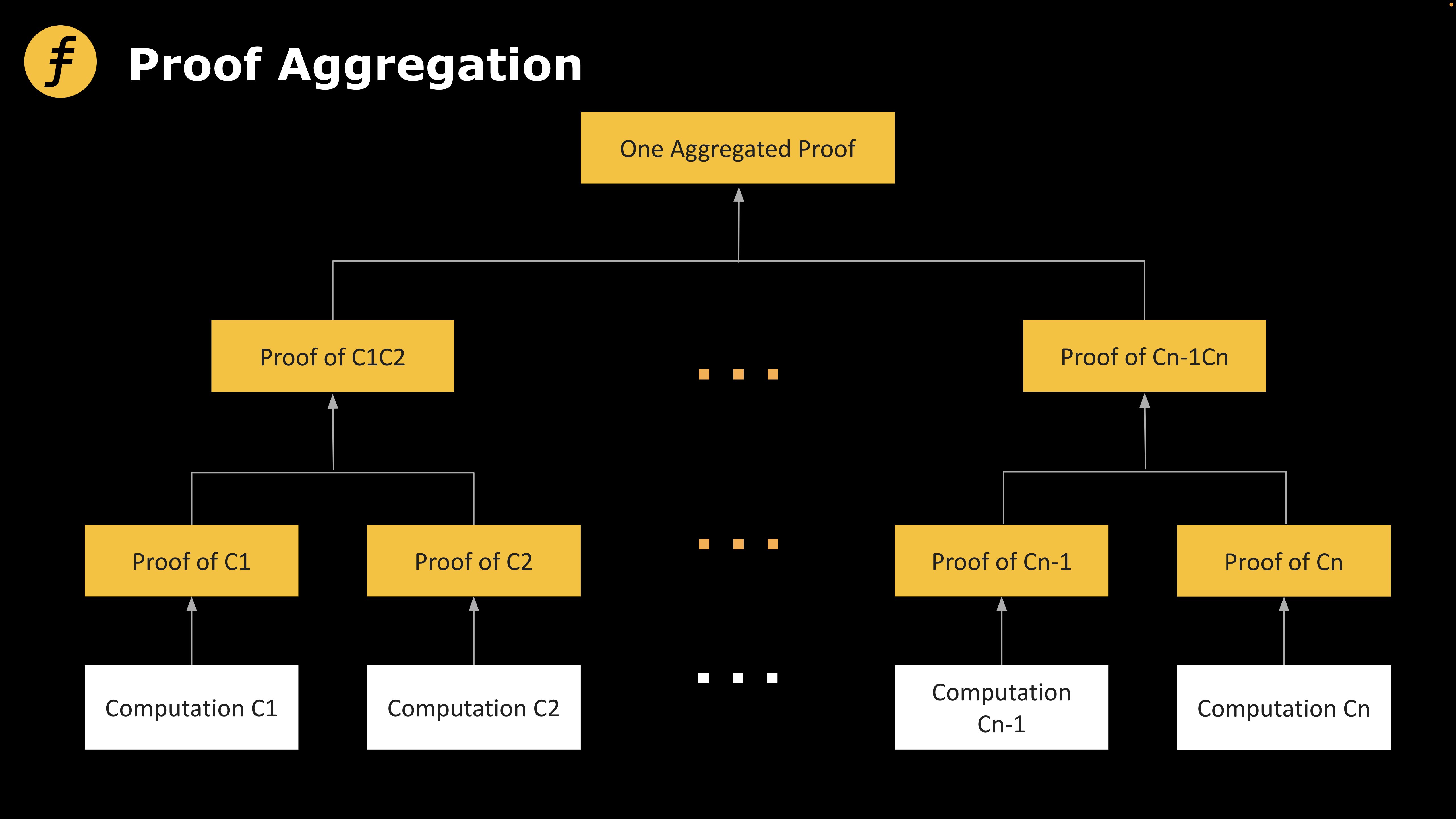
그림 1: 일반적인 증명 집계 방식
위 예시에서 7장의 사진을 그냥 한 봉투에 넣는 것은 직관적인 의미의 증명 집계이며, 실제 상황에서는 서로 다른 증명들을 연결하여 순차적으로 선형 검증하는 것과 같다. 즉, 먼저 첫 번째 증명을 검증하고, 다음 두 번째 증명, 이후의 증명들을 차례로 검증하는 것이다. 문제는 이러한 방식은 증명의 크기와 시간 모두 변화시키지 못하며, 일일이 증명하고 검증하는 것과 동일한 효과를 낸다는 점이다. 로그 차원의 공간 압축을 실현하려면 아래에서 언급할 재귀적 증명(Proof Recursion)을 사용해야 한다.
Halo2 및 STARK에서 사용하는 재귀적 증명 방식
재귀적 증명이 무엇인지 더 잘 설명하기 위해 다시 위의 예시로 돌아가자.
앨리스의 7장의 사진은 실제로 7개의 증명이다. 이제 이들을 병합해보자. 앨리스는 1일에 사진을 찍은 후, 2일에는 그 사진과 2일자의 신문을 들고 다시 사진을 찍고, 3일에는 2일에 찍은 사진과 3일자의 신문을 들고 사진을 찍는다. 이런 식으로 계속해서 7일에는 6일의 사진과 7일자의 신문을 들고 마지막 사진을 찍는다. 그러면 다른 사람들이 7일자의 이 마지막 사진만 보고도 1일부터 7일까지 앨리스가 공원에 갔음을 검증할 수 있다. 이렇게 이전의 일곱 장의 증명 사진이 한 장으로 압축된 것이다. 이 과정의 핵심 기술은 바로 "사진 속의 사진"인데, 이전 사진을 재귀적인 형태로 이후 사진 안에 중첩시키는 것이다. 이것은 여러 장의 사진을 모아서 다시 한 번 찍는 것과는 다르다.
zkRollup의 재귀적 증명 기술은 증명 크기를 크게 축소할 수 있다. 구체적으로, 각 거래마다 하나의 증명이 생성되며, 원래의 거래 계산 회로를 C0, C0의 정확성 증명을 P0, P0을 검증하는 계산 과정을 V0이라고 하자. 증명자(Prover)는 V0도 해당하는 회로로 변환하여 C0'라고 표기한다. 이때 다른 거래의 증명 계산 과정 C1에 대해 C0'과 C1의 회로를 병합할 수 있다. 이렇게 병합된 회로의 정확성 증명 P1을 검증하면 두 거래의 정확성도 동시에 검증된 셈이 되며, 이로써 압축이 이루어지는 것이다.
위 과정을 되돌아보면, 압축의 원리는 증명 검증 과정 자체를 다시 회로로 전환한 후 '증명에 대한 증명'을 생성하는 데 있다. 이런 관점에서 보면, 무한히 아래로 재귀적으로 진행 가능한 작업이므로 재귀적 증명이라 불린다.
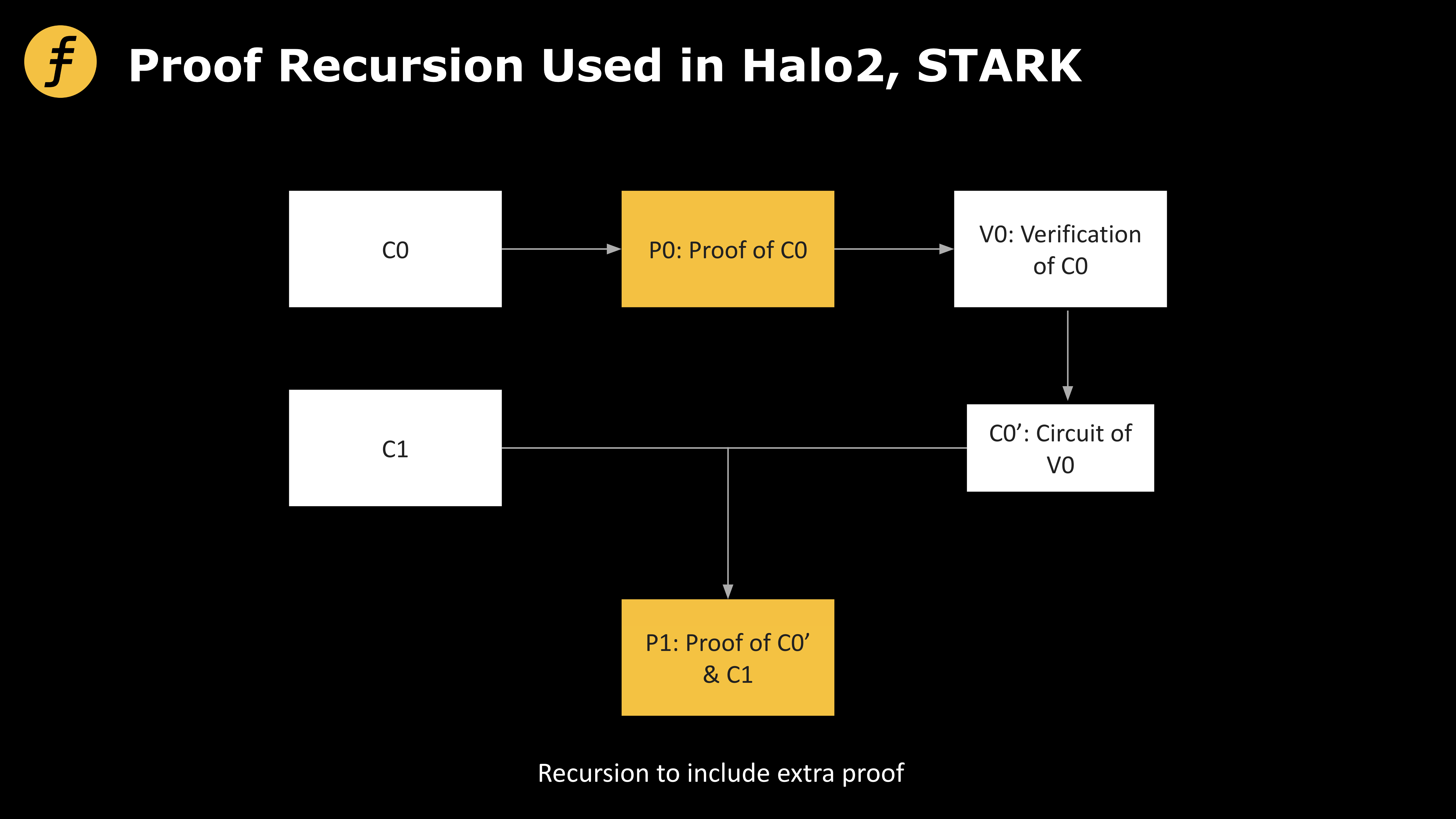
그림 2: Halo2와 Stark가 사용하는 재귀적 증명 방식
Halo2와 STARK가 채택한 Proof Recursion 방식은 증명을 병렬로 생성하고 여러 증명을 병합할 수 있어, 하나의 증명값을 검증함으로써 여러 거래 실행의 정확성을 동시에 검증할 수 있게 해준다. 이를 통해 계산 비용을 압축하여 시스템의 효율성을 극대화할 수 있다.
그러나 이러한 최적화는 여전히 특정 제로지식 증명 알고리즘 상위 수준에 머무르고 있다. 효율성을 더욱 높이기 위해서는 더 낮은 수준의 최적화와 혁신이 필요하다. Fox가 설계한 FOAKS 알고리즘은 재귀적 사고방식을 증명 내부에 적용함으로써 이를 실현했다.
FOAKS가 사용하는 재귀적 증명 방식
Fox Tech는 zkEVM 기반의 zkRollup 프로젝트이다. 그들의 증명 시스템에서도 재귀적 증명 기법을 사용하지만, 그 내포는 앞서 설명한 재귀 방식과는 차이가 있으며, 주요 차이점은 Fox가 증명 내부에서 재귀(Recursion) 개념을 사용한다는 점이다. Fox가 사용하는 재귀적 증명 방식이 문제를 계속해서 축약(reduce)하여 결국 축약된 문제가 충분히 단순해지는 핵심 아이디어를 표현하기 위해, 또 다른 예를 들어보겠다.
앞의 예시에서 앨리스는 사진을 찍어 특정 날짜에 Fox 공원에 갔음을 증명했고, 이에 대해 밥(Bob)이 다른 제안을 했다. 그는 앨리스가 공원에 갔음을 증명하는 문제를 앨리스의 휴대폰이 그 공원에 갔음을 증명하는 문제로 축약할 수 있다고 생각했다. 그리고 이것을 다시 앨리스 휴대폰의 위치 정보가 공원 범위 내에 있었음을 증명하는 것으로 축약할 수 있다고 보았다. 따라서 앨리스가 공원에 갔음을 증명하기 위해, 그녀는 공원에 있을 때 자신의 휴대폰으로 위치 정보를 전송하기만 하면 된다. 이렇게 증명의 크기는 원래의 사진(매우 고차원 데이터)에서 3차원 데이터(경도, 위도, 시간)로 줄어들어 비용을 효과적으로 절감할 수 있다. 이 예시는 완벽하지 않다. 왜냐하면 누군가 앨리스의 휴대폰이 Fox 공원에 갔다고 해서 앨리스 본인이 갔다고 볼 수는 없다고 반박할 수 있기 때문이다. 그러나 실제 상황에서는 이러한 축약 과정은 수학적으로 엄격하게 이루어진다.
구체적으로 말하면, Fox의 재귀적 증명 활용은 회로 수준에서의 재귀이다. 제로지식 증명을 수행할 때, 증명하고자 하는 문제를 회로로 작성한 후, 회로 계산을 통해 만족해야 하는 몇 가지 등식을 도출한다. 이러한 등식들이 만족됨을 보여주는 대신, 우리는 다시 그 등식들을 회로로 작성하고, 이를 반복하여 마침내 증명해야 할 등식이 충분히 단순해질 때까지 진행한 후, 이를 쉽게 직접 증명할 수 있게 된다.
이러한 과정을 통해 우리는 이것이 '재귀'라는 용어의 의미에 훨씬 더 가깝다는 것을 알 수 있다. 주목할 점은 모든 알고리즘이 이 재귀 기술을 사용할 수 있는 것은 아니라는 것이다. 만약 각 재귀 단계에서 복잡도 O(n)의 증명을 O(f(n))의 증명으로 변환한다고 하고, 재귀 과정 자체의 계산 복잡도가 O(g(n))이라면, 한 번 재귀 후의 총 계산 복잡도는 O₁(n) = O(f(n)) + O(g(n))이 되며, 두 번째 재귀 후는 O₂(n) = O(f(f(n))) + O(g(n)) + O(g(f(n))), 세 번째 후는 O₃(n) = O(f(f(f(n)))) + O(g(n)) + O(g(f(n))) + O(g(f(f(n))))이며, 이와 같이 계속된다. 따라서 f와 g라는 두 함수가 특정 k에 대해 Oₖ(n) < O(n)을 만족할 때만 이러한 재귀 기술이 효과적으로 작용할 수 있다. Fox는 이러한 재귀 기술을 효과적으로 활용하여 증명 복잡도를 압축하고 있다.
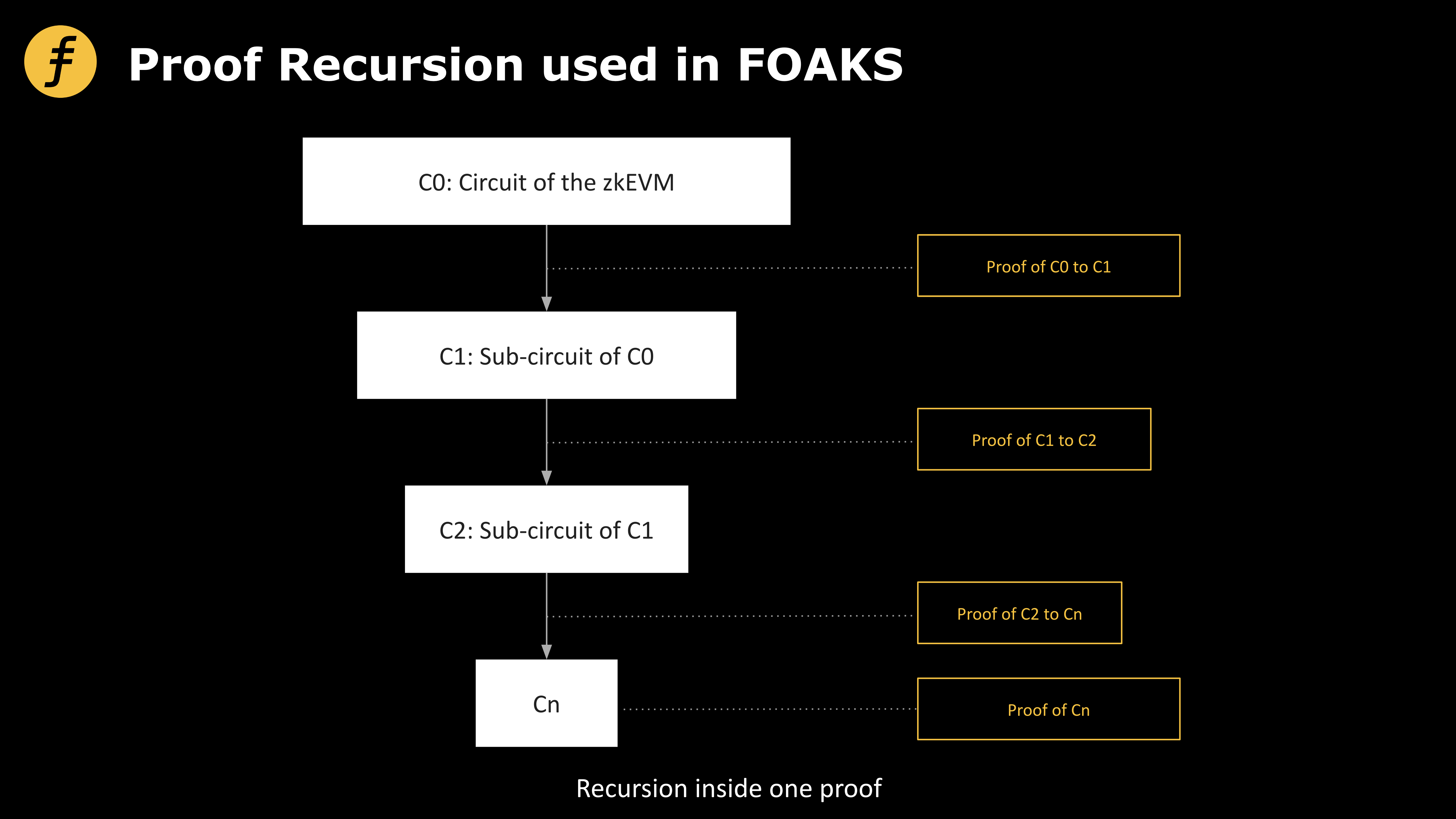
그림 3: ZK-FOAKS가 사용하는 재귀적 증명 방식
마치며
증명의 복잡도는 항상 제로지식 증명 응용에서 가장 중요한 핵심 요소 중 하나이다. 증명 복잡도는 증명 대상이 점점 더 복잡해짐에 따라 중요성이 더욱 커지며, 특히 zkEVM과 같은 거대한 제로지식 응용 시나리오에서는 증명의 복잡도가 제품 성능과 사용자 경험에 결정적인 영향을 미친다. 최종 증명의 복잡도를 줄이는 다양한 방법 중 핵심 알고리즘의 최적화가 가장 중요하다. Fox는 최첨단 알고리즘 기반 위에서 정교하고 뛰어난 재귀적 증명 방식을 설계하였으며, 이를 활용해 zkEVM에 가장 적합한 ZK-FOAKS 알고리즘을 개발함으로써 zkRollup 분야의 성능 리더가 될 가능성을 가지고 있다.
참고 문헌
TechFlow 공식 커뮤니티에 오신 것을 환영합니다
Telegram 구독 그룹:https://t.me/TechFlowDaily
트위터 공식 계정:https://x.com/TechFlowPost
트위터 영어 계정:https://x.com/BlockFlow_News