
Vitalik:プロトコル設計におけるカプセル化された複雑さとシステム全体の複雑さ
TechFlow厳選深潮セレクト

Vitalik:プロトコル設計におけるカプセル化された複雑さとシステム全体の複雑さ
カプセル化の複雑さを適度に支援し、具体的な状況で私たちの判断力を訓練する。
執筆:Vitalik Buterin、イーサリアム共同創設者
翻訳:南風、Unitimes
イーサリアムプロトコル設計の主な目的の一つは、複雑性を最小限に抑えることである。可能な限りプロトコルをシンプルに保ちつつ、ブロックチェーンネットワークとして果たすべき機能をすべて実現できるようにすること。TechFlowはまだ完璧ではなく、特に2014〜2016年に設計された多くの部分において、当時の理解がはるかに少なかったため、より複雑になってしまっている。しかし、我々は依然として複雑性の低減に向けて積極的に努力している。
だが、この目標には課題がある。複雑性とはそもそも定義が難しく、しばしば異なる種類の複雑性とコストを伴う選択肢の間で取引を行う必要がある。では、どのように比較すればよいのか?
複雑性についてより精緻に考えるための強力な知的ツールが一つある。それが、「カプセル化された複雑性(encapsulated complexity)」と「体系的複雑性(systemic complexity)」との区別である。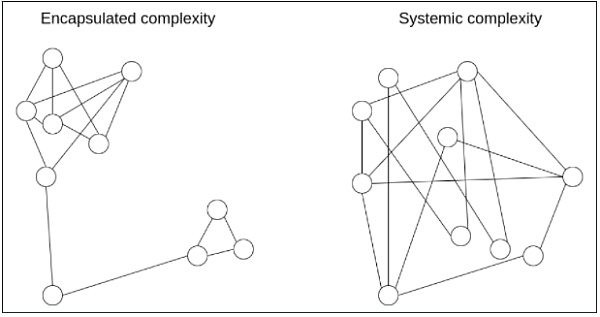
あるサブシステムの内部は複雑でも、外部に対してシンプルな「インターフェース」(interface)を提供する場合、その複雑性は「カプセル化された複雑性」となる。一方、システムの異なる部分が明確に分離できず、互いに複雑に相互作用する場合、「体系的複雑性」が生じる。
以下にいくつかの例を示す。
BLS署名 vs. Schnorr署名
BLS署名とSchnorr署名は、楕円曲線を用いて構成される二つの一般的な暗号署名方式である。
BLS署名の数学的表現は非常にシンプルに見える:
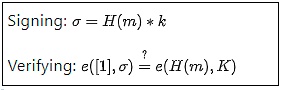
H はハッシュ関数、m はメッセージ、k と K はそれぞれ秘密鍵と公開鍵である。ここまでは簡単だ。しかし、真の複雑性はe関数の定義に隠されている。つまり「楕円曲線ペアリング(elliptic curve pairings)」であり、これは暗号学の中でも最も理解しにくい数学的要素の一つである。
次に、Schnorr署名を見てみよう。Schnorr署名は基本的な楕円曲線のみに依存している。ただし、署名および検証のロジックはやや複雑である:

それでは…どちらの署名方式が「より単純」だろうか?それは、何を重視するかによる! BLS署名は巨大な技術的複雑性を持つが、その複雑性はすべてe関数の定義内に閉じ込められている。もしe関数をブラックボックスと見なせば、BLS署名は実際には非常にシンプルである。一方、Schnorr署名は全体的な複雑性が低いが、部品が多く、外部世界と微妙に相互作用する。
例えば:
-
BLSマルチ署名(二つの鍵 k1 と k2 の組み合わせ署名)は非常に簡単:σ1+σ2 を計算するだけ。しかし、Schnorrマルチ署名は2ラウンドのやり取りを必要とし、厄介なKey Cancellation攻撃への対処も必要になる。
-
Schnorr署名は乱数生成が必要だが、BLS署名は不要である。
楕円曲線ペアリングはしばしば強力な「複雑性スポンジ」として機能する。なぜなら、大量のカプセル化された複雑性を内包しつつ、結果として体系的複雑性を減らすことができるからである。これは多項式コミットメントの領域にも当てはまる:ペアリングを必要とするKZGコミットメントの簡潔さと、ペアリングを必要としない内積証明(inner product arguments)の複雑な内部ロジックを比較してみよ。
暗号学 vs. 暗号経済学
多くのブロックチェーン設計において重要な設計上の選択肢として、暗号学(cryptography)と暗号経済学(cryptoeconomics)の比較がある。これは(例えばRollupにおいて)有効性証明(つまりZK-SNARKs)と詐欺証明(fraud proofs)の二者択一に帰着することが多い。
ZK-SNARKsは技術的に複雑である。ZK-SNARKsの動作原理の基本的なアイデアは一文で説明できるが、実際にある計算を検証するZK-SNARKを実装すると、その計算自体よりもはるかに複雑なプロセスを要する(そのため、EVM向けのZK-SNARK証明はまだ開発中であり、一方でEVM向けの詐欺証明はすでにテスト段階にある)。効率的なZK-SNARK証明の実装には、特殊目的向けに最適化された回路設計、馴染みのないプログラミング言語の使用、その他多くの課題が含まれる。一方、詐欺証明自体は非常にシンプルである:誰かが異議を唱えたら、単にチェーン上でその計算を再実行するだけ。効率向上のために二分探索スキームを追加することもあるが、それでも大きな複雑性は増えない。
ZK-SNARKsは複雑だが、その複雑性はカプセル化された複雑性である。一方、詐欺証明の比較的低い複雑性は体系的複雑性である。以下は、詐欺証明によって導入される体系的複雑性の例である:
-
検証者のジレンマを回避するために、注意深いインセンティブ設計が必要となる。
-
合意形成の中で完了される場合、詐欺証明用の特別なトランザクスタイプを追加する必要があり、また多数の参加者が同時に詐欺証明を提出しようとした場合の処理も考慮しなければならない。
-
同期ネットワークに依存する。
-
検閲攻撃(censorship attacks)が盗難に悪用される可能性がある。
-
詐欺証明ベースのRollupでは、即時出金を支援するために流動性提供者が求められる。
これらの理由から、複雑性の観点から見ても、ZK-SNARKsに基づく純粋な暗号解法の方が長期的には安全である可能性が高い。ZK-SNARKsは確かに複雑な部分があり、それを選ぶ人々にとっては考慮すべき負担となる。しかし、ZK-SNARKsは「宙に浮いた警告」が少なく、それは全員にとっての利点となる。
その他の例
-
PoW(ナカモトコンセンサス):メカニズムが非常にシンプルで理解しやすいため、カプセル化された複雑性は低いが、利己的マイニング攻撃などにより体系的複雑性は高くなる。
-
ハッシュ関数:カプセル化された複雑性は高いが、性質が非常に明快であるため、体系的複雑性は非常に低い。
-
シャッフルアルゴリズム:内部的に複雑なアルゴリズム(例:Whisk)は強いランダム性を保証し理解しやすいが、内部がシンプルなものは弱いまたは解析困難なランダム性(=体系的複雑性)を生む可能性がある。
-
MEV(マイナー価値抽出):複雑なトランザクションをサポートできるほど強力なプロトコルは内部的にシンプルでも、そのようなトランザクションがブロック提案を極端に歪める形で行われるため、プロトコルのインセンティブ構造に複雑な体系的影響を与える可能性がある。
-
Verkle木:Verkle木には確かにカプセル化された複雑性がある。実際、通常のMerkleハッシュ木よりもはるかに複雑である。しかし、体系的には、キー・バリュー(key-value)マップとまったく同じ、明快でシンプルなインターフェースを提供する。主要な「漏れ」(leak)は、攻撃者が特定の値に対して非常に長い枝(branch)を持つようにVerkle木を操作する可能性だが、これはMerkle木でも同様のリスクが存在する。
どのようにトレードオフすれば良いか?
通常、カプセル化された複雑性が低い選択肢は、体系的複雑性も低い。したがって、明らかにシンプルな選択肢が存在する。しかし、時には一方の複雑性と他方の複雑性の間で難しい選択を迫られることもある。ここで明確になってほしいのは、カプセル化された複雑性の方が危険性は低いということだ。体系的複雑性がもたらすリスクは、仕様の長さの単純な関数ではない。仕様内で10行の小さなコード片が他の部分と相互作用する方が、100行の関数をブラックボックスとして扱うよりもはるかに複雑になり得る。
しかし、カプセル化された複雑性を好むこのアプローチにも限界がある。コードのどこにでもソフトウェアバグは発生し得る。コードが大きくなるにつれて、エラーの発生確率は1に近づいていく。また、時にサブシステムと予期しない新たな方法で相互作用する必要が生じると、当初カプセル化されていたはずの複雑性が、体系的複雑性へと変質してしまうこともある。
後者の一例が、現在のイーサリアムにおける二層状態木(two-level state tree)である。これは、各アカウントオブジェクトがさらに独自のストレージ木を持つという、アカウントオブジェクトの木構造によって特徴付けられる。
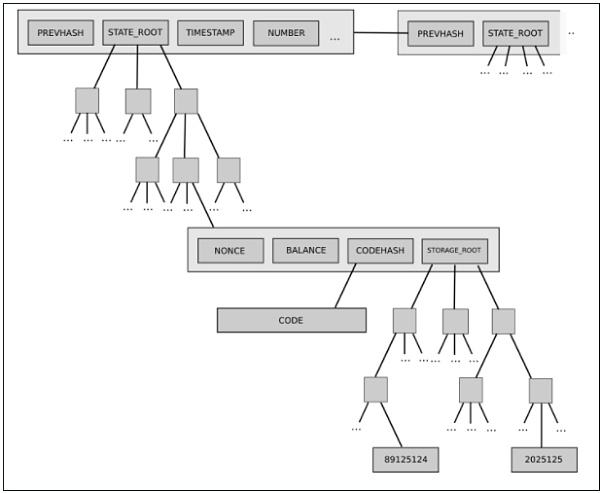
この木構造は複雑だが、当初はその複雑性はうまくカプセル化されているように思えた。プロトコルの他の部分は、読み書き可能なキー/バリュー格納域として木と相互作用するため、木の構造自体については気にする必要がない。
しかし後に、この複雑性が体系的影響を持つことが判明した。アカウントが任意に大きなストレージ木を持つ能力ゆえに、特定の状態領域(例:「0x1234で始まるすべてのアカウント」)が予測可能なサイズを持つことを信頼できなくなる。これにより、状態を複数の部分に分割することが困難になり、同期プロトコルの設計や、ストレージプロセスの分散化の試みがより複雑になってしまう。なぜカプセル化された複雑性が体系的になったのか? インターフェースが変わったからである。解決策は何か? 現在Verkle木への移行案には、バランスの取れた単層木設計への移行も含まれている。
結局のところ、特定の状況においてどちらの複雑性が望ましいかは、簡単な答えのない問題である。我々ができることは、カプセル化された複雑性を適度に支持しつつ、あまり極端にならず、それぞれのケースで判断力を働かせることだけである。場合によっては、カプセル化された複雑性を大きく削減するために、わずかな体系的複雑性を犠牲にするのが最善の場合もある。また、時には「カプセル化されている」と考えていたものが実はそうではなかったと誤判断することもある。ケースバイケースで異なるのだ。
TechFlow公式コミュニティへようこそ
Telegram購読グループ:https://t.me/TechFlowDaily
Twitter公式アカウント:https://x.com/TechFlowPost
Twitter英語アカウント:https://x.com/BlockFlow_News
















