
Vitalik:楕円曲線ペアリングを探求する
TechFlow厳選深潮セレクト

Vitalik:楕円曲線ペアリングを探求する
楕円曲線は30年以上にわたり、暗号化やデジタル署名などの暗号技術の分野で広く使用されてきた。
執筆:Vitalik Buterin
掲載日:2017年1月14日
決定性しきい値署名(deterministic threshold signature)やzk-SNARKs、および他の種類のより単純なゼロ知識証明など、暗号技術における多くの基盤的構成要素の背後にある重要な原初モデルの一つが「楕円曲線ペアリング」である。楕円曲線は30年以上にわたり暗号化やデジタル署名などの暗号応用で広く使われてきたが、「楕円曲線ペアリング」(あるいは双線形写像)はその上に新たに登場した技術であり、暗号学的な乗算を導入することで、楕円曲線に基づくプロトコルが実現可能なことを大幅に拡張している。この記事では、楕円曲線ペアリングについて詳しく紹介し、それがどのように機能するかを簡単に説明する。
この概念は本当に理解しにくいものなので、一回読んだだけ、あるいは十回読んでも完全に理解できるとは期待していませんが、この記事を通じて少なくともいくつかの核心的な洞察を得られることを願っています。
そもそも楕円曲線自体が非常に理解しにくいテーマですが、この記事では読者がその基本的な動作原理についてある程度知っていることを前提としています。もしまだ基本的な知識がない場合は、まずこちらの記事をおすすめします。
要するに、楕円曲線は「点(points)」と呼ばれる数学的対象(具体的には二次元平面上の(x, y)座標を持つ点)と、それらに対して定義された特別な加減算の公式(たとえばR = P + Qの計算)を扱うものである。また、点に整数を乗算することも可能である(たとえばP * n = P + P + … + P)。ただし、nが非常に大きい場合でも効率的に計算する高速アルゴリズムが存在する。
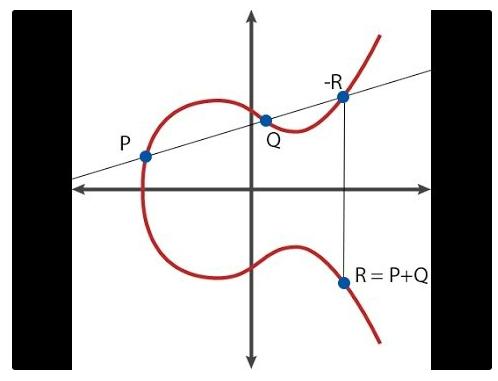
これは点の加算を図示したものです
さらに、「無限遠点(O)」という特別な点があり、これは点演算における零元として機能し、すべての点Pに対してP + O = Pが成り立つ。また、各曲線には「位数(order)」という特性があり、すべての点Pに対してP * n = Oとなるような正整数nが存在する(もちろんP * (n + 1) = P、P * ((7*n) + 5) = P * 5などが成り立つ)。そして、事前に合意された「生成点(generator point)G」があり、これは加法の単位元として、すなわち数字1を表す点として選ばれている。理論的には曲線上の任意の点を生成元にできるが、重要なのはGが統一的に選ばれることである。
ペアリングはさらに複雑な等式を検証できるようにする。たとえば、P = G * p、Q = G * q、R = G * rとしたとき、p * q = rが成立するかどうかを、P、Q、Rの座標のみを使って検証できる。これは一見すると、楕円曲線の基本的なセキュリティ保証が破られているように見える。なぜなら、Pの座標からpの値が漏洩するように思えるからである。しかし実際には、このリスクは非常に限定的である。正確には、決定性Diffie-Hellman問題は容易だが、計算性バージョンは依然として「計算上不可能(computationally infeasible)」である。少なくとも、その難しさは通常の方法でpを求めるのと同程度である。
ペアリングを理解する第三の方法は、おそらく私たちが議論するほとんどの用途において最も直感的なものである。つまり、楕円曲線上の点を単方向暗号関数と見なす(encrypt(p) = p * G = P)とき、従来の楕円曲線の数学は変数間の線形制約を検証できることを意味する(たとえばP = G * p、Q = G * q、R = G * rのとき、5 * P + 7 * Q = 11 * Rを検証することは、5 * p + 7 * q = 11 * rを検証することに相当する)。一方、楕円曲線ペアリングは変数間の二次制約を検証できるようにする(e(P, Q) * e(G, G * 5) = 1を検証することは、p * q + 5 = 0を検証することに相当する)。この二次制約の能力により、決定性しきい値署名やQAP(quadratic arithmetic programs、一種のゼロ知識証明)といった興味深い応用が可能になる。
ここで問題となるのは、先ほど登場したe(P, Q)という演算子が実際には何であるかということである。これがまさに「ペアリング」である。数学者はこれを「双線形写像」と呼ぶこともある。「双線形」とは、以下の条件を満たすことを意味する:
e(P, Q + R) = e(P, Q) * e(P, R)
e(P + S, Q) = e(P, Q) * e(S, Q)
ここで+と*は任意の演算子であり得ることに注意されたい。新しい数学的対象を構築する際、抽象代数では+や*が「どのように定義されるか」よりも、通常の演算と整合的であればよい。たとえばa + b = b + a、(a * b) * c = a * (b * c)、(a * c) + (b * c) = (a + b) * cといった性質が成り立つことである。
もしP、Q、R、Sが単なる数値ならば、ペアリング関数は非常に簡単に構成できる。たとえばe(x, y) = 2^(xy)と定義できる。すると:
e(3, 4 + 5) = 2^(3 * 9) = 2²⁷
e(3, 4) * e(3, 5) = 2^(3 * 4) * 2^(3 * 5) = 2¹² * 2¹⁵ = 2²⁷
確かに双線形性を満たしている!
しかし、このような単純なペアリングは暗号学的には不適切である。なぜなら、整数上で定義された数学的対象を解析するのは非常に簡単だからである。整数の性質により、除算や対数など多くの操作が容易になり、また「公開鍵」や「単方向関数」といった概念もない。さらに、上記のようなペアリングは可逆である:xとe(x, y)の値を知れば、除算と対数を使ってyを計算できる。我々が望む数学的構造は「ブラックボックス」に近いものであり、加減乗除はある程度可能だが、それ以上はできないようなものである。このような状況でこそ、楕円曲線と楕円曲線ペアリングが活躍するのである。
実際に、楕円曲線上の点に対して双線形写像を設計することが可能であることが分かっている。つまり、二つの点PとQを入力として、e(P, Q)という関数をF_p¹²の要素に写像する(少なくとも特定のケースではこれで十分であり、詳細は曲線によって異なるが、後述する)。しかし、その背後にある数学は非常に複雑である。
まず、「素体(prime fields)」と「拡大体(extension fields)」について紹介しよう。上図の曲線は美しいが、それは曲線の方程式が実数上で定義されているという仮定のもとでの話である。もし実際に暗号で実数を使っていたら、対数を使って「逆算」できてしまい、すべてが無意味になってしまうだけでなく、実数を保存するために無限のストレージが必要になるだろう。そのため、代わりに有限体上の数を使う。
素体は0, 1, 2, ..., (p−1)からなる集合で、pは素数であり、以下の演算で定義される:
a + b: (a + b) % p
a * b: (a * b) % p
a - b: (a - b) % p
a / b: (a * b^(p-2)) % p
基本的に、すべての演算はモジュロp(modulo p)で行われる(モジュラー演算についてはこちらに簡単な解説がある)。除算は例外である。一般に3/2は整数ではないが、我々は整数のみを扱いたいので、x * 2 = 3となる整数xを探す。ここで*は前述のモジュラー乗算を意味する。幸いフェルマーの小定理により、指数を使ったこの定義は目的を満たすが、より高速な方法として拡張ユークリッドアルゴリズムがある。p = 7の場合の例を以下に示す:
2 + 3 = 5 % 7 = 5
4 + 6 = 10 % 7 = 3
2 - 5 = -3 % 7 = 4
6 * 3 = 18 % 7 = 4
3 / 2 = (3 * 2^5) % 7 = 5
5 * 2 = 10 % 7 = 3
このような演算を試してみると、一貫しており、通常のすべての規則を満たしていることがわかる。最後の2つの例は(a / b) * b = aを示しており、また(a + b) + c = a + (b + c)、(a + b) * c = a * c + b * cなど、高校で習った代数の等式もすべて成り立つ。実際の楕円曲線では、点と方程式は通常素体上で演算される。
次に、拡大体について説明する。あなたはすでに拡大体の例を見ているかもしれない。数学の教科書で最もよく見る例は複素数体であり、実数体にsqrt(-1) = iという新しい元を追加して拡張したものである。簡単に言えば、拡大体とは既存の体に「新しい元」を「発明」し、その新しい元と既存の元との関係を定義する(上記の例ではi^2 + 1 = 0)。この関係式は既存の数では満たされないものでなければならず、この新しい元を「既存の元のすべての線形結合(linear combination)」の集合に加えることで新しい集合を構成する。
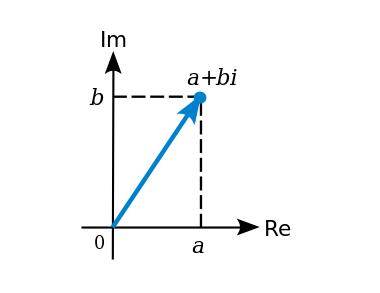
素体に対しても同様に拡張できる。たとえば、mod 7の素体に先ほどのiを追加すると、次のような演算が可能になる:
(2 + 3i) + (4 + 2i) = 6 + 5i
(5 + 2i) + 3 = 1 + 2i
(6 + 2i) * 2 = 5 + 4i
4i * (2 + i) = 3 + i
最後の式は少し理解しにくいかもしれない。まず左辺の乗算を分配律で展開すると4i * 2 + 4i * iとなり、8i - 4となる。mod 7の下ではこれはi + 3となる。除算については:
a / b : (a * b^(p^2-2)) % p
ここではフェルマーの小定理の指数がpからp²に変わっているが、より効率的に計算するにはやはり拡張ユークリッドアルゴリズムが使える。体の任意の元xに対してx ^ (p² − 1) = 1が成り立つため、(p² − 1)を「体の乗法群の位数」と呼ぶ。
実数体に関しては、代数学の基本定理により、その二次拡大体(複素数体)が代数的閉体であることが保証されている。つまり、新たな元jと既存の複素数とのあらゆる多項式関係を満たす元がすでに体内に存在するため、これ以上拡張できない。しかし、素体ではこのような制限はなく、三次拡大(新しい元wが三次多項式を満たし、1, w, w²が線形独立)、高次の拡大、さらには拡大の拡大なども可能である。楕円曲線はまさにこのようなモジュラー演算に基づく複素数上に構築されている。
これらの数学をコードに実装することに興味がある人は、素体および拡大体を実装した例を参照されたい。
再び楕円曲線ペアリングに戻ろう。ここで議論するペアリングはその一種にすぎないが、基本的な考え方は共通している。楕円曲線ペアリングとはG2 × G1 → Gtの写像であり、以下のように定義される:
- G1はy² = x³ + bという形の方程式を満たす楕円曲線であり、点のx, y座標はF_pの元である(つまり普通の数だが、算術演算はある素数を法として行われる)。
- G2も同じ曲線を満たす楕円曲線だが、G2の点のx, y座標はF_p¹²の元である(先ほど説明した「複素数」のようなもの。12次の多項式w¹² − 18w⁶ + 82 = 0を満たす「魔法の数」wを定義する)。
- Gtは楕円曲線演算の結果となる集合である。ここで議論している曲線では、GtはF_p¹²(G2と同じ「複素数」)である。
主に満たすべき性質は双線形性であり、この文脈では次のように表される:
e(P, Q + R) = e(P, Q) * e(P, R)
e(P + Q, R) = e(P, R) * e(Q, R)
(注:厳密にはこれは「整数上の双線形性(bilinearity over ℤ)」であり、ここで扱う楕円曲線上の点は整数点であり、乗算・加算の定義が整数演算後にモジュロを取るものであるため、自然に線形性の一部が満たされる)
ペアリング関数を選択する際の重要な基準は二つある:
- 計算が十分に効率的であること(たとえばすべての点に対して離散対数を取り、それを掛け合わせるという単純なペアリング方法が考えられるが、これは楕円曲線暗号を破るのと同じくらい困難なので、実用的ではない)
- 非退化であること(もちろんe(P, Q) = 1と定義すれば双線形だが、これは特に有用ではない)
では、どうやってこれを実現するのか?
ペアリング関数の背後にある数学は非常に難しく、これまで見てきた以上の高度な代数が必要になるが、概要を説明しよう。まず、「因子(divisor)」という概念を定義する必要がある。これは本質的に、楕円曲線上の点に作用する関数を表現する別の方法である。関数の因子は、その関数がいくつの零点を持ち、どこで無限大になるかを計算する。もう少し理解しやすくするために、いくつかの例を見てみよう。点P = (P_x, P_y)を選び、次の関数を考える:
f(x, y) = x − P_x
その因子は[P] + [−P] − 2 * [O]である(ここで角括弧は点そのものではなく、関数の零点や無限大点の集合における出現を表す;[P] + [Q]と[P + Q]は異なる)。理由は以下の通り:
- x = P_xのときx − P_x = 0となるため、Pで関数はゼロになる
- −PはPと同じx座標を持つため、−Pでもゼロになる
- xが無限大に向かうとき関数も無限大になるため、Oで無限大になるとみなす。この無限遠点は2回カウントされるため、Oに係数−2がつく(負号は無限大点であることを示し、2は2回カウントされることを示す)。
計算的な理由としては、曲線の方程式x³ = y² + bより、xが増加するときyはおおよそxの1.5乗の速さで増加する必要がある。したがって、xのみを含む線形関数では無限大での重みは2だが、yを含む場合は3となる。
次に、直線の関数を考える:
ax + by + c = 0
ここでa, b, cは点PとQを通るように選ばれる。楕円曲線加算の仕組みにより、この直線は必ず−P−Qも通る。xとyの両方に依存して無限大に向かうため、因子は[P] + [Q] + [−P−Q] − 3 * [O]となる。
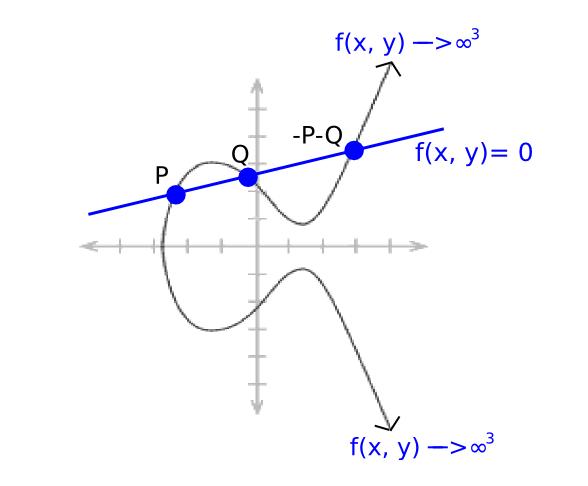
「有理関数」(点の座標に対して有限回の加減乗除で定義される関数)は、定数倍を除いて因子と一対一に対応することが知られている(つまり、二つの関数FとGが同じ因子を持つならば、ある定数kが存在してF = G * kが成り立つ)。
任意の二つの関数FとGに対して、(F * G)の因子はFとGの因子の和に等しい(数学の教科書では(F * G) = (F) + (G)と書かれる)。たとえばf(x, y) = P_x − xならば、(f³) = 3 * [P] + 3 * [−P] − 6 * [O]となる。Pと−Pが3回カウントされるのは、特定の数学的意味でf³が「3倍早く」ゼロに近づくためである。
ある定理によれば、因子の角括弧を取り除き、点を演算した結果が必ずOになる(たとえば[P] + [Q] + [−P−Q] − 3 * [O]を計算するとP + Q − P − Q − 3 * O = O)。この性質を持つ因子は、ある関数の因子になっている。
ここでTateペアリングを見てみよう。以下の因子で定義される関数を考える:
- (F_P) = n * [P] − n * [O]。ここでnはG1の位数であり、すべてのPに対してn * P = Oが成り立つ。
- (F_Q) = n * [Q] − n * [O]
- (g) = [P + Q] − [P] − [Q] + [O]
ここで、積F_P * F_Q * g^nを考える。その因子は:
n * [P] − n * [O] + n * [Q] − n * [O] + n * [P + Q] − n * [P] − n * [Q] + n * [O]
整理すると:
n * [P + Q] − n * [O]
これはF_PやF_Qの因子の形と一致する。したがって、F_P * F_Q * g^n = F_(P + Q)が成り立つ。
ここで「最終指数化(final exponentiation)」と呼ばれる操作を行う。すなわち、前の結果(F_P, F_Qなど)をz = (p¹² − 1) / n乗する。ここでp¹² − 1はF_p¹²の乗法群の位数(つまりすべてのx ∈ F_p¹²に対してx^(p¹² − 1) = 1が成り立つ)。この指数をn乗の結果に適用すると、(p¹² − 1)乗となり、結果は1になる。したがって、最終指数化の後、g^nは消え、F_P^z * F_Q^z = F_(P + Q)^zが得られる。これにより、双線形性の一部が実現される。
さらに二つの引数に対して双線形な関数を構築するには、より高度な数学が必要であり、F_Pだけでなくその因子の計算も行う必要がある。完全なTateペアリングを得るには、さらに「線形同値(linear equivalence)」やWeilの相互法則などの概念を理解する必要がある。詳細はこちらおよびこちらを参照。
実際には、Tateペアリングの改良版──Optimal Ate Pairingが実装されている。このコードではミラーのアルゴリズムを使ってF_pを計算している。
実際、このようなペアリングの使用は刃物の両刃のようなものである。一方でさまざまなプロトコルを実現できるが、他方で使用する楕円曲線の選択には特に注意が必要である。
すべての楕円曲線には「埋め込み次数(embedding degree)」という値があり、これはp^k − 1がnの倍数となる最小の整数kである(pは体の素数、nは曲線の位数)。前述の体ではk = 12であり、従来の楕円曲線暗号(ペアリングを考慮しない)では、埋め込み次数が非常に大きく、ペアリングの計算が計算上不可能になるように設計されている。しかし、注意しないとk = 4やk = 1の体を構成してしまう可能性がある。
k = 1の場合、楕円曲線上の「離散対数問題」(P = G * pからpを求める問題、つまり秘密鍵を割り出す問題)がF_p上の比較的簡単な問題に帰着してしまう(この手法はMOV攻撃と呼ばれる)。埋め込み次数が12以上であれば、このような帰着は不可能か、または帰着後の問題が通常の方法と同等の困難さを持つことが保証される。現在、すべての標準的な曲線パラメータはこの問題の影響を受けないよう厳密に検査されている。
TechFlow公式コミュニティへようこそ
Telegram購読グループ:https://t.me/TechFlowDaily
Twitter公式アカウント:https://x.com/TechFlowPost
Twitter英語アカウント:https://x.com/BlockFlow_News
















