Brakedown:FOAKSにおける多項式コミットメントプロトコルを一文で理解する
TechFlow厳選深潮セレクト
Brakedown:FOAKSにおける多項式コミットメントプロトコルを一文で理解する
もし暗号学者がテンソル積と多項式評価値の間の関係を発見していなかったならば、多項式コミットメントプロトコルBrakedownは生まれにくかっただろうし、Brakedownに基づくOrionやFOAKの誕生も不可能であった。
執筆:Fox Tech CEO 康水躍、Fox Tech 最高科学責任者 孟鉉済
序文:もし暗号学者がテンソル積(Tensor Product)と多項式の評価値との関係性を発見していなければ、多項式コミットメントプロトコル Brakedown は登場しなかったでしょうし、Brakedown を基にした Orion や FOAKS といったまったく新しい高速アルゴリズムも生まれなかったことでしょう。
多くの多項式コミットメントに基づくゼロ知識証明システムでは、異なるコミットメントプロトコルが使用されています。a16z の Justin Thaler が2022年8月に発表した「Measuring SNARK performance: Frontends, backends, and the future」によると、Brakedown は証明サイズが大きいものの、現時点において最も高速な多項式コミットメントプロトコルであると言えます。
FRI、KZG、Bulletproof はより一般的な多項式コミットメントプロトコルですが、その速度はボトルネックとなっています。zkSync が採用する Plonky、Polygon zkEVM が採用する Plonky 2、Scroll が採用する Ultra-Plonk などのアルゴリズムはいずれも KZG ベースの多項式コミットメントに依存しています。Prover 側では多数の FFT 計算および MSM 演算が必要となり、多項式とコミットメントの生成に大きな計算負荷がかかります。MSM は並列処理による高速化の可能性を持ちますが、大量のメモリを消費し、高い並列度でも遅くなる傾向があります。一方、大規模な FFT は実行時のデータ頻繁なシャッフルに強く依存しており、分散環境での複数コンピュータクラスタに跨る高速化は困難です。
こうした計算の複雑さが大幅に低減できたのは、より高速な多項式コミットメントプロトコル Brakedown が存在したからこそです。
FOAKS(Fast Objective Argument of Knowledges)は、Fox Tech が提案した Brakedown ベースのゼロ知識証明フレームワークです。FOAKS は Orion の基礎の上にさらに FFT 演算を削減し、最終的には FFT を完全に排除することを目指しています。また、FOAKS は証明サイズの削減のために非常に巧妙な新しい再帰的証明方式を設計しています。FOAKS フレームワークの利点は、線形時間での証明生成を実現しつつ、比較的小さな証明サイズを持つことであり、zkRollup のようなシナリオに非常に適しています。
以下では、FOAKS が採用する多項式コミットメントプロトコル Brakedown について詳しく説明します。
暗号学におけるコミットメント(Commitment)プロトコルとは、証明者(Prover)がある秘密値に対してコミットメントを行い、公開可能なコミットメント値を生成するものです。このコミットメント値は束縛性(Binding)と秘匿性(Hiding)という性質を持ちます。その後、コミッターはこのコミットメントを開示し、メッセージを検証者に送信することで、コミットメントとメッセージの対応関係を検証します。この点において、コミットメントプロトコルはハッシュ関数と多くの共通点を持ちますが、通常は公開鍵暗号の数学的構造に依存しています。多項式コミットメント(Polynomial Commitment)とは、多項式に対するコミットメントスキームであり、つまりコミットされる値が多項式であるということです。さらに多項式コミットメントプロトコルには、特定の点での評価値を提示し、その正当性を証明するアルゴリズムが含まれており、そのため多項式コミットメント自体が重要な暗号プロトコルとして、多くのゼロ知識証明システムの核となる要素となっています。
最新の暗号学研究では、テンソル積(Tensor Product)と多項式の評価値との関係性が発見されたことで、これに関連する一連の多項式コミットメントプロトコルが誕生しました。Brakedown はその代表的なプロトコルです。
Brakedown の詳細に入る前に、いくつかの基本知識を理解しておく必要があります。線形符号(Linear Code)、衝突耐性ハッシュ関数(Hash Function)、マerkle木(Merkle Tree)、テンソル積(Tensor Product)の演算、および多項式評価値のテンソル積表現について把握する必要があります。
まず、線形符号(Linear Code)についてです。メッセージ長が k、符号語長が n の線形符号とは、Fn 内の線形部分空間 C ⊆ Fn であり、メッセージから符号語への単射(エンコーディング)EC: Fk → C が存在します。任意の符号語の線形結合もまた符号語となります。2つの符号語 u, v の距離とは、それらのハミング距離 Δ(u, v) を指します。
最短距離は d = minu,v Δ(u, v) で表され、このような符号を [n, k, d] 線形符号と呼び、d/n を符号の相対距離とします。
次に、衝突耐性ハッシュ関数(Hash Function)と Merkle木(Merkle Tree)についてです。
H: {0, 1}2λ → {0, 1}λ をハッシュ関数とします。Merkle木は特殊なデータ構造であり、2d 個のメッセージに対するコミットメントを生成し、一つのハッシュ値 h を出力します。任意のメッセージを開示する際には、d+1 個のハッシュ値が必要です。
Merkle木は深さ d の二分木として表現でき、L 個のメッセージ要素 m1, m2, ..., mL がそれぞれ木の葉に対応します。木の各内部ノードは、その2つの子ノードのハッシュ値から計算されます。メッセージ mi を開示する際には、mi から根ノードまでのパスを公開する必要があります。
以下の記法を使用します:
-
h ← Merkle.Commit(m1, ..., mL)
-
(mi, πi) ← Merkle.Open(m, i)
-
{0, 1} ← Merkle.Verify(πi, mi, h)
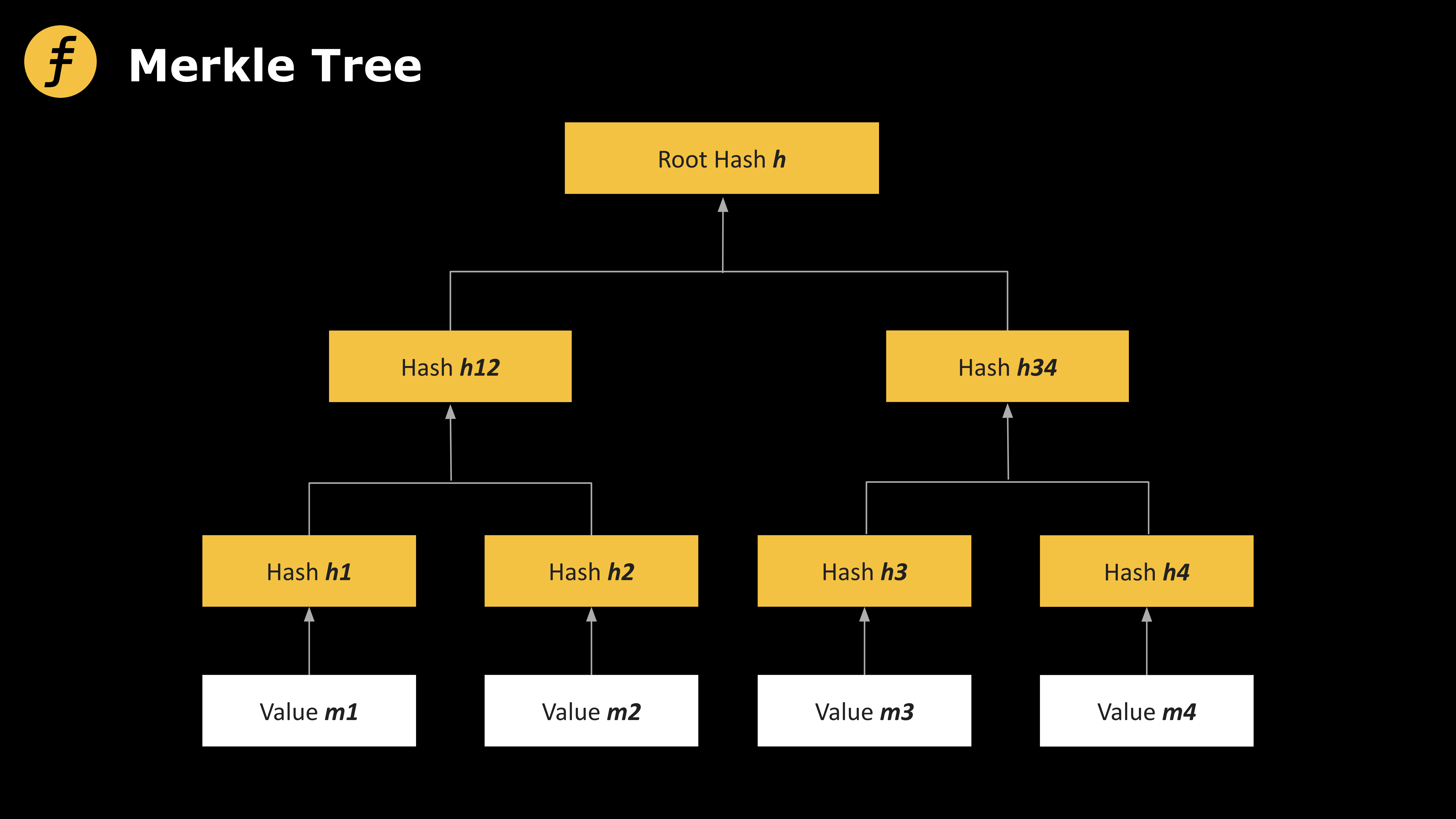
図1:Merkle木(Merkle Tree)
次に、テンソル積(Tensor Product)の演算方法を理解する必要があります。数学的に言えば、テンソルはベクトルや行列を高次元空間へ拡張したものであり、非常に重要な研究対象ですが、本稿ではその詳細な議論は割愛し、ベクトルと行列のテンソル積の計算に焦点を当てます。
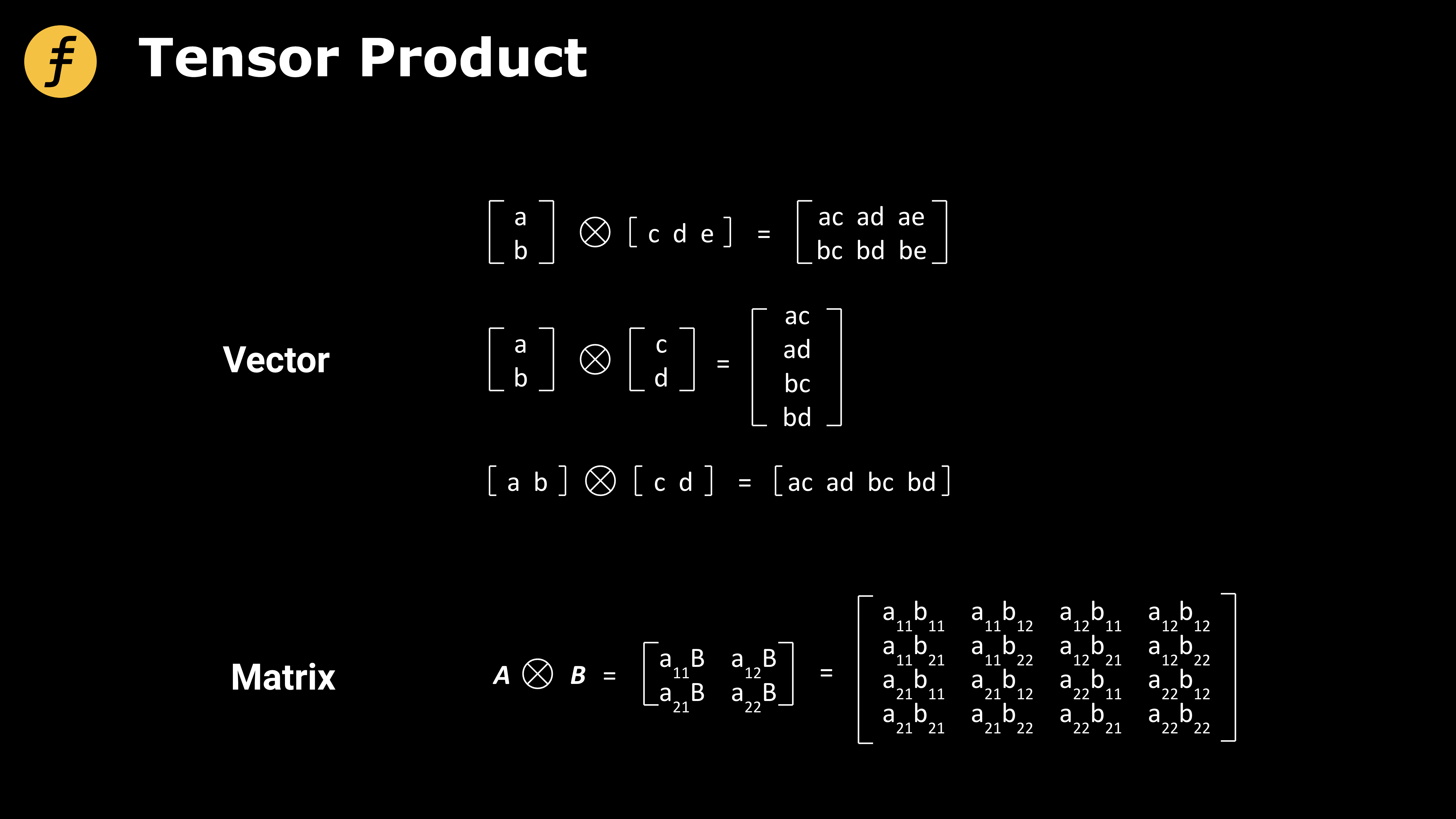
図2:ベクトルと行列のテンソル積演算
続いて、多項式評価値のテンソル積表現について理解します。
[GLS+]では、多項式の評価値はテンソル積の形式で表現可能であると述べています。ここでは、多線形多項式のコミットメントを考えます。
具体的には、ある多項式がベクトル x0, x1, ..., xlogN-1 での評価値は以下のように書けます:
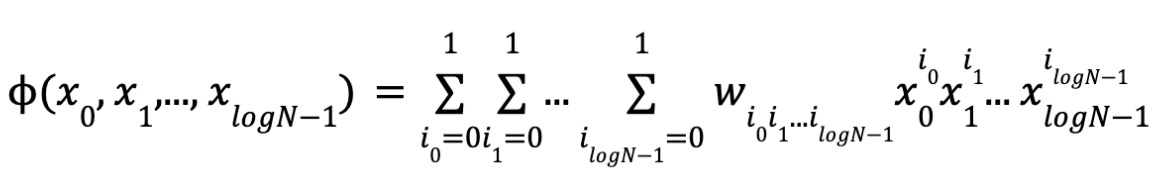
多線形の定義により、各変数の次数は0または1なので、N個の単項式と係数、そして logN 個の変数があります。ここで
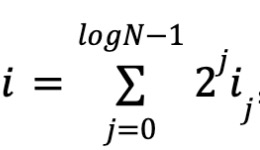
ただし、i0i1...ilogN-1 は i の2進表現です。w を多項式の係数ベクトルとします。
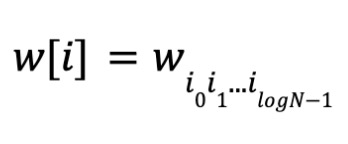
同様に
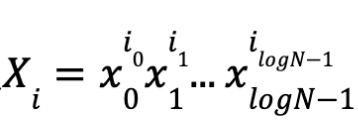
と定義します。そして
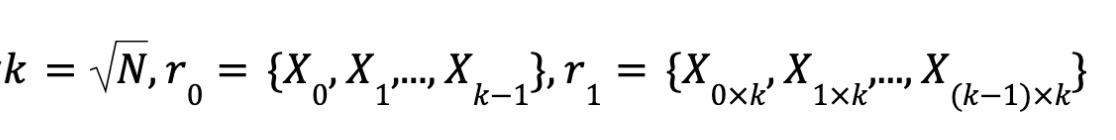
とすると、X = r0 ⊗ r1 が成り立ちます。
したがって、多項式の評価値はテンソル積の形式で表せます:ϕ(x0, x1, ..., xlogN-1) = ⟨w, r0 ⊗ r1⟩。
最後に、FOAKS および Orion[XZS 22] で使用される Brakedown のプロセスを見ていきます。
まず、PC.Commit では、多項式の係数 w を k×k 行列の形に分割し、線形符号で符号化(「予備知識」参照)し、C2 と記述します。次に、C2 の各列 C2[:, i] に対して Merkle木を構築し、各列の Merkle木のルートからさらに別の Merkle木を構築し、最終的なコミットメントとします。
評価値の証明計算では、2つの点を証明する必要があります。すなわち、「近接性(Proximity)」と「一貫性(Consistency)」です。近接性は、コミットされた行列が実際に符号化された符号語と十分に近いことを保証します。一貫性は y = ⟨w, r0 ⊗ r1⟩ であることを保証します。
近接性検査:近接性検査は2段階で行われます。まず、検証者がランダムなベクトル Y0 を証明者に送信します。証明者は Y0 と C1 の内積を計算し、Y0 の各成分を係数として C1 の各行の線形結合を計算します。線形符号の性質により、CY0 は YY0 の符号語となります。次に、証明者は CY0 がコミットされた符号語から実際に計算されたことを証明します。これを証明するために、検証者はランダムに t 列を選択し、証明者は対応する列を開示し、Merkle木の証明を提供します。検証者は、これらの列と Y0 の内積が CY0 の対応する位置と一致するかを確認します。[BCG 20]では、使用する線形符号が一定の相対距離を持つ場合、コミットされた行列は圧倒的確率で何らかの符号語に近接することが証明されています(「圧倒的確率」とは、命題の否定が成立する確率が無視できるほど小さいことを意味します)。
一貫性検査:一貫性検査の手順は近接性検査とほぼ同じですが、ランダムベクトル Y0 の代わりに直接 r0 を線形結合に使用します。同様に、c1 はメッセージ y1 の線形符号であり、ϕ(x) = ⟨y1, r1⟩ が成り立ちます。[BCG 20]では、一貫性検査を通じて、コミットされた行列が符号語に近ければ、圧倒的確率で y = ϕ(x) が成立することが証明されています。
擬似コード形式で、Brakedown プロトコルの流れを示します:
Public input:評価点 X。これはテンソル積 X = r0 ⊗ r1 として解釈される。
Private input:多項式 ϕ。その係数を w で表す。
C を [n, k, d]-線形符号、EC: Fk → Fn を符号化関数、N = k×k とする。N が完全平方でない場合は、次の完全平方までパディングする。行列 mat の i 番目の列を選択するため、Python 風の記法 mat[:, i] を使用する。
-
function PC. Commit(ϕ):
-
w を k×k 行列として解釈する。証明者はローカルでテンソル符号の符号化 C1、C2 を計算する。C1 は k×n 行列、C2 は n×n 行列。
-
for i ∈ [n] do
-
Merkle木のルート Rooti = Merkle.Commit(C2[:, i]) を計算
-
Merkle木のルート R = Merkle.Commit([Root0, ..., Rootn-1]) を計算し、R をコミットメントとして出力
-
function PC. Prover(ϕ, X, R)
-
証明者は検証者からランダムベクトル Y0 ∈ Fk を受信
-
近接性(Proximity)
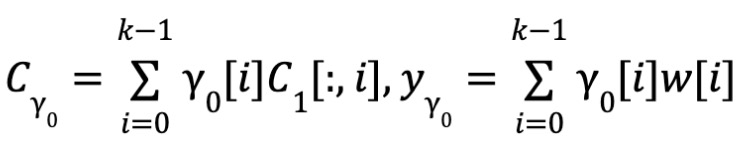
-
一貫性(Consistency)
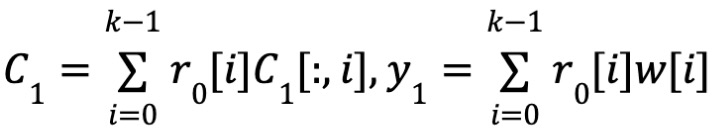
-
証明者は C1, y1, C0, y0 を検証者に送信
-
検証者は t 個のインデックスを [n] からランダムに選択し、配列 Î として証明者に送信
-
for idx ∈ Î do
-
証明者は C1[:, idx] および R 下での C2[:, idx] に対する Rootidx の Merkle木証明を検証者に送信
-
function PC. VERIFY_EVAL(πX, X, y=ϕ(X), R)
-
近接性:∀idx ∈ Î, CY0[idx] == ⟨Y0, C1[:, idx]⟩ かつ EC(YY0) == CY0
-
一貫性:∀idx ∈ Î, C1[idx] == ⟨Y0, C1[:, idx]⟩ かつ EC(Y1) == C1
-
y == ⟨r1, y1⟩
-
∀idx ∈ Î, EC(C1[:, idx]) が Rootidx と一致し、Rootidx の Merkle木証明が有効であること
-
上記すべての条件が満たされれば受理。そうでなければ拒否。
結び:多項式コミットメントは非常に重要な暗号プロトコルであり、多くの暗号システム、特にゼロ知識証明システムで広く利用されています。本稿では、多項式コミットメントプロトコル Brakedown 及び関連する数学的知識について詳細に紹介しました。FOAKS の重要な基盤コンポーネントとして、Brakedown は FOAKS の実装性能向上に大きく寄与しています。
参考文献
-
[GLS+]: Alexander Golovnev, Jonathan Lee, Srinath Setty, Justin Thaler, Riad S. Wahby. Brakedown: Linear-time and post-quantum snarks for r 1 cs. Cryptology ePrint Archive. https://ia.cr/2021/1043.
-
[XZS 22]: Xie T, Zhang Y, Song D. Orion: Zero knowledge proof with linear prover time[C]//Advances in Cryptology–CRYPTO 2022: 42nd Annual International Cryptology Conference, CRYPTO 2022, Santa Barbara, CA, USA, August 15–18, 2022, Proceedings, Part IV. Cham: Springer Nature Switzerland, 2022: 299-328. https://eprint.iacr.org/2022/1010
-
[BCG 20]: Bootle, Jonathan, Alessandro Chiesa, Jens Groth. "Linear-time arguments with sublinear verification from tensor codes." Theory of Cryptography: 18th International Conference, TCC 2020, Durham, NC, USA, November 16–19, 2020, Proceedings, Part II 18. Springer International Publishing, 2020.
-
a16z crypto の Justin Thaler, Measuring SNARK performance: Frontends, backends, and the future https://a16z crypto.com/measuring-snark-performance-frontends-backends-and-the-future/
-
テンソル積の紹介:https://blog.csdn.net/chenxy_bwave/article/details/127288938
TechFlow公式コミュニティへようこそ
Telegram購読グループ:https://t.me/TechFlowDaily
Twitter公式アカウント:https://x.com/TechFlowPost
Twitter英語アカウント:https://x.com/BlockFlow_News