
Le club de blockchain de Stanford : La loi de Moore s'applique aussi aux preuves à divulgation nulle, dont la génération double chaque année en nombre par seconde
TechFlow SélectionTechFlow Sélection

Le club de blockchain de Stanford : La loi de Moore s'applique aussi aux preuves à divulgation nulle, dont la génération double chaque année en nombre par seconde
Dans les prochaines années, le nombre de preuves générées par seconde doublera avant de croître progressivement en s'approchant des gains sous-jacents du calcul universel.
Rédaction : STANFORD BLOCKCHAIN CLUB, ROY LU
Traduction : TechFlow
Note : Cet article provient de Stanford Blockchain Review. TechFlow est partenaire officiel de Stanford Blockchain Review et a l'autorisation exclusive de traduire et republier cet article.

Introduction
Dans cet article, nous explorerons comment les preuves à connaissance nulle (ZK) peuvent transformer notre vie au-delà du Web3. J’aborderai les leviers de performance, proposerai une « loi de Moore des ZK » et identifierai les modèles d’accumulation de valeur.
Les preuves à connaissance nulle comptent parmi les technologies les plus transformatrices du Web3 actuel, avec un potentiel énorme en matière d’évolutivité, d’authentification et de confidentialité. Toutefois, les performances actuelles limitent leur déploiement dans de nombreux cas d’usage potentiels. À mesure que la technologie ZK mûrira, je pense qu’elle connaîtra une croissance exponentielle et s’appliquera largement tant dans le Web3 que dans les secteurs traditionnels. De même que la loi de Moore prévoit un doublement tous les deux ans de la densité des transistors sur une puce, je propose ici une loi exponentielle similaire pour les preuves à connaissance nulle, ainsi formulée :
Dans les années à venir, le nombre de preuves générées par seconde doublera ou plus, puis tendra asymptotiquement vers les gains du calcul universel sous-jacent.
Aperçu de la loi de Moore
La loi de Moore, formulée en 1965 par Gordon Moore, cofondateur d'Intel, prédit que « la complexité des circuits intégrés électroniques à semi-conducteurs doublera tous les deux ans ». Pendant les 58 dernières années, cette loi a propulsé l'informatique mobile, l'apprentissage automatique, et presque tous les aspects de notre vie numérique, transformant ainsi notre interaction avec la technologie.
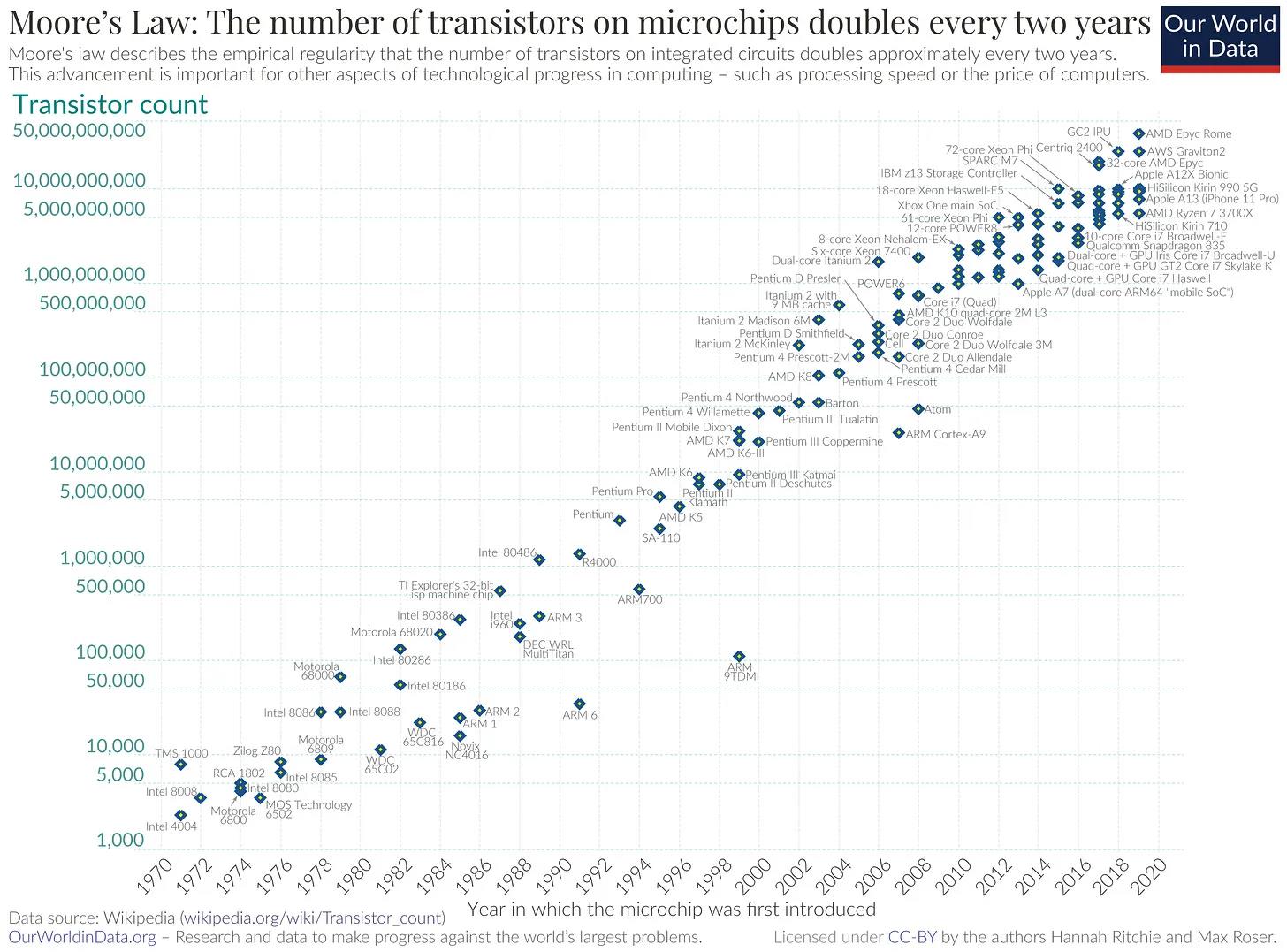
Gordon Moore a observé empiriquement que, tandis que le nombre de transistors sur une puce doublait, le coût de fabrication restait globalement stable grâce aux économies d'échelle. Il a également noté que la demande croissante en puissance de calcul inciterait à investir davantage pour augmenter la densité des transistors.
À mesure que la puissance de calcul augmentait de manière exponentielle sur des puces toujours plus petites, cette évolution quantitative s’est traduite par des changements qualitatifs dans notre utilisation et notre interaction avec les ordinateurs.
Nos téléphones sont aujourd’hui des ordinateurs plus puissants que celui utilisé lors de la mission Apollo 11, logés commodément dans nos poches, nous permettant de diffuser en continu du contenu depuis n’importe quel site web et de communiquer avec n’importe qui dans le monde. L’entraînement des grands modèles linguistiques a permis la sortie de ChatGPT, transformant notre interaction avec l’information, du simple accès aux données à une synthèse intelligente.
L’essor des preuves à connaissance nulle et du Web3
Tout comme le doublement du nombre de transistors et la loi de Moore ont entraîné une transformation qualitative de notre interaction avec la technologie moderne, la croissance exponentielle des preuves à connaissance nulle ouvrira la voie à une nouvelle vague d’applications. Fondamentalement, les ZK confèrent confidentialité, exactitude et évolutivité — des propriétés ancrées dans le calcul privé, la vérifiabilité et la concision récursive propres aux ZK. Ces caractéristiques représentent un changement fondamental vers un nouveau paradigme de calcul.
Calcul privé
Les preuves à connaissance nulle permettent d’effectuer des calculs sur des modules privés, tout en ne partageant et en validant extérieurement que les résultats. Prenons un exemple concret : si une banque utilisait le calcul ZK, elle pourrait prévenir le vol d’identité. Par exemple, un utilisateur pourrait autoriser un programme d’approbation de prêt à exécuter des opérations sur ses informations d’identité et son historique de crédit afin d’obtenir une approbation, sans avoir à divulguer ses données sensibles — la confidentialité étant ainsi préservée. Dans le Web3, les ZK alimentent des réseaux L1 entièrement privés (comme Aleo et Mina), ou des réseaux de paiement privés (comme Zcash, zk.money, Elusiv et Nocturne). Les ZKP permettent également à des projets comme Renegade de gérer des dark pools, en affichant des ordres de transaction sans influencer les prix du marché. La valeur peut être transférée sans révéler les données personnelles des utilisateurs.
Exactitude vérifiable
Pour des calculs opaques, les ZK fournissent une traçabilité des entrées, sorties et processus de calcul. Un exemple est l’apprentissage machine décentralisé, rendu possible par un réseau de nœuds de calcul distants, démocratisant ainsi l’intelligence artificielle. Les ZKP peuvent prouver les données, les poids et le nombre de cycles d’entraînement en apprentissage automatique, et attester que l’ensemble du processus s’est déroulé conformément aux attentes — l’exactitude est ainsi établie. Dans le Web3, des équipes comme Gensyn et Modulus Labs ont commencé à mettre en œuvre le zkML, tandis que des machines virtuelles ZK générales comme Risc Zero sont en développement. Pour prouver l’exactitude des états inter-chaînes, les ZKP sont utilisés dans des ponts ZK tels que Polymer, Succinct Labs, Herodotus et Lagrange. Les ZK permettent également à des applications comme Proven de prouver l’exactitude de leurs réserves.
Concision récursive
Les ZK permettent aussi de combiner plusieurs preuves en une seule. Un autre exemple concret est le suivi d’authenticité dans une chaîne d’approvisionnement. Chaque fabricant, à chaque étape de la chaîne, peut utiliser des ZKP pour prouver l’authenticité de son produit sans divulguer d’informations sensibles sur sa fabrication. Ces ZKP peuvent ensuite être combinés de manière récursive, produisant une preuve finale attestant de la justesse de toute la chaîne — assurant ainsi l’évolutivité. Dans le Web3, des milliers de transactions peuvent être regroupées en une seule preuve, alimentant des réseaux L2 comme Starkware, Scroll et zkSync, augmentant considérablement le débit des blockchains.
Définir la loi de Moore des preuves à connaissance nulle
À partir de ce qui précède, nous avons vu l’analogie entre l’explosion d’applications rendue possible par les transistors et celle que les ZKP déclenchent dans l’innovation Web3. Il est maintenant temps de formuler précisément une « loi de Moore des ZK », en comparant le calcul universel et le calcul à connaissance nulle.
Calcul universel et calcul à connaissance nulle
Dans le calcul universel, les portes logiques sont constituées de transistors à base de silicium-oxyde-métal. Chaque porte appartient à l’un des opérateurs tels que ET, OU, XOR, etc. Ensemble, ces opérateurs permettent l’exécution des programmes.
Toutes choses égales par ailleurs, le calcul ZK est plus coûteux que le calcul universel. Par exemple, « hacher 10 Ko avec SHA2 via Groth16 prend 140 secondes, alors que sans ZK cela prend quelques millisecondes ». Cela s’explique par le fait que le calcul ZK utilise des opérations arithmétiques complexes pour chaque opérateur.
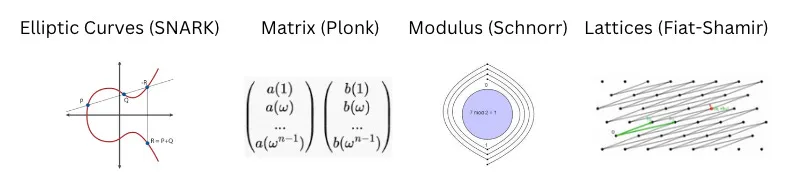
Dans le calcul ZK, les opérateurs peuvent être exprimés dans des corps finis. Dans le cas des SNARKs, chaque opérateur est calculé sur une courbe elliptique. Dans d'autres variantes de ZK, les opérateurs peuvent être composés de matrices, de treillis ou de groupes modulaires — des structures mathématiques complexes qui effectuent elles aussi des opérations arithmétiques. Effectuer des additions, soustractions ou multiplications simples avec ces opérateurs est très coûteux. Les données d’entrée sont converties en éléments de corps finis, plutôt qu’en nombres classiques. Cette complexité structurelle est la base de la sécurité offerte par la cryptographie. Bien que les détails arithmétiques dépassent le cadre de cet article, l’essentiel est que, tout comme les portes logiques s’exécutent sur des circuits physiques, les logiques ZK s’exécutent dans des circuits logiciels.
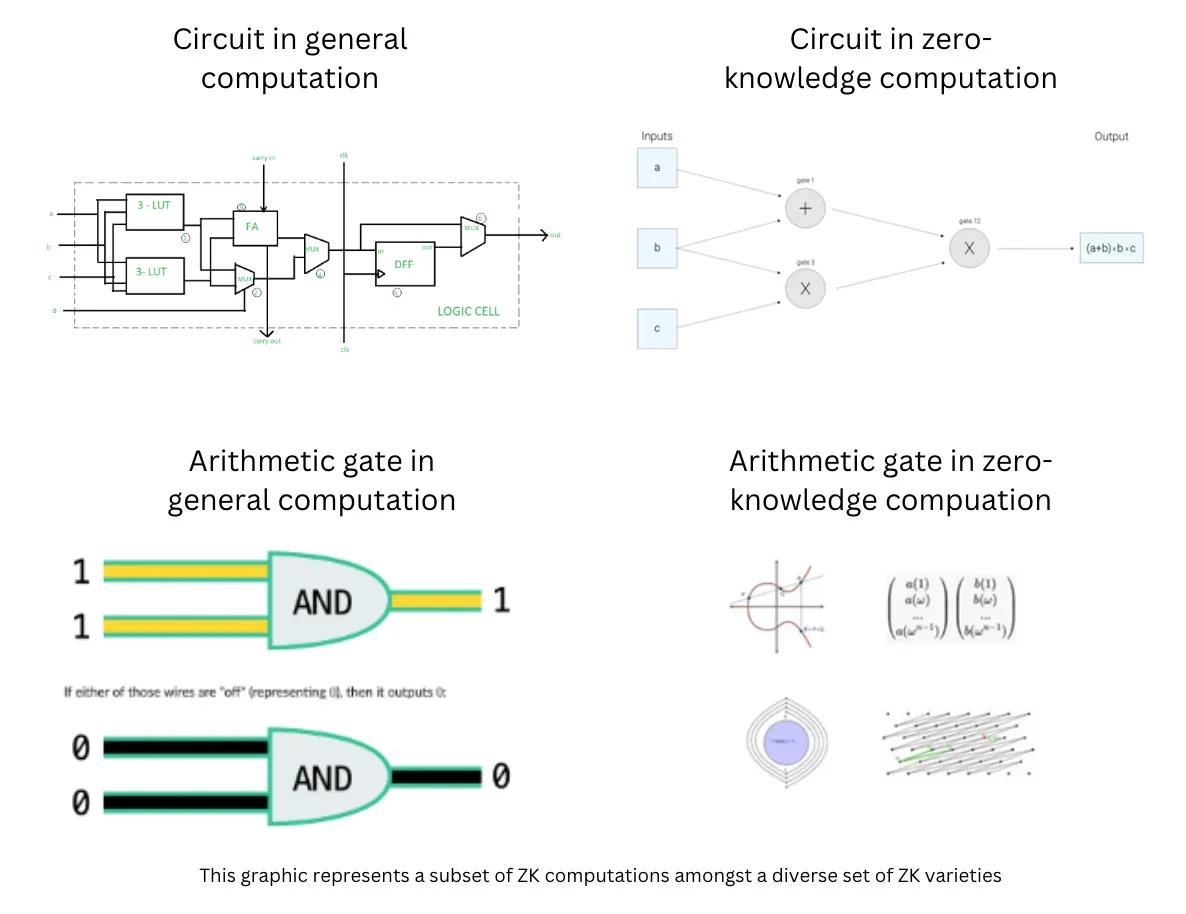
Ainsi, dans le calcul universel, les gains de performance sont régit par les lois physiques, tandis que dans le calcul ZK, ils sont régit par les lois mathématiques. Nous comprenons donc que, bien que l’accélération matérielle apporte des gains significatifs, appliquer la loi de Moore aux ZK relève principalement du domaine logiciel, plutôt que matériel. Sur la base de ces principes fondamentaux, nous pouvons maintenant esquisser à quoi ressemblerait une loi de Moore spécifique aux ZK.
Les améliorations majeures en ZK sont discontinues
Peut-être l’observation la plus importante est que, contrairement aux améliorations continues du calcul universel, celles du calcul ZK se produisent par sauts discontinus.
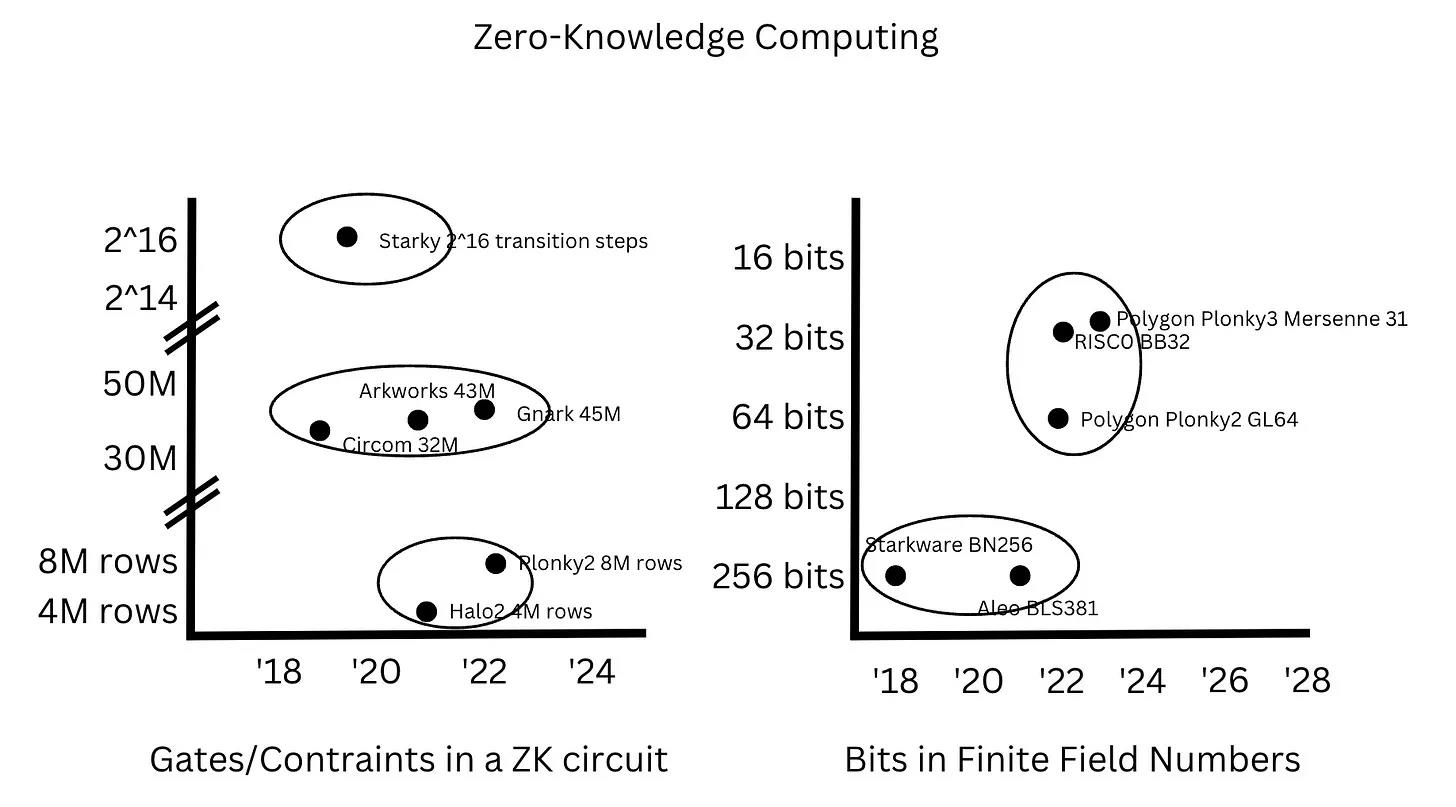
En effet, entre 2005 et 2020, le nombre de cœurs CPU a doublé environ tous les cinq ans, tout comme la fréquence d’horloge a grossièrement doublé entre les années 1990 et 2010. En revanche, le nombre de contraintes dans les circuits ZK n’a pas évolué continûment, mais a connu des sauts : passant des 30-40 millions de contraintes des SNARKs aux 4-8 millions de lignes des PLONKs, puis aux 2^14-2^16 étapes de transition des STARKs. De même, le nombre de bits dans les corps finis est resté autour de 256 bits entre 2018 et 2022, puis a chuté à 32 bits entre 2022 et 2023, afin d’exploiter les registres 32 bits.
De plus, les derniers développements autour de HyperSpartan supportent des systèmes de contraintes personnalisables (CCS), capables de capturer simultanément R1CS, Plonkish et AIR sans surcoût. L’introduction de SuperNova, construit sur Nova — un système de preuve récursive haute vitesse avec schéma de pliage —, est compatible avec différents jeux d’instructions et systèmes de contraintes. Ces deux avancées élargissent encore davantage l’espace de conception des architectures ZK.
Sur la base de ces observations, la loi fondamentale de Moore pour les ZK ne repose pas sur un vecteur d’amélioration continue unique, mais sur des gains globaux de performance — mesurés par le nombre de preuves générées par unité de temps — pilotés par des améliorations discontinues. Je pense que, avant de converger vers les gains du calcul universel sous-jacent, la loi de Moore des ZK connaîtra des sauts révolutionnaires discrets :
Dans les prochaines années, le nombre de preuves générées par seconde doublera ou plus, puis tendra asymptotiquement vers les gains du calcul universel sous-jacent.
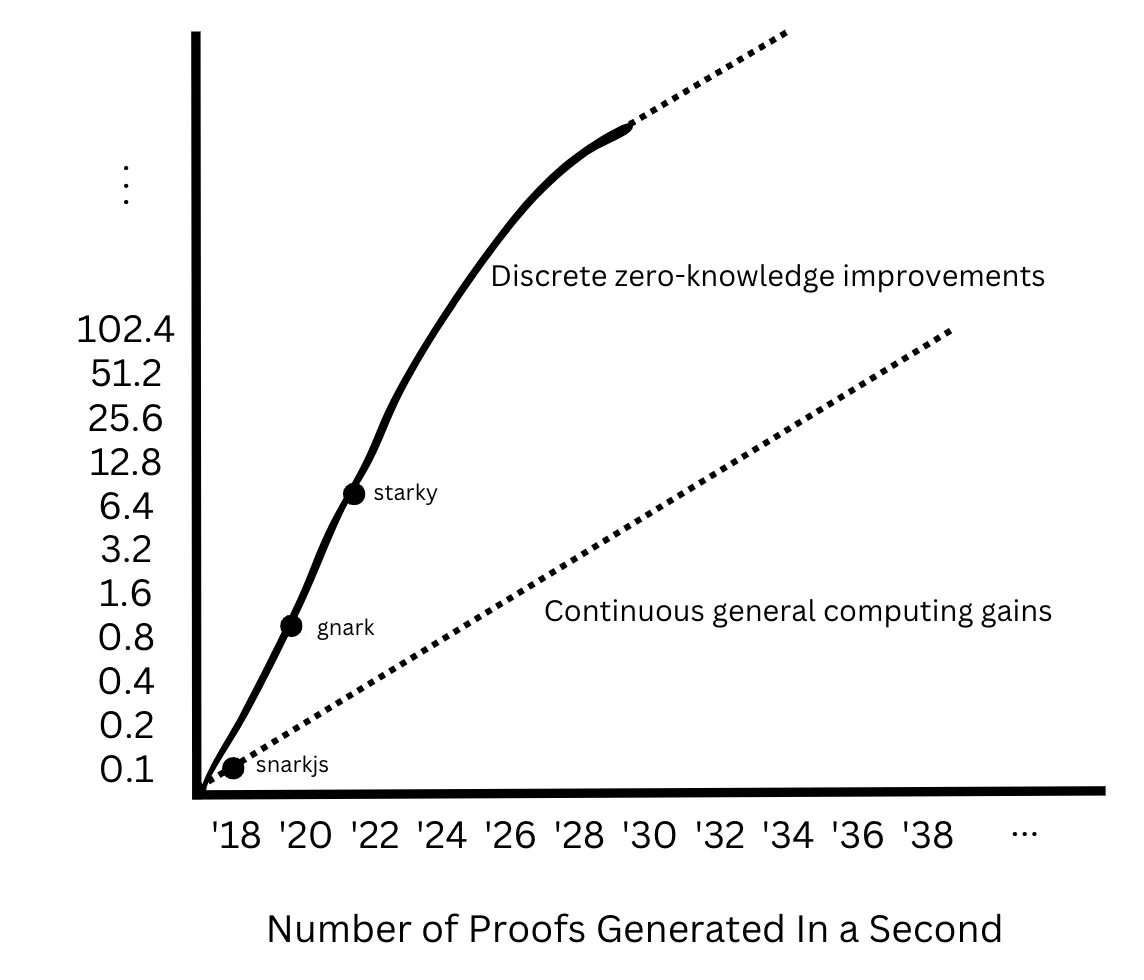
Réduire le coût des preuves à connaissance nulle
Comme mentionné précédemment, les preuves ZK actuelles sont encore trop fragiles et coûteuses pour de nombreuses applications potentielles. En particulier, le coût de vérification dépasse largement celui de la génération. Une estimation approximative indique que générer une preuve coûte moins d’un dollar, basée sur deux faits : 1) sur Amazon AWS, une instance EC2 dotée de 16 cœurs CPU et 32 Go de RAM coûte 0,40 $/heure, et le coût d’un nœud de calcul décentralisé devrait être inférieur ; 2) Polygon Hermez coûte 4 à 6 $/heure et génère environ 20 preuves par heure.
Cependant, le coût de vérification on-chain reste élevé, nécessitant entre 230 000 et 5 millions de gas par vérification, soit environ 100 à 2000 dollars par vérification. Bien que les ZK Rollups bénéficient d’économies d’échelle en répartissant les coûts sur des milliers de transactions, d’autres types d’applications ZK doivent trouver des moyens de réduire le coût de vérification afin de permettre les innovations applicatives mentionnées plus haut, et ainsi améliorer concrètement la qualité de vie des utilisateurs finaux.
Étant donné que les percées en matière de capacité ZK pourraient survenir par sauts discontinus, examinons les domaines où ces percées sont susceptibles d’avoir lieu. Voici quelques axes d’optimisation potentiels listés dans le zkprize :
-
Optimisations algorithmiques, notamment la multiplication scalaire multiple (MSM) et la transformation de théorie des nombres (NTT), fréquemment utilisées pour accélérer la cryptographie sur courbes elliptiques, elles-mêmes pouvant bénéficier d’accélération matérielle. La transformation de Fourier est un exemple de NTT ayant déjà été optimisée dans diverses implémentations.
-
Le traitement parallèle peut augmenter le débit ZK en déléguant certaines parties — prétraitement des structures de données, évaluation du circuit ou génération de preuve — à plusieurs unités de traitement ou threads.
-
Les optimisations de compilateur peuvent améliorer l’allocation des registres, l’optimisation des boucles, la gestion mémoire et la planification des instructions.
En matière d’optimisation algorithmique, citons la transition de l’arithmétisation R1CS des SNARKs vers les formulations Plonkish utilisées dans Halo2, Plonky2 et HyperPlonk, différentes de l’AIR employé dans les preuves Starky. De plus, les récents progrès sur les schémas de pliage sont prometteurs, car HyperNova permet un calcul incrémentallement vérifiable avec des systèmes de contraintes personnalisables. Concernant le traitement parallèle, Plonky2 publié par l’équipe Polygon a élargi les possibilités de génération parallèle de preuves récursives. En matière d’optimisation de compilateur, l’utilisation d’un LLVM adapté aux ZK est particulièrement intéressante, car son IR (représentation intermédiaire) peut être compilé en opcodes indépendants de l’architecture. Par exemple, Nil Foundation avec ZK-LLVM et Risc0 avec leur zkVM utilisent LLVM pour générer des traces exécutant chaque étape en preuve ZK. Des machines virtuelles ZK ou des compilateurs LLVM généralistes étendent les ZK à des cas d’usage hors blockchain et améliorent la portabilité du code pour une plus large communauté de développeurs.
Impacts pour les bâtisseurs ZK
Dans le calcul universel, l’accumulation de valeur bénéficie souvent aux acteurs existants : par exemple, les fabricants de puces tirent parti de fossés protecteurs liés à d’importants investissements en capital, soutenant des améliorations progressives de leurs techniques de fabrication pour produire des puces toujours plus petites. En revanche, comme les innovations en ZK se produisent par sauts révolutionnaires discrets, de nouvelles équipes ont encore de nombreuses opportunités de surpasser les acteurs existants grâce à des percées technologiques issues de la recherche, telles que l’invention de nouveaux systèmes de preuve.
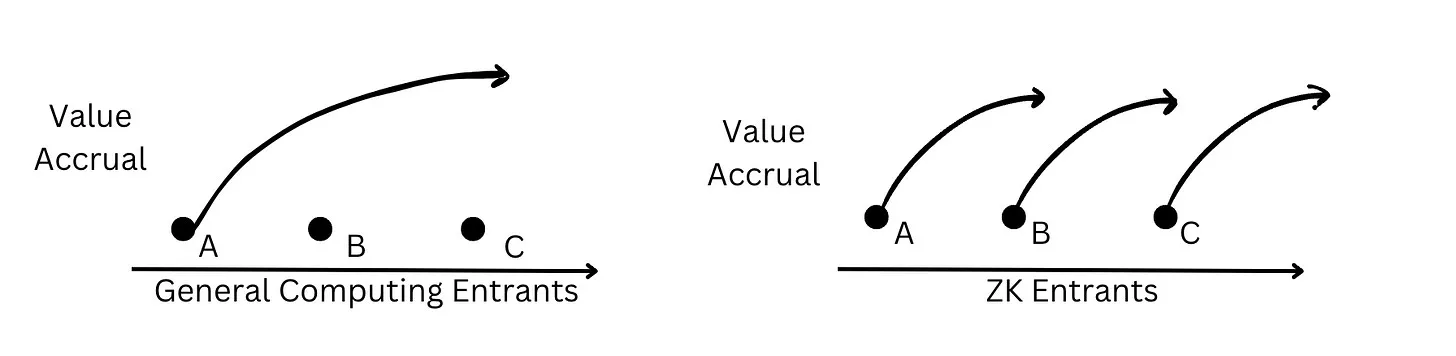
Sur la base de cette théorie, plusieurs enseignements s’imposent pour les bâtisseurs ZK du Web3 :
-
Les bâtisseurs ZK devraient envisager une conception modulaire. Les protocoles impliquant des circuits ZK devraient adopter une architecture modulaire, leur permettant de remplacer facilement les composants par la technologie ZK la plus avancée disponible.
-
Les participants peuvent tirer parti des disruptions portées par la recherche. Pour les équipes disposant de capacités de recherche, il est possible de proposer ou d’implémenter en premier un nouveau système de preuve révolutionnaire, surpassant ainsi les équipes existantes.
-
Les intégrateurs verticaux peuvent tirer profit de la combinaison des dernières technologies. Étant donné que chaque couche de la pile ZK — du matériel au compilateur en passant par les circuits — peut faire l’objet d’améliorations spécifiques, les intégrateurs verticaux peuvent adopter de manière modulaire les dernières avancées et fournir aux équipes applicatives la technologie ZK la plus performante au moindre coût.
Sur la base de ces observations, j’anticipe trois évolutions majeures dans l’industrie :
-
De nouvelles équipes surpasseront les protocoles ZK existants grâce à des percées technologiques.
-
Les protocoles existants chercheront à renforcer leurs avantages concurrentiels via l’écosystème plutôt que via la technologie.
-
Des fournisseurs ZK intégrés verticalement émergeront, offrant les dernières technologies à moindre coût. Innovation et disruption continueront de façonner ce domaine en pleine expansion.
Conclusion
Le paradoxe de la technologie veut que lorsqu'elle fonctionne bien, elle devient invisible. Nous ne pensons pas au verre quand nous buvons de l’eau, tout comme nous ne remarquons pas la puce informatique lorsque nous envoyons un e-mail. Plus un objectif est facile à atteindre, plus nous oublions le processus qui y conduit.
Les preuves à connaissance nulle sont déjà en passe d’offrir des applications évolutives avec une meilleure expérience utilisateur. Quand la technologie fonctionnera parfaitement, nous ne remarquerons plus la présence des preuves, mais constaterons que nos transactions sont plus privées, nos informations plus fiables, et les rollups plus rapides et moins coûteux. Ainsi, les ZK pourraient finalement s’intégrer discrètement aux fondations de notre quotidien, comme l’ont fait les transistors, les microprocesseurs, et désormais l’intelligence artificielle.
Nous n’aurons plus besoin de réfléchir à la manière dont les ZK empêchent la fraude électorale, économisent des coûts de transaction en désintermédiant les systèmes financiers, ou démocratisent l’entraînement de l’IA via le calcul décentralisé ZK. Peut-être qu’un jour, tout comme nous tenons pour acquise l’observation de Moore selon laquelle « le nombre de transistors sur une puce doublera tous les 18 à 24 mois », nous considérerons comme allant de soi que « le nombre de preuves ZK par seconde croît exponentiellement chaque année », tout en profitant paisiblement des fruits de ces innovations. Lorsque l’objectif devient simple à atteindre, plus personne ne vantera les ZK — nous poursuivrons simplement notre vie quotidienne.
Bienvenue dans la communauté officielle TechFlow
Groupe Telegram :https://t.me/TechFlowDaily
Compte Twitter officiel :https://x.com/TechFlowPost
Compte Twitter anglais :https://x.com/BlockFlow_News











