Comment concevoir un schéma de preuve récursif extrêmement élégant ?

2023.02.21

Partager vers

TechFlow SélectionTechFlow Sélection

Comment concevoir un schéma de preuve récursif extrêmement élégant ?

Presque tous les défis rencontrés dans le domaine des zkRollup et des zkEVM sont essentiellement des problèmes algorithmiques. L'accélération matérielle des ZKP est fréquemment mentionnée principalement parce que les algorithmes actuels sont généralement lents.

2023.02.21 - 05:10:14

ZKP

Dédié à des analyses Web3 approfondies

Rédaction : Lin Yanxi, CTO de Fox Tech ; Meng Xuanji, scientifique en chef chez Fox Tech

Préambule : Presque tous les défis rencontrés dans le domaine du zkRollup et du zkEVM sont essentiellement des problèmes algorithmiques. L’accélération matérielle des preuves à connaissance nulle (ZKP) est fréquemment évoquée principalement parce que les algorithmes actuels sont généralement lents. Pour éviter le piège gênant de « compenser un manque d’efficacité algorithmique par du matériel », nous devrions résoudre le problème à la racine, au niveau fondamental de l’algorithme. La conception d’un schéma de preuve récursive extrêmement élégant est la clé pour surmonter ce défi.

Avec le développement continu des contrats intelligents, de plus en plus d’applications web3 voient le jour, entraînant une hausse rapide du volume des transactions sur Ethereum et autres blockchains traditionnelles de couche 1 (Layer1), qui peuvent à tout moment subir des congestions. Il devient donc crucial de trouver comment bénéficier simultanément de la sécurité offerte par la couche 1 tout en atteignant une efficacité accrue.

Concernant Ethereum, le zkRollup utilise des algorithmes de preuve à connaissance nulle comme composant de base afin de déplacer hors chaîne les calculs coûteux autrement exécutés sur la Layer1, puis fournit à la chaîne une preuve attestant de la correction de ces exécutions. Ce secteur regroupe notamment des projets tels que StarkWare, zkSync, Scroll et Fox Tech.

En réalité, les conceptions de zkRollup imposent des exigences élevées en matière d’efficacité : on souhaite que la taille de la preuve soumise soit suffisamment petite afin de réduire la charge de calcul supportée par la Layer1. Pour obtenir des preuves particulièrement courtes, divers projets de zkRollup améliorent continuellement leurs algorithmes et architectures. Par exemple, Fox a intégré les derniers algorithmes de preuve à connaissance nulle pour développer son propre algorithme de preuve, FOAKS, permettant d’optimiser conjointement le temps de génération de la preuve et sa longueur.

Par ailleurs, lors de la phase de vérification des preuves, la méthode la plus simple consiste à générer les preuves linéairement puis à les vérifier séquentiellement. Pour améliorer l’efficacité, une idée naturelle consiste à regrouper plusieurs preuves en une seule, ce qu’on appelle communément l’agrégation de preuves (Proof Aggregation).

Intuitivement, la vérification des preuves générées par un zkEVM constitue un processus linéaire : le vérificateur (Verifier) doit valider chaque preuve individuellement, une après l’autre. Toutefois, cette approche présente une faible efficacité et un coût de communication élevé. Dans le contexte d’un zkRollup, des frais de vérification plus élevés se traduisent directement par davantage de calculs sur la Layer1, entraînant ainsi des frais de gaz (Gas fee) accrus.

Examinons un exemple : Alice souhaite prouver au monde entier qu’elle s’est rendue au parc Fox chaque jour du 1er au 7 du mois. Pour cela, elle pourrait prendre une photo chaque jour, du 1er au 7, dans le parc avec le journal daté du jour correspondant. Ces sept photos, regroupées ensemble, formeraient alors une preuve.

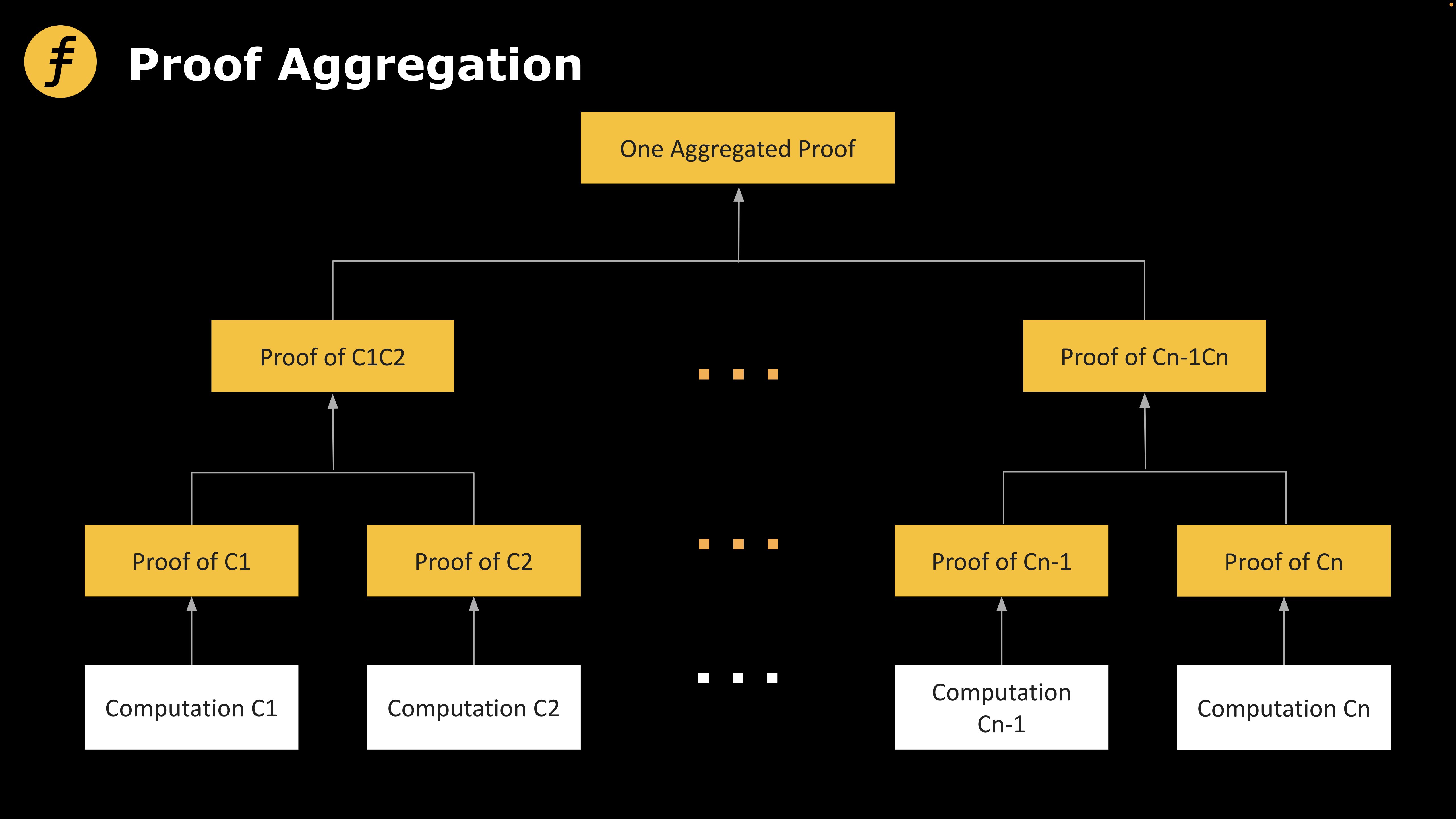
Comment concevoir un schéma de preuve récursive extrêmement élégant ?

Figure 1 : Schéma classique d’agrégation de preuves

Dans cet exemple, placer directement les sept photos dans une enveloppe représente intuitivement l’agrégation de preuves. En pratique, cela correspond à concaténer différentes preuves et à les vérifier linéairement l’une après l’autre : d’abord la première, puis la deuxième, etc. Or, cette méthode ne réduit ni la taille totale de la preuve ni le temps nécessaire à sa vérification ; son effet est identique à celui d’une vérification individuelle et séquentielle. Pour réaliser une compression spatiale de complexité logarithmique, il faut recourir à la technique décrite ci-après : la preuve récursive (Proof Recursion).

Schémas de preuve récursive utilisés par Halo2 et STARK

Pour mieux expliquer ce qu’est une preuve récursive, revenons à notre exemple précédent.

Les sept photos d’Alice constituent en réalité sept preuves distinctes. Imaginons maintenant les combiner : Alice prend une photo le 1er, puis le 2nd elle prend une nouvelle photo en tenant la photo du 1er et le journal du 2nd. Le 3e jour, elle reprend une photo en tenant la photo du 2nd et le journal du 3e jour. Et ainsi de suite, jusqu’au 7e jour où elle prend la dernière photo en tenant celle du 6e jour et le journal du 7e jour. En voyant cette dernière photo, les observateurs peuvent alors vérifier qu’Alice s’est bien rendue au parc chaque jour entre le 1er et le 7e. On constate que les sept preuves initiales ont été compressées en une seule. La technique clé ici repose sur l’idée de « photo contenant une photo », c’est-à-dire imbriquer récursivement chaque photo précédente dans la suivante. Cette approche diffère fondamentalement de la simple prise d’une photo regroupant toutes les autres.

La technique de preuve récursive utilisée dans les zkRollups permet une forte compression de la taille des preuves. Plus précisément, chaque transaction génère une preuve. Notons C0 le circuit de calcul initial de la transaction, P0 la preuve de validité de C0, et V0 le processus de vérification de P0. Le prouveur (Prover) transforme alors V0 lui-même en un circuit équivalent, noté C0’. Ensuite, pour une autre transaction dont le circuit est C1, on peut fusionner les circuits C0’ et C1. Ainsi, une fois que la preuve de validité P1 du circuit combiné est vérifiée, cela revient à avoir simultanément validé les deux transactions — réalisant ainsi une compression.

En réexaminant ce processus, on constate que le principe de compression réside dans la transformation du processus de vérification en un circuit, puis dans la génération d’une « preuve de la preuve ». D’un point de vue conceptuel, cette opération peut être itérée indéfiniment de manière descendante, d’où le terme « preuve récursive ».

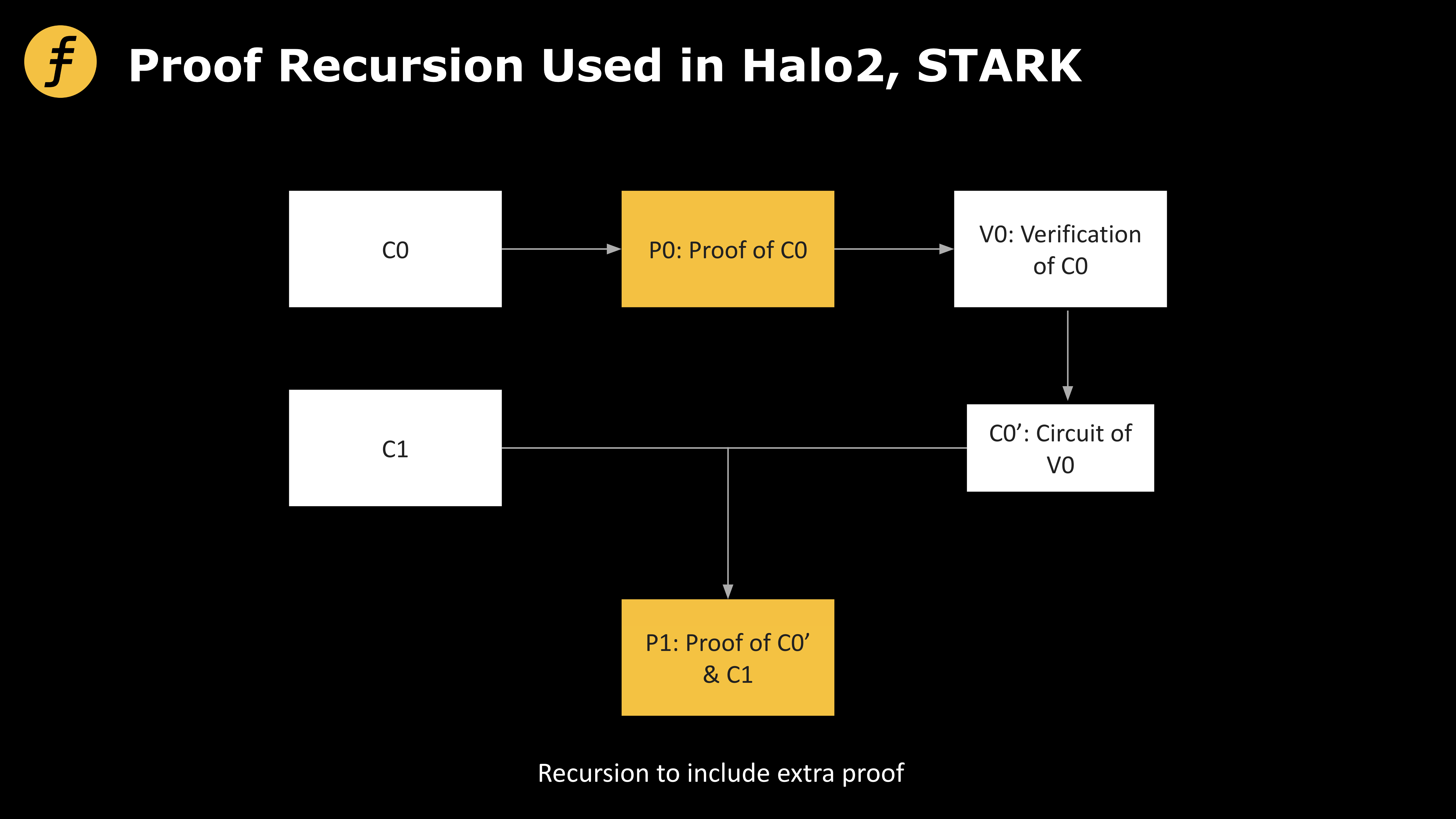
Comment concevoir un schéma de preuve récursive extrêmement élégant ?

Figure 2 : Schéma de preuve récursive utilisé par Halo2 et Stark

Le schéma de Proof Recursion adopté par Halo2 et STARK permet de générer des preuves en parallèle et de les agréger, de sorte que la vérification d’une seule preuve atteste simultanément de la validité de plusieurs transactions. Cela compresse considérablement les coûts de calcul et améliore grandement l’efficacité du système.

Toutefois, cette optimisation reste encore située au niveau des algorithmes spécifiques de preuve à connaissance nulle. Pour aller plus loin, des optimisations et innovations plus fondamentales sont nécessaires. L’algorithme FOAKS développé par Fox applique précisément le concept de récursivité à l’intérieur même d’une preuve unique, permettant ainsi de franchir un nouveau cap.

Schéma de preuve récursive utilisé par FOAKS

Fox Tech est un projet de zkRollup basé sur zkEVM. Son système de preuve utilise également la technique de preuve récursive, mais avec une différence conceptuelle majeure : Fox applique la récursivité à l’intérieur même d’une preuve. Pour illustrer l’idée centrale du schéma de preuve récursive utilisé par Fox — à savoir la réduction progressive du problème à prouver jusqu’à ce qu’il devienne suffisamment simple — examinons un nouvel exemple.

Dans l'exemple précédent, Alice prouve qu’elle s’est rendue au parc Fox en prenant une photo. Bob propose alors une autre idée : prouver qu’Alice est allée au parc peut être ramené à prouver que son téléphone s’y est trouvé. À son tour, prouver que le téléphone s’y est trouvé peut être réduit à prouver que le signal de localisation du téléphone était dans la zone du parc. Ainsi, pour prouver sa présence, Alice n’a qu’à envoyer une géolocalisation depuis son téléphone pendant qu’elle est au parc. La taille de la preuve passe alors d’une photo (donnée de très haute dimension) à une donnée tridimensionnelle (longitude, latitude, heure), réduisant efficacement les coûts. Cet exemple n’est pas parfait — on pourrait objecter que la présence du téléphone n’implique pas nécessairement celle d’Alice — mais dans des cas réels, ce processus de réduction suit rigoureusement des fondements mathématiques.

Plus concrètement, l’utilisation de la récursivité par Fox s’opère au niveau des circuits. Lorsqu’on construit une preuve à connaissance nulle, on commence par exprimer le problème sous forme de circuit, puis on dérive des équations devant être satisfaites par les calculs. Au lieu de simplement montrer que ces équations sont satisfaites, on les reconvertit elles-mêmes en circuits, et ainsi de suite, jusqu’à ce que les équations restantes soient assez simples pour être prouvées directement sans difficulté.

Ce processus illustre clairement une interprétation plus fidèle du terme « récursif ». Il convient de noter que toutes les méthodes ne permettent pas d’appliquer efficacement cette technique. Supposons qu’à chaque étape de récursion, une preuve de complexité O(n) soit transformée en une preuve de complexité O(f(n)), et que le coût de la récursion elle-même soit O(g(n)). Après une itération, la complexité totale devient O₁(n) = O(f(n)) + O(g(n)) ; après deux itérations, O₂(n) = O(f(f(n))) + O(g(n)) + O(g(f(n))) ; après trois itérations, O₃(n) = O(f(f(f(n)))) + O(g(n)) + O(g(f(n))) + O(g(f(f(n)))), etc. Par conséquent, cette technique de récursion n’est bénéfique que si, pour un certain k, on a Oₖ(n) < O(n). C’est exactement ce type de récursion que Fox exploite efficacement pour réduire la complexité des preuves.

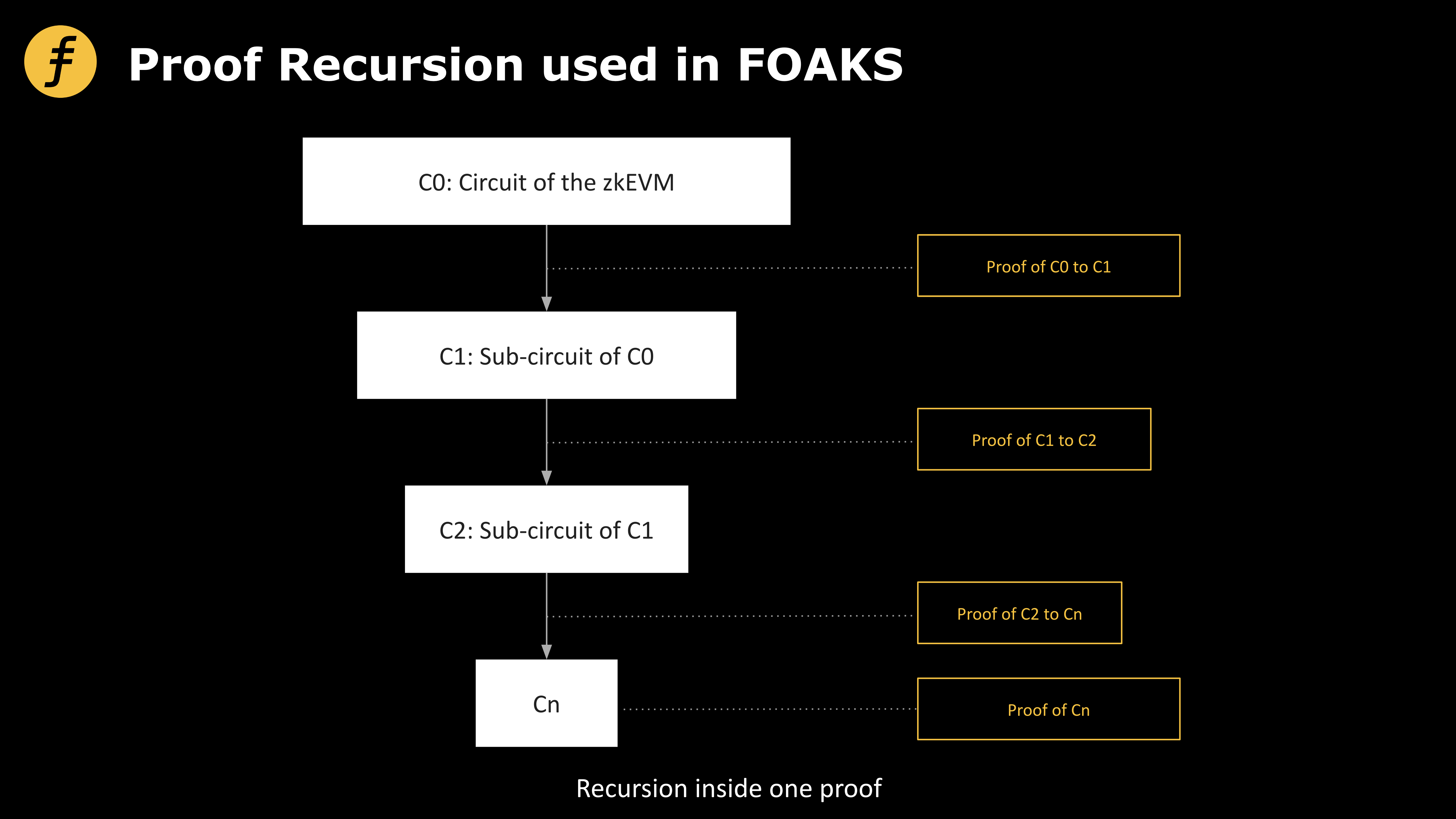
Comment concevoir un schéma de preuve récursive extrêmement élégant ?

Figure 3 : Schéma de preuve récursive utilisé par ZK-FOAKS

Conclusion

La complexité des preuves est depuis toujours l’un des enjeux clés dans les applications des preuves à connaissance nulle. Cette caractéristique devient d’autant plus cruciale que les faits à prouver deviennent complexes. Dans des scénarios massifs comme le zkEVM, la complexité des preuves influence de façon déterminante les performances du produit et l’expérience utilisateur. Parmi les nombreuses méthodes visant à réduire cette complexité finale, l’optimisation de l’algorithme central reste la plus importante. Partant des algorithmes les plus avancés, Fox a conçu un schéma de preuve récursive d’une élégance remarquable, exploitant cette technologie pour créer l’algorithme ZK-FOAKS, particulièrement adapté au zkEVM, et qui pourrait bien devenir un pilier de performance dans le domaine du zkRollup.