Livre blanc sur la conception de la monnaie stable Curve : AMM avec liquidations continues / sans liquidation
TechFlow SélectionTechFlow Sélection

Livre blanc sur la conception de la monnaie stable Curve : AMM avec liquidations continues / sans liquidation
On espère que le mécanisme proposé pourra résoudre les risques liés aux liquidations effectuées dans le but de fabriquer des stablecoins et d'accorder des prêts.
Auteur : JamesX, iZUMi Research
Version bilingue du livre blanc sur la conception de la stablecoin Curve, accompagnée de notes explicatives en chinois pour faciliter la compréhension, ainsi que des corrections d'erreurs typographiques présentes dans l'original. À utiliser comme référence pour l'étude.
Vue d'ensemble
Plusieurs concepts sont essentiels dans cette conception de stablecoin : l'algorithme AMM de prêt-liquidation (LLAMMA), le PegKeeper (mécanisme de stabilisation de la parité) et la politique monétaire. Le point central repose principalement sur LLAMMA : remplacer le processus traditionnel de liquidation dans les systèmes de prêt avec surengagement par un AMM à usage spécifique.
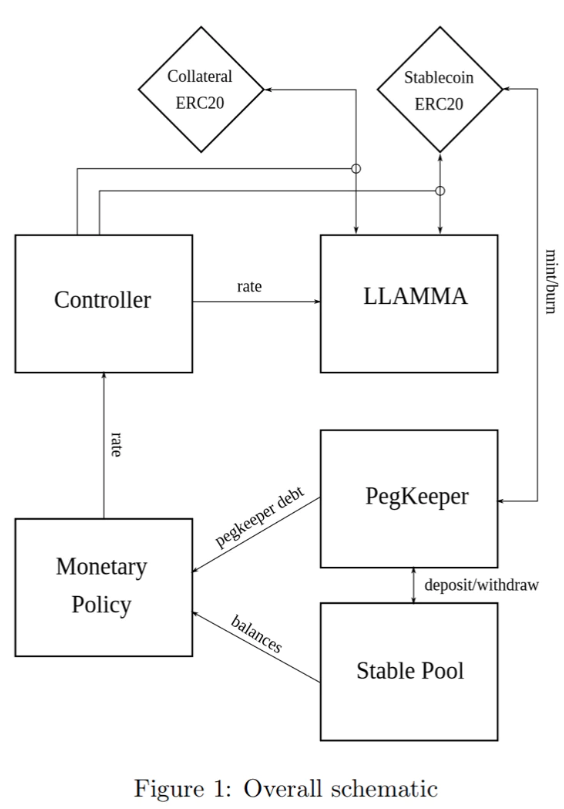
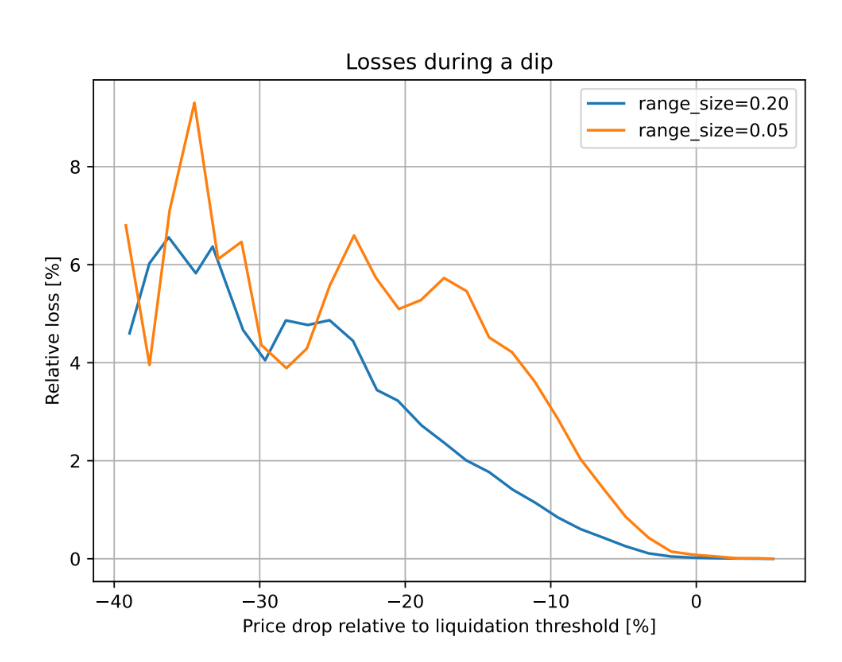
Figure 2 : Dépendance des pertes par rapport aux fluctuations de prix relatives au seuil de liquidation. Fenêtre d’observation de 3 jours.
Dans cette conception, lorsqu’un utilisateur emprunte en déposant une garantie, même si le prix de celle-ci chute puis rebondit après avoir atteint le seuil de liquidation, les pertes restent négligeables.
Par exemple, selon des simulations basées sur les données historiques ETH/USD depuis septembre 2017, si un CDP est laissé sans surveillance pendant 3 jours, et que le prix chute de 10 % sous le prix de liquidation, seulement 1 % de la garantie est perdu.
AMM à liquidation continue / sans liquidation (LLAMMA)
L'idée centrale derrière la conception de cette stablecoin est l'algorithme AMM de prêt-liquidation. L'idée consiste à convertir automatiquement entre la garantie (par exemple, ETH) et la stablecoin (appelée ici USD). Si le prix de la garantie est élevé, le dépôt de l'utilisateur reste entièrement en ETH ; mais lorsque le prix baisse, il se transforme progressivement en USD. Cette approche diffère fondamentalement des AMMs classiques, où les USD sont placés dans la partie supérieure de la courbe AMM et l’ETH dans la partie inférieure.
La description ci-dessous ne constitue pas une preuve rigoureuse et entièrement cohérente. De nombreux éléments (en particulier les invariants) ont été déterminés à partir de considérations multidimensionnelles. Une description mathématique complète pourrait nécessiter davantage de recherches, mais celle fournie ici est jugée suffisante pour permettre une implémentation dans des contrats intelligents.
Ce fonctionnement n’est possible qu’avec une source de prix externe via oracle. En résumé, si l’on prend un AMM classique (par exemple, une courbe de bonding en forme d’hyperbole) et que l’on fait varier son « prix central » de manière croissante ou décroissante, les jetons peuvent être convertis « adiabatiquement » d’USD en ETH (ou inversement), tout en fournissant de la liquidité dans les deux sens durant le processus (voir Figure 3).Cela rappelle vaguement le phénomène de « croisement évité » en physique quantique (aussi appelé transition de Landau-Zener), bien que cela reste uniquement une analogie conceptuelle — la description mathématique du processus pourrait être très différente.

La plage de concentration de liquidité est appelée ici une « bande » (band). Pour une bande donnée définie par un prix d’oracle po, la liquidité s’étend de pcd à pcu. Nous cherchons à ce que pcd(po) et pcu(po) soient des fonctions de po dont la croissance est plus rapide que linéaire, c’est-à-dire qu’elles augmentent plus vite que po (voir Figure 4). Par ailleurs, définissons les prix p↓ et p↑ tels que p↓(po) = po et p↑(po) = po, représentant respectivement les extrémités inférieure et supérieure de la bande dans la limite adiabatique (lorsque p = po).
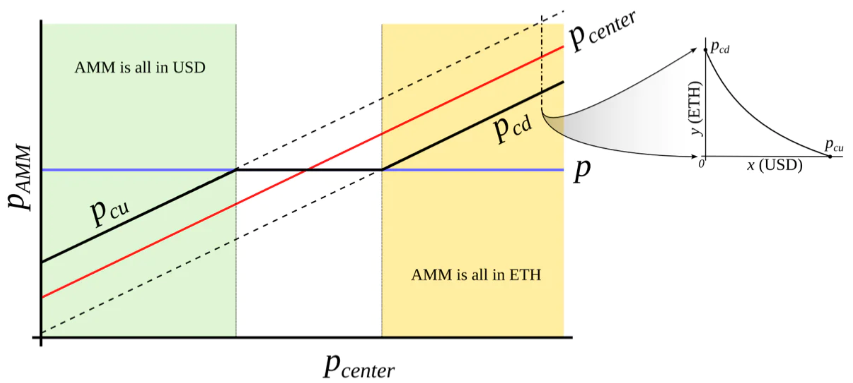
Figure 3 : Comportement d’un « AMM avec source de prix externe ». Le prix externe pcenter détermine la plage autour de laquelle la liquidité est concentrée. L’AMM supporte une liquidité concentrée entre les prix pcd et pcu, avec pcd < pcenter < pcu. Lorsque le prix actuel p sort de l’intervalle [pcd, pcu], l’AMM est soit entièrement en stablecoin (à pcu), soit entièrement en garantie (à pcd). Lorsque pcd ≤ p ≤ pcu, le prix de l’AMM égale le prix actuel p.
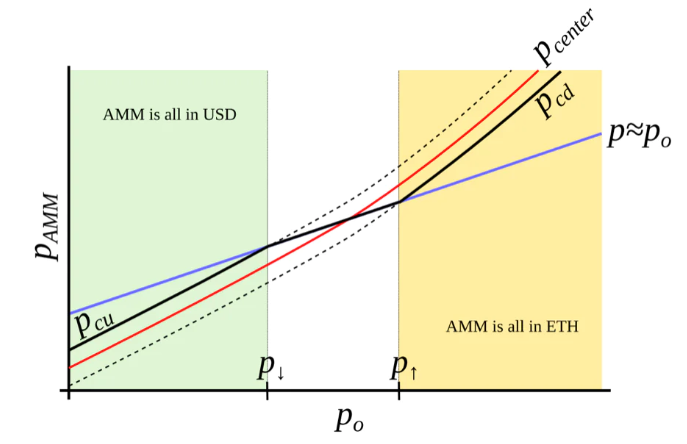
Figure 4 : L’AMM que nous souhaitons construire. Notre objectif est de concevoir un AMM où pcd et pcu sont des fonctions de po qui croissent plus rapidement que po lui-même. Ainsi, lorsque l’ETH est cher, l’AMM sera entièrement converti en ETH, et lorsque l’ETH est bon marché, il sera entièrement converti en USD.
Nous partons d’un modèle similaire à Uniswap V3, en divisant l’espace des prix en bandes, et en conservant la forme hyperbolique de la courbe de bonding grâce à l’ajout de « soldes virtuels ». Soit x la quantité de USD et y celle d’ETH, l’invariant « renforcé » de type produit constant devient alors :

On peut aussi poser x₀ ≡ x + f et y₀ ≡ y + g, ce qui ramène l’invariant à la forme familière I = x₀y₀. Toutefois, f et g ne sont pas constants : ils varient en fonction du prix de l’oracle externe po (et l’invariant I également, donc il n’est invariant que lorsque po est fixe). Pour un po donné, f et g restent constants sur toute la bande. Comme mentionné précédemment, p↑ désigne le prix supérieur de la bande, p↓ le prix inférieur. Nous définissons A (mesurant le degré de concentration de liquidité) comme suit :

La propriété recherchée est la suivante : un prix po plus élevé doit entraîner, à soldes égaux, un prix plus élevé dans l’AMM. Ainsi, le prix de marché actuel (qui suit en moyenne po) serait inférieur à ce prix, poussant la bande à trader vers une composition entièrement en ETH (et vice versa dans l’autre direction). Plusieurs formulations peuvent satisfaire cette condition, mais nous en cherchons une telle que :
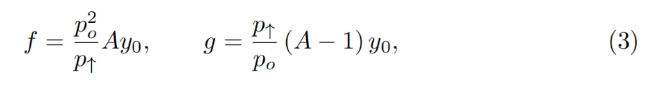
où y₀ est une mesure du dépôt actuel dans la bande exprimée en ETH, définie ainsi : lorsque le prix actuel p, p↑ et po sont égaux, alors y = y₀ et x = 0 (voir le point sur la Figure 4 où po = p↑). En remplaçant y à ce moment-là :

Le prix étant égal à dx₀/dy₀, dans le cas d’un invariant produit constant, on obtient :
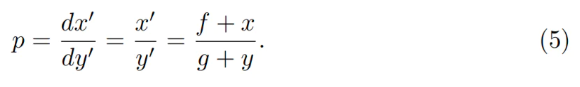
On peut vérifier la cohérence de ces formules en substituant x=0 (pour po=p↑) ou y=0 (pour po=p↓).
Pour une bande donnée, on connaît généralement p↑, donc aussi p↓, po, la constante A, ainsi que x et y (soldes actuels dans la bande). Pour calculer les autres valeurs, il faut d’abord trouver y₀. Celui-ci peut être obtenu en résolvant une équation quadratique issue de l’invariant :
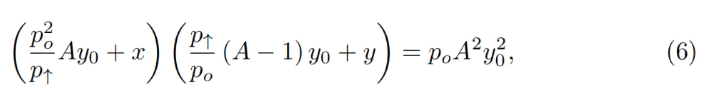
Ce qui devient une équation quadratique en y₀ :
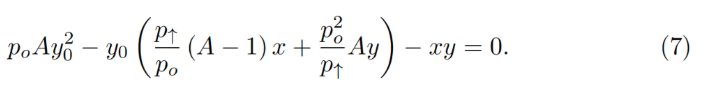
Dans le contrat intelligent, cette équation quadratique est résolue dans la fonction get_y0.
Lorsque le prix de l’oracle po reste constant, l’AMM fonctionne normalement, vendant de l’ETH à la hausse et en rachetant à la baisse. En remplaçant simplement x=0 dans l’équation d’invariant pour obtenir le prix actuel descendant pcd, ou y=0 pour obtenir le prix actuel montant pcu, on peut montrer que le prix de l’AMM, pour les valeurs actuelles de po et p↑, est donné par :
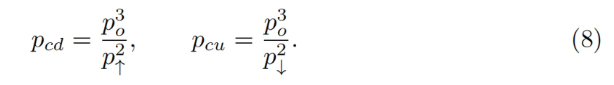
Un autre problème pratique important est le suivant : si le changement de prix est suffisamment lent pour que le prix de l’oracle po suive « adiabatiquement » le marché (sans saut de bande), combien d’ETH final y↑ obtiendra-t-on (si le prix monte) ou combien de USD final x↓ (si le prix baisse), étant donné les soldes initiaux x et y, et en partant de p = po ? Bien que ce ne soit pas un problème mathématique direct, des calculs numériques révèlent une réponse relativement simple :

Ces résultats seront utilisés pour évaluer la sécurité des prêts et les pertes potentielles de l’AMM.
Nous disposons maintenant d’une description complète d’une bande. L’ensemble de l’espace des prix est divisé en bandes adjacentes, où les prix p↓ et p↑ se touchent. En définissant un prix de base pbase et un numéro de bande n, on obtient :
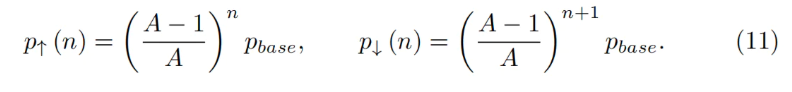
Pour toute bande, on peut démontrer que les solutions des formules 7 et 5 satisfont :
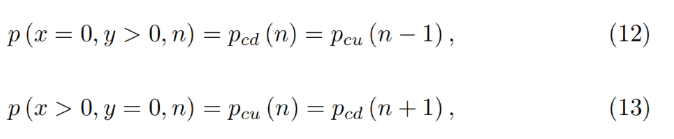
Cela confirme qu’il n’y a aucun espace vide entre les bandes.
Les transactions conservent l’invariant de la formule 1, mais lorsque le prix po change, le prix interne de l’AMM évolue aussi : quand po diminue, le prix interne augmente, et inversement (selon un coefficient cubique), comme indiqué par la formule 8.
LLAMMA vs Stablecoin
Une stablecoin fonctionne comme un CDP : les utilisateurs empruntent une monnaie stable en déposant une garantie volatile (cryptomonnaie, par exemple ETH). La garantie est intégrée dans la plage de prix de LLAMMA (dans une bande). Si le prix de la garantie baisse lentement, l’ETH est progressivement converti en stablecoin suffisant pour couvrir le remboursement du CDP (ce qui peut se produire via une auto-liquidation, une liquidation externe si le taux de garantie approche un seuil critique, ou encore sans fermeture immédiate, en attendant un rebond du prix).
Lorsqu’un utilisateur dépose une garantie et emprunte une stablecoin, le contrat intelligent LLAMMA détermine la bande correspondante. À mesure que le prix de la garantie évolue, elle est convertie en stablecoin. Quand le système est « sous-eau », l’utilisateur dispose déjà de suffisamment de USD pour rembourser son prêt. Le montant de stablecoin disponible peut être calculé via la méthode publique get_x_down. Si cette valeur est trop proche du seuil de liquidation, des liquidateurs externes peuvent intervenir (bien que cela ne devrait pas survenir pendant plusieurs jours, voire semaines, après une chute suivie d’un plateau, ou jamais si le prix ne remonte pas ou remonte rapidement). Lorsque le prix est nettement au-dessus du seuil de « liquidation », un indicateur sain consiste à examiner le ratio entre get_x_down et la dette, auquel on ajoute la valorisation de la garantie.
Lorsque la stablecoin génère des intérêts, cela doit se refléter dans l’AMM. Cela se fait en ajustant toutes les grilles de prix. Ainsi, lorsque la stablecoin perçoit un taux d’intérêt r, toutes les grilles de prix de l’AMM sont décalées vers le haut au même taux r, via un multiplicateur appliqué au prix de base. Tant que le taux perçu est positif, ce multiplicateur augmente progressivement dans le temps.
Lorsque nous calculons get_x_down ou get_y_up, nous déterminons d’abord les quantités x* et y* de stablecoin et de garantie que l’on aurait si le prix actuel atteignait po. Puis nous évaluons combien de stablecoin ou de garantie nous obtiendrions si po évoluait adiabatiquement jusqu’au prix le plus bas de la bande inférieure ou le plus haut de la bande supérieure. Cela fournit une mesure robuste du montant de stablecoin récupérable, indépendante du prix instantané actuel, ce qui est crucial pour résister aux attaques de sandwich.
Il convient de noter que LLAMMA utilise po, défini comme le prix ETH/USD, comme source de prix. Notre stablecoin peut toutefois s’échanger sous-parité (ps < 1) ou au-dessus (ps > 1). Si ps < 1, alors le prix dans LLAMMA est p > po.
Dans l’approximation adiabatique, p = po / ps, et toutes les conversions garantie ↔ stablecoin se produisent à un prix d’oracle effectif plus élevé, équivalent à :
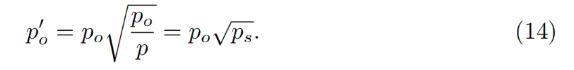
À ce prix, la quantité de stablecoin obtenue lors de la conversion est multipliée par un facteur 1/ps (si ps < 1).
À long terme, une situation où ps > 1 n’est pas souhaitable. C’est pourquoi nous utilisons un stabilisateur (voir section suivante).
Stabilisateur automatique et politique monétaire
Lorsque ps > 1 (par exemple, en raison d'une demande accrue pour la stablecoin), une réserve d’ancrage est créée par des dépôts asymétriques entre la stablecoin et la monnaie de référence (ou des jetons LP) dans un pool stableswap Curve. Dès que ps > 1, le contrat PegKeeper peut frapper des stablecoins non collatéralisés et les déposer unilatéralement dans le pool stableswap, de sorte que le prix final reste ≥ 1. Lorsque ps < 1, PegKeeper peut retirer (de façon asymétrique) et brûler des stablecoins.
Ces actions provoquent une dépréciation rapide lorsque ps > 1 et une appréciation lorsque ps < 1, car les dépôts et retraits asymétriques modifient le prix. Même si cette partie de l’émission est non collatéralisée, la stablecoin semble implicitement soutenue par la liquidité présente dans le pool. Sur l’ensemble du cycle d’émission et de destruction, le mécanisme apparaît profitable tout en assurant la stabilité.
Soit dst la quantité de stablecoins émise au stabilisateur (dette), et fdx() la fonction qui calcule, via get_dx de l’AMM stableswap, la quantité d’USD nécessaire pour acheter les stablecoins. Pour éviter que la « réserve » ne devienne excessive, nous utilisons un mécanisme de stabilisation « lent » en ajustant progressivement le taux d’intérêt r.

où h représente la variation de ps, et la variation du taux r est doublée (plus ps est élevé, plus r est bas). La dette dst du stabilisateur s’équilibrera à différentes valeurs selon ps = 1 et r₀. Ainsi, plutôt que de régler manuellement r₀, on peut le diminuer lorsque dst/supply dépasse un certain seuil cible (par exemple 5 %), incitant les emprunteurs à prendre des crédits et vendre la stablecoin, abaissant son prix et forçant le système à brûler dst ; inversement, on peut l’augmenter lorsque dst/supply est faible, incitant au remboursement des prêts, ce qui pousse ps à remonter, forçant le système à accroître dst et les dépôts du stabilisateur.
Conclusion
Nous espérons que le mécanisme proposé permettra de résoudre les risques associés aux liquidations dans les systèmes de stablecoins et de prêt.
En outre, le stabilisateur et le mécanisme de politique monétaire automatique peuvent aider à maintenir la parité sans nécessiter un module de stabilité de parité (PSM) excessivement volumineux.
Bienvenue dans la communauté officielle TechFlow
Groupe Telegram :https://t.me/TechFlowDaily
Compte Twitter officiel :https://x.com/TechFlowPost
Compte Twitter anglais :https://x.com/BlockFlow_News