BiB Exchange：流動性金融奇蹟，揭秘對沖邏輯，化解無常風險

撰文：BiB Exchange

引言

在加密世界的中，Uniswap/Curve 等平臺無疑是一顆顆璀璨的金融明星。然而，當投資者面對無常風險時，如何聰明地實現對沖，已成為他們所面臨一項重要任務。在這次對沖邏輯的探索之旅中，BiB Exchange 將深入流動性核心，探討期權和永續合約等工具如何成為化解無常風險的得力助手。

LP（Liquidity Providers）是目前 DeFi 板塊常見的業務類型之一，LP 主要用於為交易提供流動資金池，用於在賺取交易中的流動性挖礦中賺取複利、取得加密貨幣貸款，或轉讓質押流動性的所有權。其本質是基於 AMM（Automated Market Maker）算法下的做市業務，LP 通過將兩種或多種代幣存入資金池中，來為交易提供流動性，並從交易手續費中獲得收益，但這種方式往往面臨著無償損失的風險。

本文，BiB Exchange 主要介紹以下三個部分：第一部分介紹市場上常見的 AMM 機制及其特徵；第二部分以 Uni V2 介紹了無常損失及其函數特徵；第三部分介紹了幾種常見的無常損失對沖方法：動態對沖、永續動力、期權，並對比其優劣。

一、從 AMM 談起

用戶通過向流動性資金池提供流動資金，即成為流動性提供者 ( Liquidity Providers)。流動性池的背後原理即採用了自動做市商（Automated Market Maker，AMM）機制，更具體的說，它叫做恆定函數做市商（Constant Function Market Makers，or CFMMs) 機制。其在去中心化平臺上實現，不需要傳統中介，可支持多資產交易對，並且還具備以下幾個明顯特徵：

1. 無需訂單簿：與傳統的中心化交易所不同，AMM 不依賴於傳統的買方和賣方訂單簿。交易是直接在智能合約中執行的，而不是通過撮合買賣訂單。

2. 交易費用：每筆交易都會向流動性提供者收取費用，這些費用是根據其提供的資金在交易中的份額來計算的。這種模式鼓勵用戶提供更多流動性，從而促使市場更加活躍。

3. 價格連續調整：由於 AMM 使用的算法，資產價格會根據供需關係持續調整。這使得在交易中即時獲得對應數量的資產成為可能，而不需要等待訂單被撮合。

目前市場頭部 Dex 平臺常見的 AMM 算法有以下幾種：

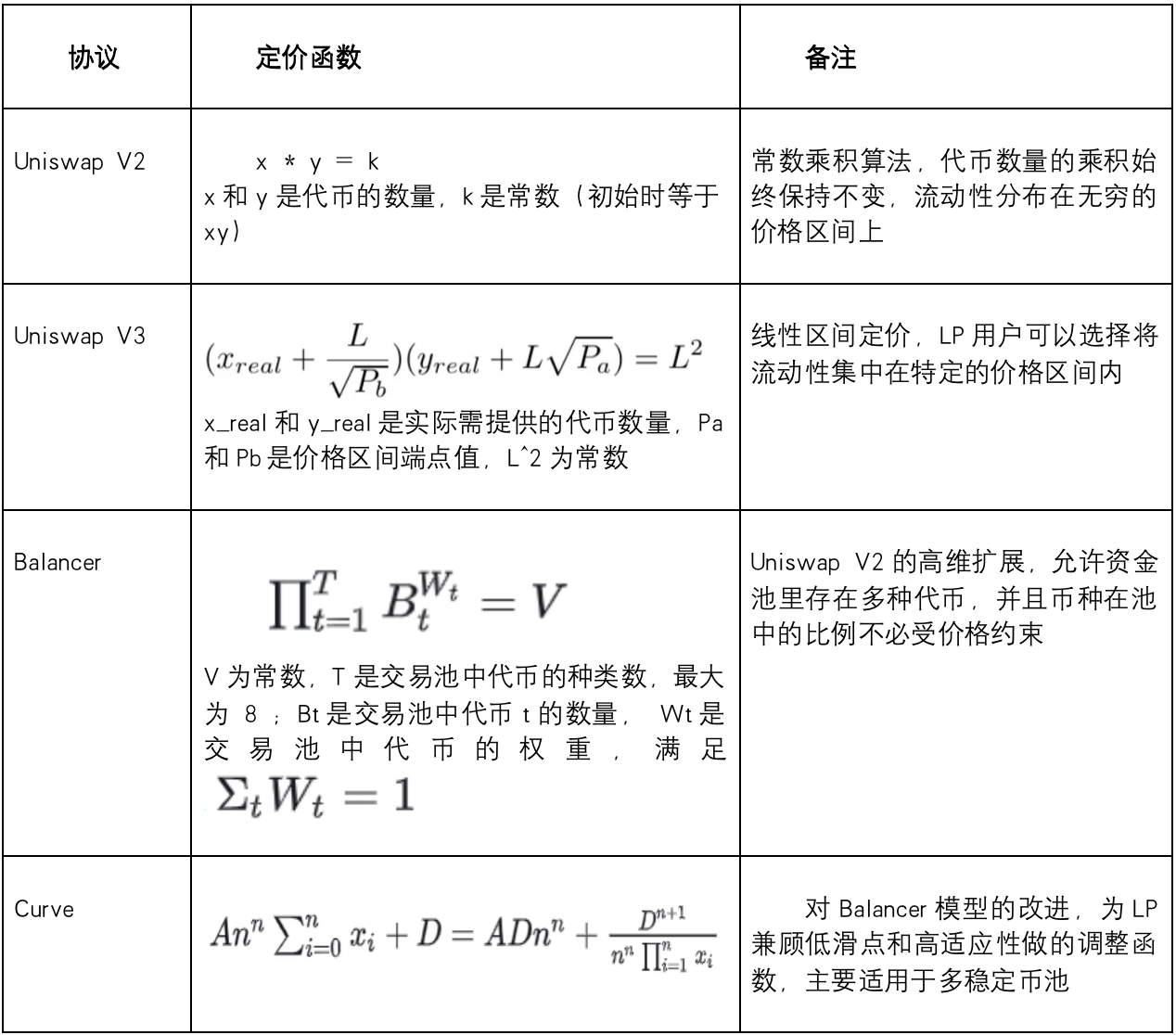
在這些協議中，交易者在進行交易時支付一定比例的手續費，其中的一部分作為獎勵分配給流動性提供者。然而，由於無常損失的存在，流動性提供者需要權衡提供流動性所獲得的手續費和可能的損失。

但同時，在流動性提供者存入資產到資金池期間，數字資產的價格如果發生任何波動，市場價格的波動與流動性池的價差將產生套利空間。套利者會不斷地進行套利操作，直至資產比例變動接近市場真實的價格。在這期間，流動性提供者從套利者的交易中獲取了費用；而套利者從中獲取價差利潤，即導致流動性提供者產生潛在損失 -- 無常損失。

二、函數特徵

以 Uniswap V2 的 AMM 機制為例，BiB Exchange 將帶大家來看一下無常損失是如何發生的。它通過 X*Y=K 來計算流動池內的兩種貨幣價格。其中 X 與 Y 分別為兩種資產存量，K 為常數。

假設流動性池裡的兩種資產 X 和 Y 分別為 ETH 和 DAI，用戶在流動資金池中存入 1 ETH 和 100 DAI。在對應自動做市商（AMM）機制中，要求存入數字貨幣的資金對必須具有同等價值。這意味著在存款時，1ETH 價格=100 DAI。那麼，用戶存款資產價值為 200 美元。如此時資金池中總共有 10 ETH 和 1,000 DAI，總流動資金為 2000 美元。那麼，用戶在資金池中佔有 10％的份額，常數 K=10*1000=10,000。

此時，我們假設 BiB Exchange 的現貨 ETH 市場價格上漲到 400 DAI，而資金池中 ETH 價格仍為 100 DAI。此時套利交易者發現套利機會，會將 DAI 添加到池中並從池中移除 ETH，直到資產比例變動至接近市場價格。根據恆定乘積原理，常數 K 為 10,000。如忽略交易費，流動池內共有 5 ETH 和 2,000 DAI。

如果用戶決定此時提取資金，根據其資金池中所佔的 10% 份額，他可以提取 0.5 ETH 和 200 DAI，總計 400 美元。雖然此時用戶是盈利的，但如果該用戶選擇不成為流動性提供者，而只是持有 1 ETH 和 100 DAI，他可獲得 500 美元！由此可見用戶成為流動性提供者，與僅持幣相比，損失了 100 美元。這 100 美元即為用戶的無常損失。

注：該案例忽略了用戶成為流動性提供者可獲取的手續費。

下面進行簡單的推導：

我們定義 ETH 對穩定幣 DAI 的價格為 P，則 P=Y/X

聯立 X*Y=K ，P=Y/X 這兩個方程可以得到：

X = (K/P)^0.5；Y = (K*P)^0.5

對於兩個時刻 T0 和 T1，價格分別為 P0 和 P1，其中 P1=*P0，為價格變化倍數

則 T1 時刻流動性池的價值為 2*Y1 = 2* (K**P0)^0.5；

不進行 LP，T1 時刻原有資產的價值為 X0*P1+Y0 = (1+)*(K*P0)^0.5

無常損失 = [ X1*Y1 - (X0*P1+Y0) ] / (X0*P1+Y0) = 2^0.5/(1+) - 1

= -(^0.5 - 1)^2 / (1+) <= 0 恆成立；

可以看出，只要價格有變動，那麼 LP 必然遭受無常損失。

下圖為不同價格變化幅度下無常損失的函數圖：

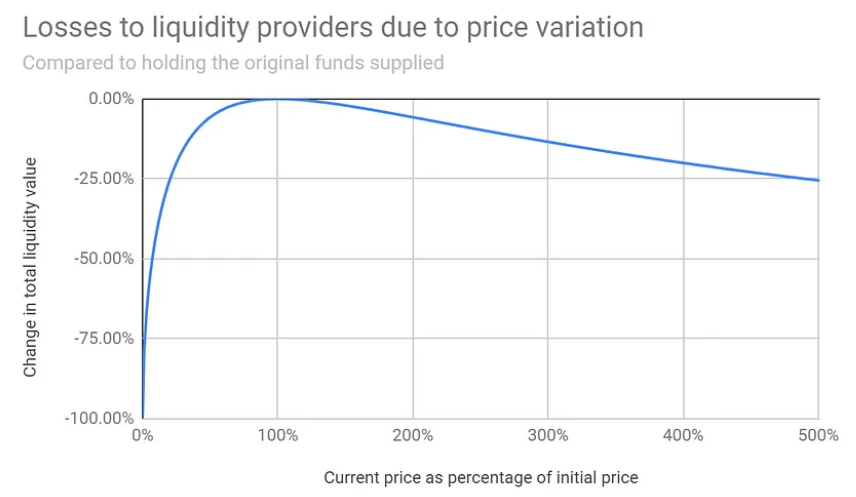
通過圖表可以看到，與單純持幣相比，幣價波動越大，無常損失越大。但如該無常損失小於所賺取的手續費，用戶仍可盈利。

對於其餘常見的 AMM 機制，其無常損失函數均類似，即價格波動會造成 LP 遭受無常損失，那麼如何避免無常損失呢？下面我們看看有哪些思路來處理無常損失。

三、無常損失對沖

假設流動性池裡的兩種資產 X 和 Y 分別為 ETH 和 DAI，用戶在流動資金池中存入 1 ETH 和 100 DAI。此時兩者的價值相等，即 ETH 的價格 P = 100 / 1 =100。

以上面的組合（50% 持有波動資產，50% 持有穩定幣）作為基準（基準組合不唯一，也可以全部持有波動資產作為基準），帶大家一起來看看如何規避無常損失。

對於 50% : 50% 的投資組合的價值是 V_HODL_50() = (1+)*(K*P0)^0.5，這是關於（價格變動）的一個線性函數。

而 LP 的價值函數 V_LP() = 2* (K**P0)^0.5 是關於的一個平方根函數，是非線性的，這種非線性存在於所有合理的 AMM 機制（具體函數形式有差別）。

這裡我們再引入兩個概念：

• delta：投資組合價值函數相對於價格的一階導數，它代表投資組合價值相對於價格的變化率。

• gamma：投資組合價值函數相對於價格的二階導數，是 delta 相對於價格的變化率。

可以發現，基準價值函數的 gama 值始終為 0，而 LP 價值函數的 gamma 值始終為負。

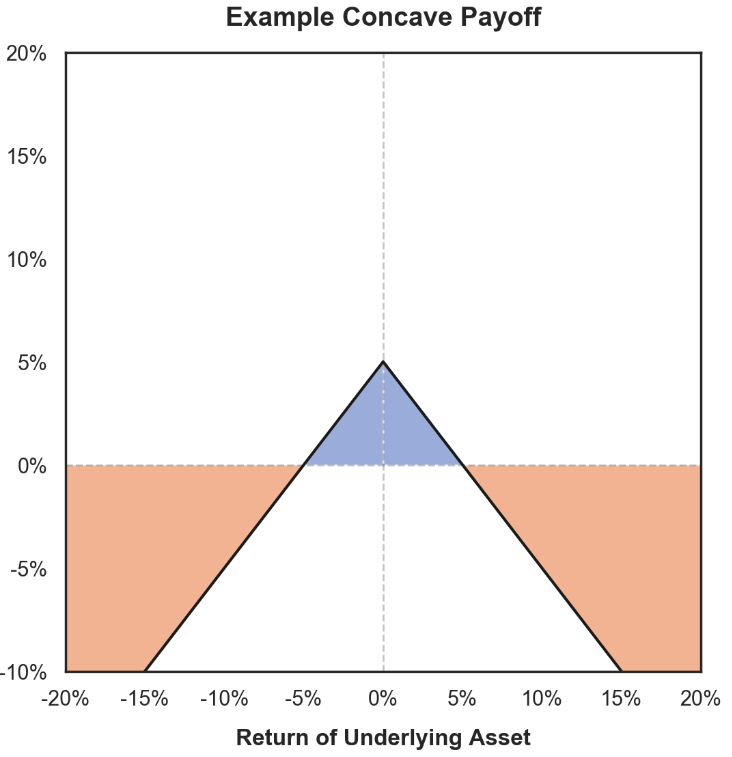
負伽馬收益：價格上漲時利潤減少，下跌時損失放大

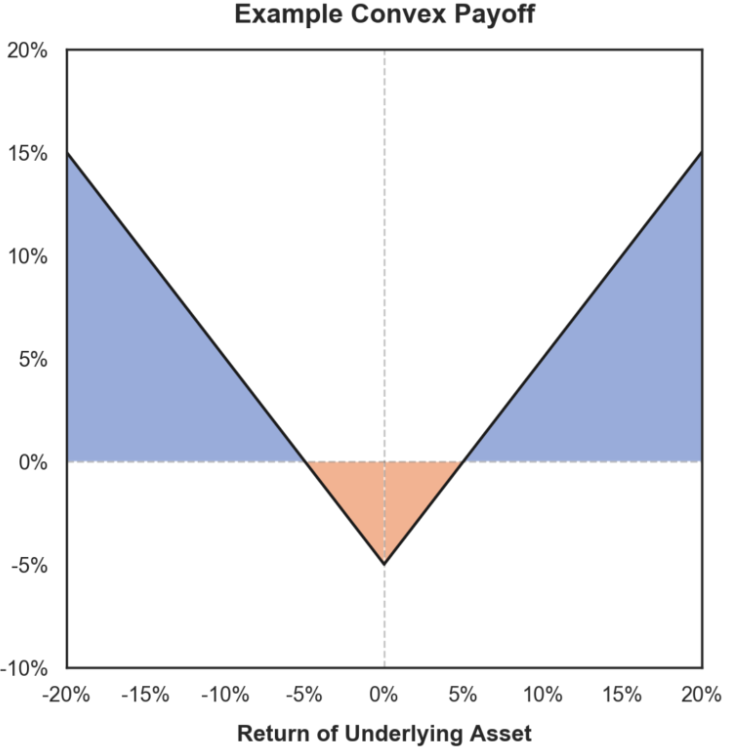
正伽馬收益

那麼我們怎麼應對這種負伽馬的情形呢？BiB Exchange 團隊認為有以下幾種方法：

1）最大化費用收入。當費用收入大於無常損失時，LP 是有利可圖的；

2）尋找波動性較小的貨幣對；

3）當價格發生變化時，動態地重新對沖頭寸；

4）通過購買具有正伽馬的金融工具（例如期權和永續動力合約）來對沖頭寸。

3.1 永續合約

最大化費用收入：從本質上講，它通常是選擇一個好的池子，選擇一個好的費用等級，猜測市場下一步會做什麼：更類似於交易而不是被動投資。不僅要考慮礦池的 APY，還可以使用隱含波動率指標（(Implied Volatility, IV) 是根據期權的市場價格反推計算出來的未來股價波動率。）或計算礦池的夏普比率（(Sharpe Ratio) 是用來衡量投資組合每承受一單位總風險所獲得的超額報酬,它等於投資組合的超額報酬率與投資組合的標準差之比。）。

尋找波動性較小的貨幣對：穩定貨幣對通常不會遭受無常損失，但是，存在小概率脫鉤風險，可能導致災難性損失。

動態對沖：讓我們看看通過借貸對沖的 DeFi 原生策略。與通過永續合約進行對沖相比，它需要更多的前期資金，但相對安全且易於執行。

Alice 從 5000 USDC 開始，並在 USDC/ETH 池中提供流動性。ETH 的初始價格為 1000 USDC。

Alice 將 4000 USDC 放入 Aave，借入 1 ETH，以 50：50 的比例將資產置於全範圍 Uniswap 頭寸中。

初始資本為 5000 USDC，分為對沖（價值 3000 USDC）和池（價值 2000 USDC）：

V_collateral = 4000

V_debt = 1000 V_hedge = 4000–1000 = 3000

V_capital = V_pool +

V_hedge = 5000

ETH 價格上漲兩倍，達到 2000 USDC。現在池中的值是 2000 ·sqrt（2）USDC，但對沖的價值下降到 2000 USDC：

V_collateral = 4000 V_debt = 2000 V_hedge = 4000–2000 = 2000

V_capital = V_pool +

V_hedge = 2000

（1 + sqrt（2）） = 4828 USDC

相對於初始資本有 3.4% 的損失。除了機會成本外，沒有對沖成本，因為借貸費用不太可能超過貸款的年利率。

Bob 以相同的初始資本和相同的策略開始。然而，當 ETH 價格達到 1500 美元時，Bob 注意到流動性現在包含不到 1 個 ETH，因此可以在保持頭寸完全對沖的情況下償還部分借入的 ETH。Bob 從 Aave 中取出一些 USDC，將它們換成 ETH，償還 ETH，因此借入的 ETH 數量正好等於流動性頭寸中的 ETH 數量。當 ETH 價格達到 2000 美元時，Bob 的投資組合仍有一些損失，但他的損失低於 Alice。

直觀的解釋是這樣的：如果 Alice 現在想償還貸款，她必須以 2000 美元的價格購買 ETH，而 Bob 以 1500 美元的價格購買一些 ETH。

但是，如果價格再次從每 ETH 1500 美元變為 1000 美元，則 Bob 產生了交易成本和掉期成本，而 Alice 則沒有。此外，在這次價格下跌之後，Bob 不得不向相反的方向重新平衡：他借入更多 ETH，將其出售為 USDC，並將 USDC 作為抵押品放入 Aave。

下面我們用數學形式來表達，前面我們知道無常損失的公式：

DL() = -(^0.5 - 1)^2 / (1+) <= 0

且 V_HODL_50() = (1+)*(K*P0)^0.5；V_LP() = 2* (K**P0)^0.5

我們可以使用 HODL 倉位的值和無常損失項來分解 LP 倉位的值：

V_LP() = V_HODL_50() + V_HODL_50() * DL()

假設目標是 delta 中性對沖。應該構建對沖投資組合，使其與 HODL 50:50 投資組合具有反向收益：

V_hedge（_H） ：= V0 - V_HODL_50（_H）

這裡_H 表示構建對沖投資組合的價格比率。如果 = _H，那麼這是一個真正的 delta 中性組合投資組合，這意味著波動性資產價格的微小變化不會對投資組合的價值產生重大直接影響。

V_portfolio（） =

= V_HODL_50（） + V_HODL_50（）*DL（） + V_hedge（） - hedging_costs

= V0 + V_HODL_50（）*DL（） — hedging_costs

注：

a.非線性函數：V_HODL_50（）*DL（）項（恆小於等於 0）表示由於價格變化而造成的損失。當 =1.0 時，它等於零。通過保持較小的價格變化，該項可以保持在接近零，因為它是價格變化的非線性函數。

b.Hedging_costs 描述了購買或出售對沖資產的成本，主要包括交易費用和價格影響。

這個想法是每當 增長或減少超過某個固定閾值時重新平衡對沖。我們稱這個閾值為再平衡步驟。

為了將每步的資本損失保持在有限範圍內，每當價格變化超過再平衡步驟時，LP 都會重新平衡他們的對沖。套期保值成本隨著步長變小而變大，但無常損失項 V_HODL_50（）*DL（）可以根據需要做到儘可能小。火幣的單幣無損挖礦即是採用這種機制。

c.選擇動態再對沖頻率：V_portfolio（）價值方程足以計算我們想要的指標：對沖再平衡步長如何影響價格變化下投資組合的價值變化。

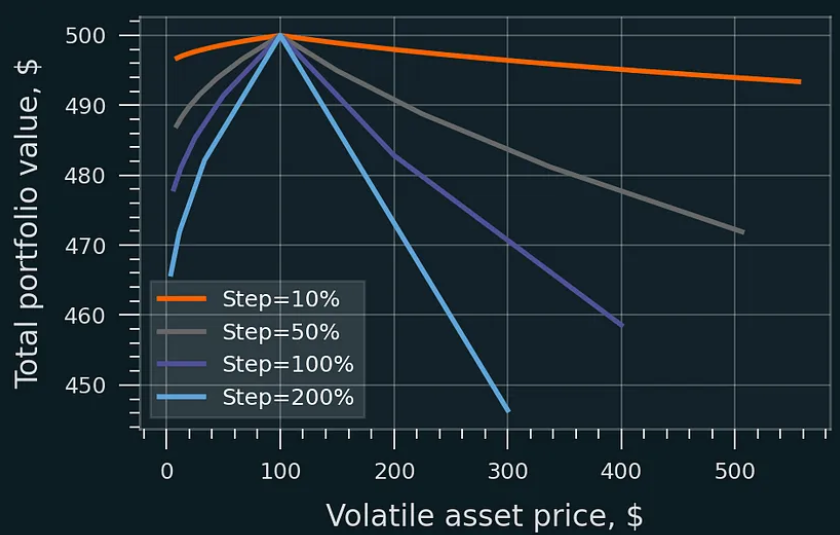
較小的再平衡步驟可降低損失。再平衡成本和賺取的 LP 費用未計入該數字。初始資產價格為 100 美元，LP 頭寸的初始價值為 200 美元。

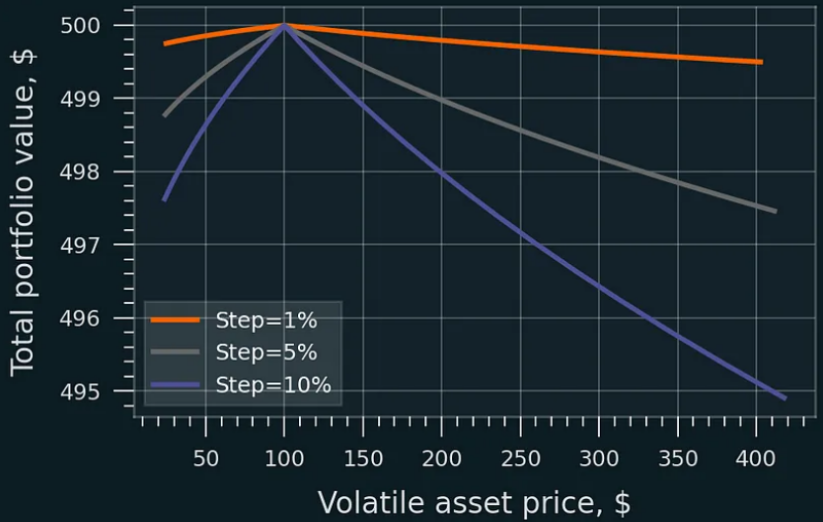
通過非常小的再平衡步驟，無常損失就會消失。再平衡成本和賺取的 LP 費用未計入該數字。初始資產價格為 100 美元，LP 頭寸的初始價值為 200 美元。

下圖顯示了通過 GBM（隨機遊走模型）模擬估算的對沖成本，假設 0.3% 的掉期費，沒有交易費。在 Uniswap V2 版本的全範圍頭寸中，即使是小規模的對沖再平衡步驟（1% 至 2%）也成本較低：

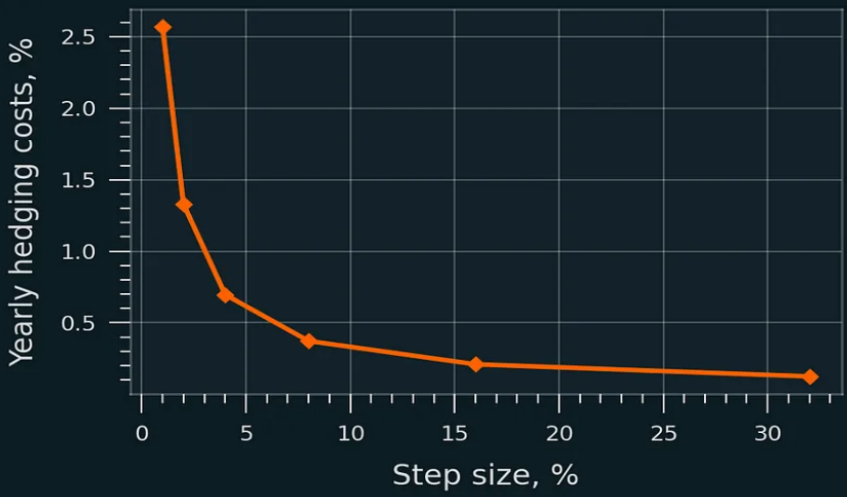
再對沖的年度掉期成本佔初始資本的百分比；Uniswap v2。在流動性集中的情況下，對沖成本較高，但相對於初始資本仍然很小：

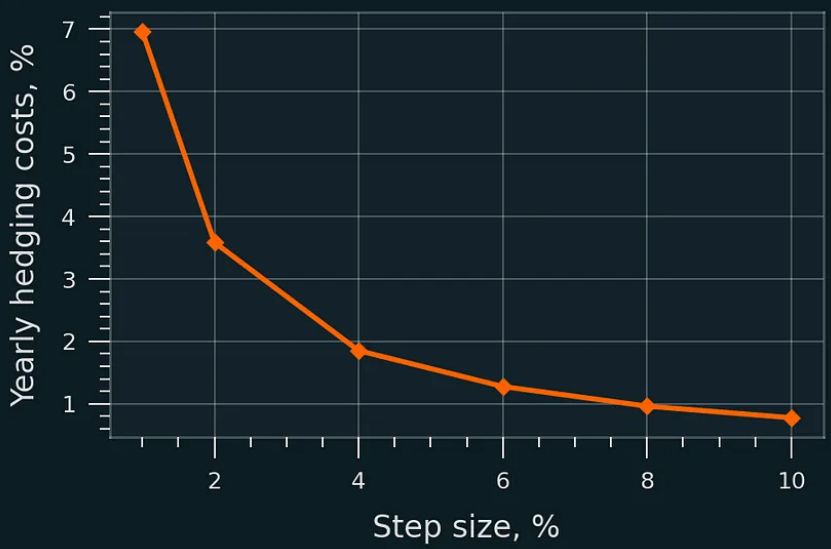
再套期保值的年度掉期成本佔初始資本的百分比；Uniswap v3；價格範圍：[P/1.5，P*1.5]，無流動性遷移。

到目前為止，討論主要集中在全範圍的 delta 中性策略。但是，相同的策略可以應用於其他情形。例如，只有 50% 的波動性資產允許借入。這將給出一個混合策略，其中 1/2 的初始值遵循 sqrt（） 函數，另外 1/2 是 delta 中性的。

此外，借款金額本身可能是價格的函數。假設在初始價格下，LP 借入了所需波動性資產的 100%，但隨著價格上漲，他們慢慢將借入的資產減少到零。如果價格低於初始價格，則反其道而行之：借入和交換穩定幣超過所需資產的 100%。它在下圖中顯示為凸函數：

與 HODL 策略相比，部分和動態對沖。步長=1%。不顯示賺取的費用。

另外需要注意的是：對於具有固定價格範圍的 Uniswap v3 頭寸，重新平衡對沖應與資金池中的流動性重新定位相結合。

關鍵要點：

a.通過對沖和定期重新平衡對沖，LP 可以保護其資本免受價格下跌和價格上漲的影響，Delta-neutral 策略是可實現的。

b.如果 LP 使用「x% 的價格變化」作為對沖再平衡過程的觸發因素，則可以將背離損失降至最低。

c.用於觸發套期保值更新的價格步長越小，剩餘無常損失越小。但是，使用較小的再平衡步長會導致更高的對沖成本。

3.2 永續動力

購買具有正伽馬的金融工具：下面 BiB Exchange 團隊將為大家介紹兩種工具，永續動力（Power Perpetuals）和期權，我們先討論永續動力合約。

永續動力合約：這是一個較新的概念，即某些資產價格的冪函數（平方、立方或更高階）。如果 ETH 的價格翻倍，則 ETH^2 永續動力價格是原來的 4 倍，ETH^3 永續動力價格是原來的 8 倍，ETH^5 永續動力價格是原來的 32 倍。

下圖是永續動力和對應槓桿倍數的永續合約回報率比較：

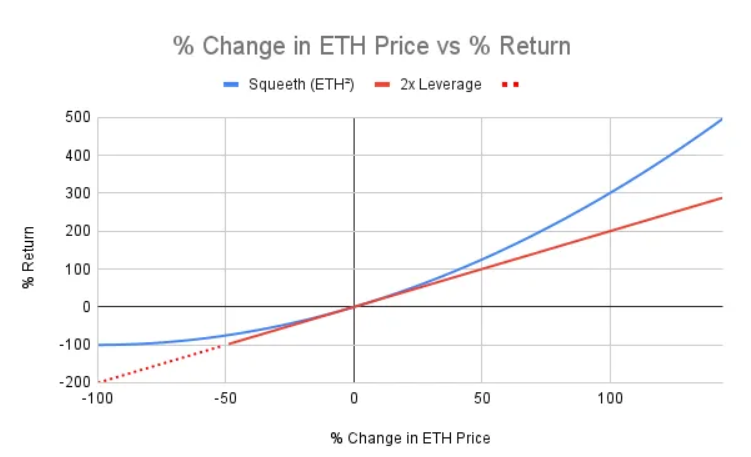
ETH² 永續 （Squeeth） 在價格上漲時提供比 2 倍槓桿更高的回報，在價格下跌時提供更低的損失。

下面我們來看一個案例：

Alice 擁有她想要對沖的全分佈 USDC/WETH 流動性頭寸 P。她查閱了相關的參數表：

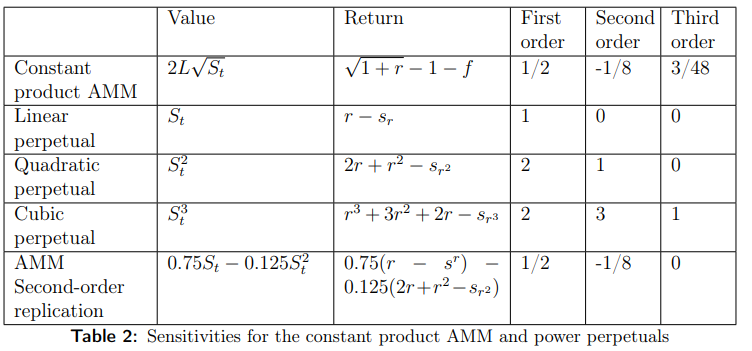
我們先來解釋上面的表格含義：

• Value 代表了不同模型下的組合價值函數；

• Return 代表了回報率，其中 r 代表接近於零的價格變化，「Sr、Sr²、Sr³」表示一階、二階和三階永續合約的資金費率，注意，這裡對回報率的計算採用了泰勒展開的方法；

• First，Second，Third order 代表了回報率函數泰勒展開的各階係數。

Alice 發現她需要獲得 50% 的 ETH 空頭敞口和 12.5% 的平方 ETH 多頭敞口（該百分比是根據 V（LP） 計算得出的，V（LP） 是鎖定在 LP 頭寸中的資本總價值）。她像往常一樣做空 ETH（使用簡單的永續合約，或者使用借來的 ETH 到 LP），然後前往 Opyn 或其他 power perp 協議，購買所需數量的 Squeeth。Squeeth（「平方 ETH」）是 ETH 的衍生資產，它隨著 ETH 價格的平方而改變其價格。

如果有更高階的永續動力合約可用，她也可能得到 3/48 * ETH³ 的 V（LP） 長和 15/384 * V（LP） 短於 ETH⁴，依此類推。

如果 Alice 想匹配 50 : 50 的 HODL 投資組合，她不會做空 ETH，而是直接買入 2 階和更高階的永續動力（見下圖）。

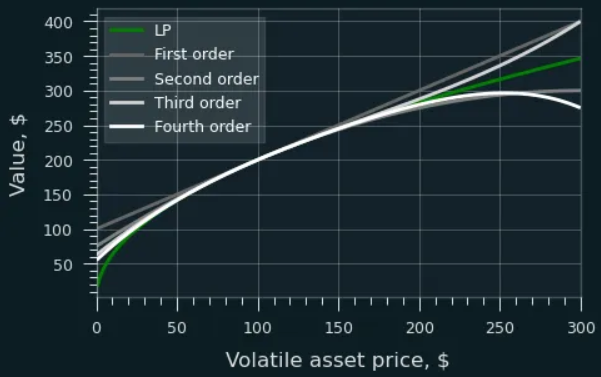
LP 的值函數可以由一系列永續動力來近似。高階永續動力更準確地接近 LP 值。

上圖顯示了 LP 的收益函數如何通過一系列冪永續合約擬合。永續合約仍然需要偶爾重新平衡，但與簡單的線性對沖需要在每 1% 或 5% 的價格變動時進行重新平衡不同，即使在 50% 或 100% 的價格變動範圍中這樣做，也可以提供足夠的對沖準確性。

但是目前市場上很少有協議提供永續動力，只有 Opyn 的 Squeeth 已經確立了自己的地位，甚至 Squeeth 在市場上也沒有大量的流動性。BiB Exchange 團隊認為，這種模擬方法的實用性不足。

3.3 期權

1. 確定您的策略位置：

假設初始 ETH 價格為 1000 美元。讓我們從 1000USDC 開始（作為基準線）。我們以 ETH 出售其中的 50%：

x0 = 0.5 ETH

y0 = 500 USDC

我們在 ETH-USDC 池中 LP 0.5 ETH 和 500 USDC。

2. 計算策略頭寸的收益曲線。

Uni V2 LP 值：V = 2*L*S^0.5 + 費用

S = ETH 的現貨價格

L = （x0 * y0）^ 0.5

減去我們的初始資本：

收益 = 2*L*S^0.5 + 費用 - 1000

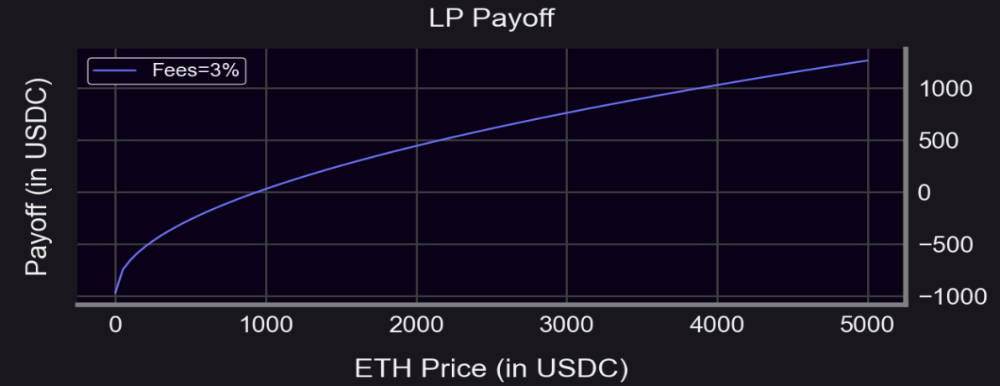
對於 Uni V3 而言，則更復雜些：

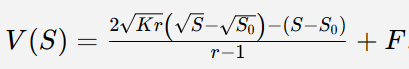
其中：

F = 累計費用；

K = ( 價格上界 ⋅ 價格下界 ) ^ 0.5；

S0 = 起始價格；

r = ( 價格上界 / 價格下界 ) ^ 0.5。

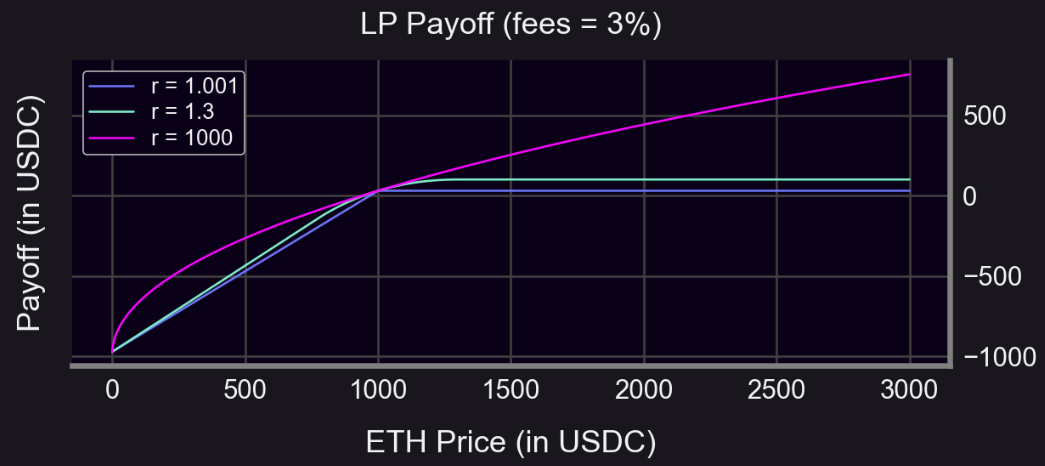
可以發現，r 越大，LP 收益曲線越接近 Uni V2。並且可以看到，在區間的外側，收益結構和期權類似，所以我們可以採取以下方法：

初始 ETH 價格 = 1000

買入 1 ETH 的平值看跌期權（行權價 = 1000 美元）

看跌期權費 = 50

LP 費用 = 3% （r = 1.3，區間為 初始價格 /1.3 至 初始價格 *1.3)

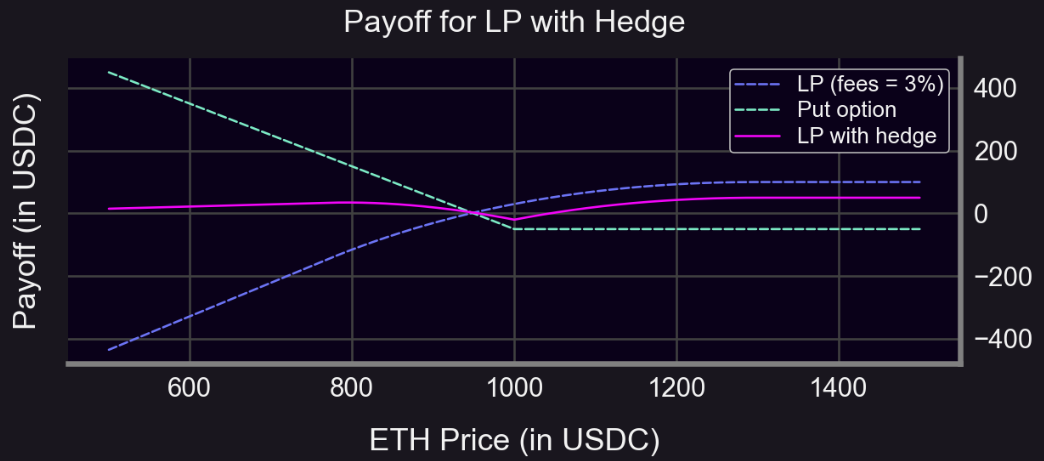
S < 1000 時：對沖收益更平坦（有時是正的）

S ≥ 1000 時：對沖收益較低（由於溢價）

套期保值總是要花費美元。我們需要賺取足夠的費用來支付對沖價格。

如果我們以 50 : 50 ETH-USDC 的組合作為基準，我們可以通過跨式期權來對沖：

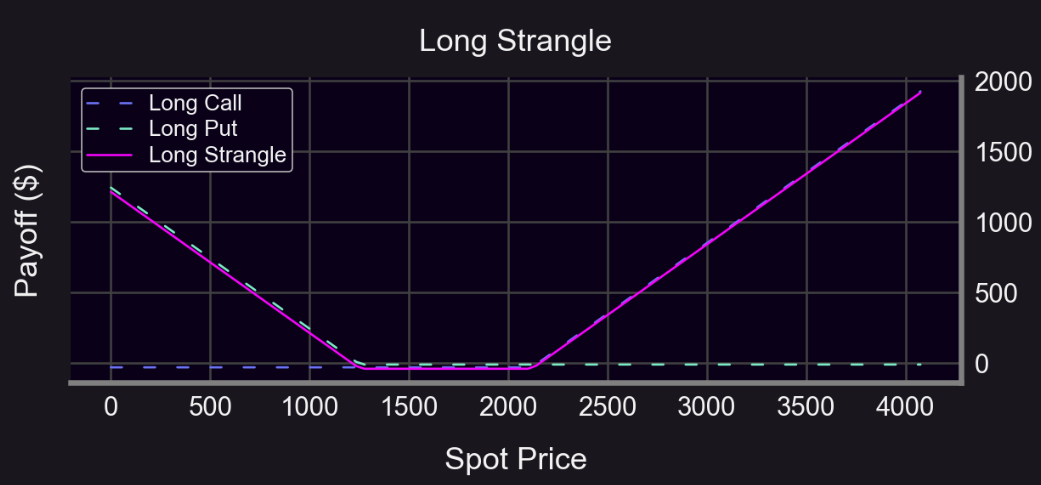
不難發現，通過跨式期權，即使在看漲和看跌期權都比較大的劇烈行情下，可以得到一個相對小金額的無常損失如下圖：

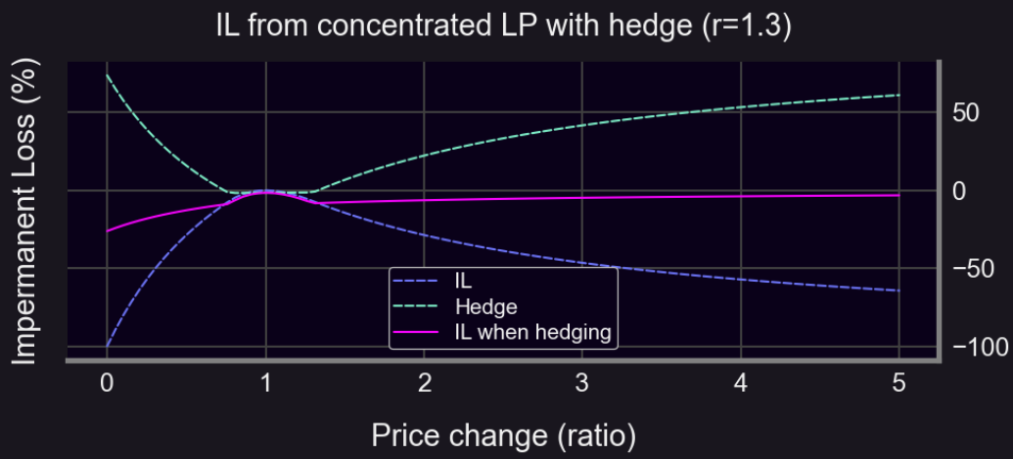
Panoptic 提供永續期權用以對沖。持有永續期權的用戶可以選擇進行對沖操作，以降低其風險。同時，流動性提供者可以參與提供對沖所需的流動性，並從手續費中獲得回報。Panoptic 提供的永續期權也為 Uniswap 的對沖提供了另一種可能。BiB Exchange 團隊認為，通過對沖 gamma，我們得以更全面地管理風險，同時又能享受永續動力的流動性。

我們總結下用不同工具對沖的優缺點，注意，這只是一般性的對比，實際效果可能受到具體情況和市場狀況的影響。

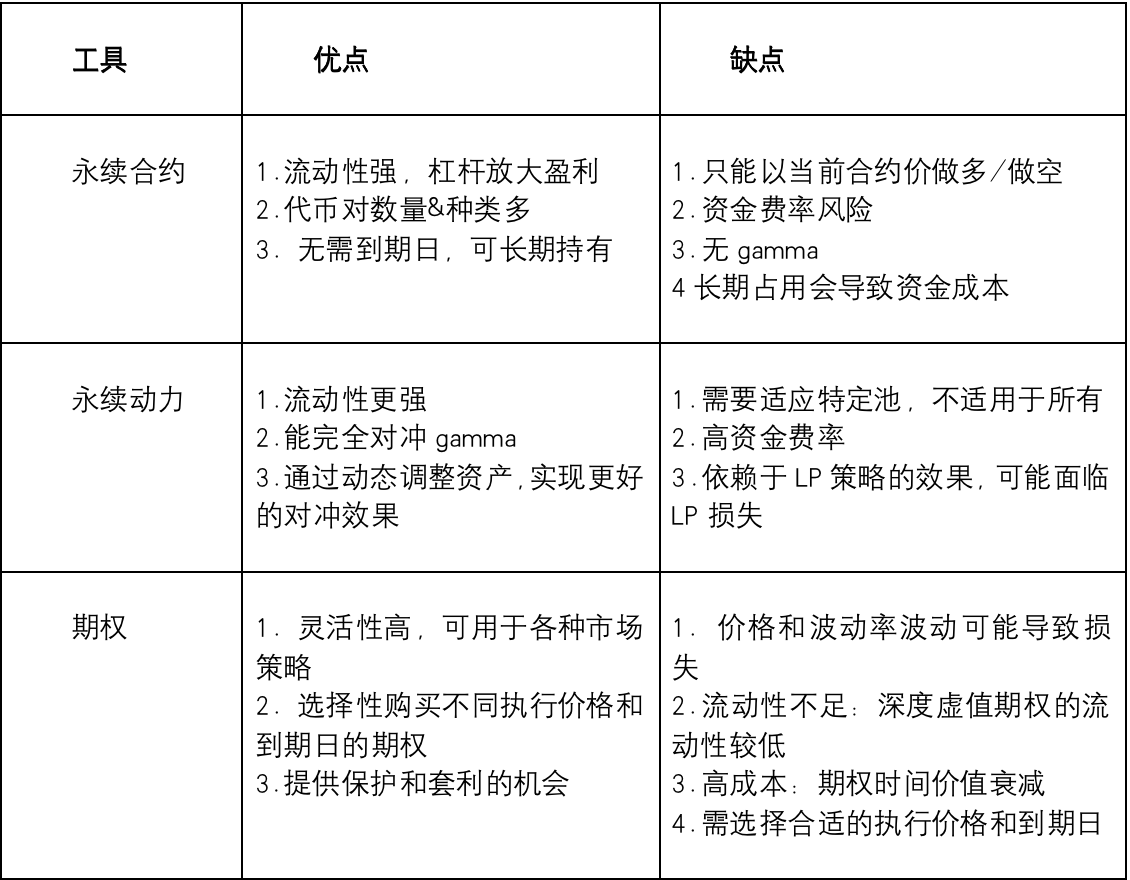
小結：

通過以上分析不難發現，為了規避無常損失，各類對沖工具都會有一定的交易成本，我們需要權衡 LP 收取的交易費用和對沖成本之間的關係，想要取得比較理想的無風險回報並非易事。每種對沖工具都有其利弊。永續合約和永續動力雖然流動性強，但也伴隨著資金費率風險。而期權則因為流動性不足和高成本而受限。

BiB Exchange 團隊認為，在這個市場所演變的流動性金融奇蹟中，對沖邏輯是我們航行的明燈，也是我們攀登金融高峰的得力工具。而身處其中，投資者們需要權衡 LP 收費和對沖成本，謹慎思考，在各類對沖工具中謹慎取捨，以找到最適合自己需求的對沖方案。