
스탠퍼드 블록체인 클럽: 제로지식 증명에도 무어의 법칙이 존재, 초당 생성되는 증명은 매년 두 배씩 증가
작성: STANFORD BLOCKCHAIN CLUB, ROY LU
번역: TechFlow
참고: 본문은 스탠퍼드 블록체인 리뷰에서 제공한 내용이며, TechFlow는 스탠퍼드 블록체인 리뷰의 파트너로서 독점적으로 번역 및 전재할 권한을 부여받았습니다.

서론
본 글에서는 제로노울리지 프루프(ZKP) 기술이 Web3를 넘어 우리의 삶을 어떻게 변화시킬 수 있는지 살펴볼 것입니다. 저는 성능 향상의 핵심 요소들을 논의하고 “제로노울리지의 무어의 법칙”이라는 개념을 제안하며, 가치 축적 패턴을 분석하겠습니다.
제로노울리지(ZK)는 현재 Web3 분야에서 가장 혁신적인 기술 중 하나로, 확장성, 신원 인증, 개인정보 보호 등 다양한 분야에서 큰 가능성을 지니고 있습니다. 그러나 현재의 성능 수준은 많은 잠재적 활용 사례의 실현을 제한하고 있습니다. 하지만 ZK 기술이 계속 성숙함에 따라, 저는 이 기술이 지수급으로 성장하여 Web3뿐 아니라 전통 산업 전반에 걸쳐 광범위하게 적용될 것이라 믿습니다. 무어의 법칙이 반도체 칩 내 트랜지스터 밀도가 2년마다 두 배로 증가한다고 예측했듯이, 저는 제로노울리지 프루프에도 유사한 지수적 법칙이 존재한다고 주장합니다. 구체적으로 다음과 같습니다:
앞으로 몇 년 안에 초당 생성되는 증명 수가 두 배 이상 증가하다가, 점차적으로 기본적인 범용 컴퓨팅 성능 향상 속도와 수렴할 것이다.
무어의 법칙 개요
무어의 법칙은 인텔 공동 설립자 고든 무어(Gordon Moore)가 1965년에 한 예측으로, "반도체 집적회로의 복잡도는 2년마다 두 배씩 증가할 것"이라는 내용입니다. 지난 58년간 이 법칙은 모바일 컴퓨팅과 머신러닝, 디지털 생활 전반에 걸쳐 혁신을 주도하며 인간과 기술 간 상호작용 방식을 근본적으로 변화시켰습니다.
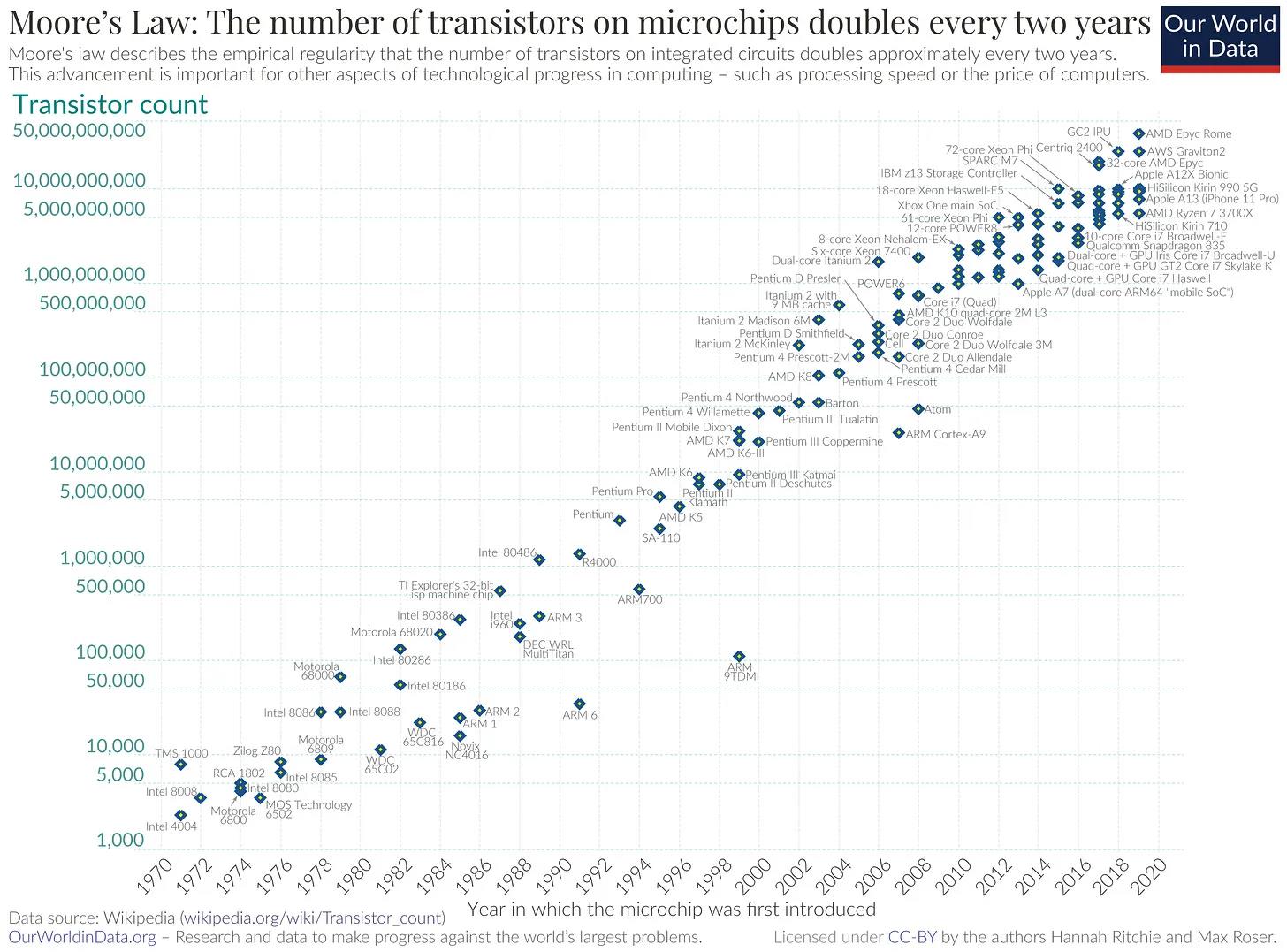
고든 무어는 칩 위 트랜지스터 수가 두 배로 늘어날 때 제조 비용은 규모의 경제 효과로 거의 유지된다는 경험적 관찰을 했습니다. 또한 계산 능력에 대한 수요 증가가 트랜지스터 밀도 향상을 위한 투자를 촉진할 것이라고 지적했습니다.
계산 능력이 점점 더 작아지는 칩 위에서 지수적으로 향상되면서, 트랜지스터 수의 양적 변화는 컴퓨터 사용과 상호작용하는 방식의 질적 변화로 이어졌습니다.
우리의 스마트폰은 아폴로 11호보다 강력한 컴퓨터이며, 주머니에 넣고 다니며 원하는 웹사이트에서 콘텐츠를 스트리밍하거나 세계 어느 곳이든 사람들과 소통할 수 있게 해줍니다. 대규모 언어 모델(LLM)의 훈련은 ChatGPT 출시를 가능하게 하였고, 정보 검색부터 지능적 통합까지 정보와의 상호작용 방식을 완전히 바꾸었습니다.
제로노울리지 프루프와 Web3의 폭발적 발전
트랜지스터 수의 두 배 증가와 무어의 법칙이 현대 기술과의 상호작용 방식을 질적으로 변화시킨 것처럼, 제로노울리지 프루프의 지수적 성장은 새로운 애플리케이션 레이어 경험의 물결을 열어낼 것입니다. 본질적으로 ZKP는 개인 연산, 검증 가능한 정확성, 재귀적 간결성이라는 특성을 통해 개인정보 보호, 정확성, 확장성을 제공합니다. 이러한 특성들은 새로운 컴퓨팅 패러다임으로의 근본적 전환을 의미합니다.
개인 연산(Private Computation)
제로노울리지는 민감한 데이터를 외부에 노출하지 않고도 연산을 수행하고 결과만 공유하며 검증할 수 있게 합니다. 현실 세계의 예로 은행이 ZK 기반 연산을 도입하면 신원 도용을 방지할 수 있습니다. 예를 들어, 사용자는 자신의 신분 정보와 신용 이력을 활용해 대출 승인 프로그램을 실행하면서도 은행에 민감한 데이터를 제공하지 않아도 됩니다. 개인정보는 보호됩니다. Web3에서는 Aleo나 Mina 같은 완전한 프라이빗 L1 네트워크, 혹은 Zcash, zk.money, Elusiv, Nocturne 등의 프라이빗 결제 네트워크가 ZKP 기술로 구동됩니다. 또한 Renegade 같은 팀은 ZKP를 이용해 가격 시장을 교란시키지 않으면서 거래 주문을 공개하는 다크풀(dark pool)을 운영할 수 있습니다. 사용자의 개인 정보를 드러내지 않고도 가치가 전달됩니다.
검증 가능한 정확성 (Provable Correctness)
불투명한 연산 환경에서도 ZKP는 입력값, 출력값, 처리 과정에 대해 추적 가능성을 제공합니다. 예를 들어, 분산형 머신러닝은 원격 컴퓨팅 노드 네트워크를 통해 AI 접근의 민주화를 실현할 수 있습니다. ZKP는 머신러닝에서 사용된 데이터, 가중치, 훈련 횟수 등을 증명함으로써 전체 훈련 과정이 의도대로 진행되었음을 입증할 수 있습니다. 즉, 정확성이 보장됩니다. Web3에서는 Gensyn, Modulus Labs 같은 팀들이 zkML을 도입하기 시작했으며, Risc Zero와 같은 일반적인 ZKVM도 개발되고 있습니다. 또한 Polymer, Succinct Labs, Herodotus, Lagrange 등의 ZK 브릿지에서는 체인 간 상태의 정확성을 증명하기 위해 ZKP를 활용합니다. Proven과 같은 애플리케이션은 ZKP를 통해 준비금의 정확성을 입증할 수도 있습니다.
재귀적 간결성 (Recursive Succinctness)
ZKP는 여러 개의 증명을 하나의 증명으로 압축할 수 있습니다. 현실 세계의 또 다른 예로 공급망에서의 진품 추적을 들 수 있습니다. 공급망 각 단계의 제조업체는 민감한 생산 정보를 공개하지 않고도 제품의 진위를 ZKP로 입증할 수 있습니다. 그런 다음 이러한 ZKP를 재귀적으로 결합하여 최종적으로 전체 공급망의 유효성을 입증하는 단일 ZKP를 생성할 수 있습니다. 이는 확장성을 실현합니다. Web3에서는 수천 건의 거래에 대한 ZKP를 하나의 증명으로 통합하여 Starkware, Scroll, zkSync 등의 L2 네트워크를 구동함으로써 블록체인 처리량을 크게 향상시킵니다.
제로노울리지의 무어의 법칙 정의하기
지금까지 살펴본 바와 같이, 트랜지스터의 발전이 애플리케이션 레이어의 폭발을 가능하게 했던 것과 유사하게, ZKP 역시 Web3 혁신을 견인하는 파도를 일으키고 있습니다. 이제 범용 컴퓨팅과 제로노울리지 컴퓨팅을 비교함으로써 ‘제로노울리지의 무어의 법칙’을 구체적으로 정의할 차례입니다.
범용 컴퓨팅과 제로노울리지 컴퓨팅
범용 컴퓨팅에서 게이트는 금속-산화물-실리콘(MOS) 기반의 트랜지스터로 구성됩니다. 각 게이트는 AND, OR, XOR 등 여러 연산 중 하나에 해당하며, 이 연산들이 함께 작동하여 프로그램을 실행합니다.
기타 조건이 동일할 경우, 제로노울리지 컴퓨팅은 범용 컴퓨팅보다 훨씬 비쌉니다. 예를 들어, Groth16을 사용해 10KB 데이터를 SHA2 해싱하는 데는 140초가 걸리는 반면, 제로노울리지를 사용하지 않으면 단지 몇 밀리초밖에 걸리지 않습니다. 그 이유는 ZK 연산이 각 연산자에 대해 복잡한 산술 연산을 필요로 하기 때문입니다.
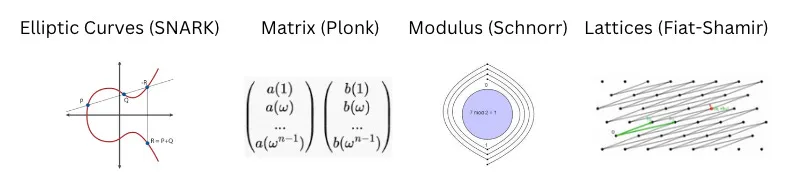
제로노울리지 컴퓨팅에서 연산자는 유한체(finite field)로 표현됩니다. SNARK의 경우, 각 연산자는 타원 곡선 상에서 이루어집니다. 다른 형태의 ZK에서는 행렬, 격자(lattice), 또는 모듈러(modular) 구조를 사용하는데, 이 역시 복잡한 수학적 구조로서 산술 연산을 수행합니다. 이러한 구조를 이용한 간단한 덧셈, 뺄셈, 곱셈조차 매우 비용이 큽니다. 입력 데이터는 숫자가 아닌 유한체로 변환됩니다. 이러한 구조의 복잡성이 암호화 기술의 보안성을 제공하는 기반이 됩니다. 산술 세부사항은 본문의 범위를 넘지만 핵심은, 물리적 회로에서 논리 게이트가 동작하듯이, 제로노울리지의 논리도 소프트웨어 회로 내에서 실행된다는 점입니다.
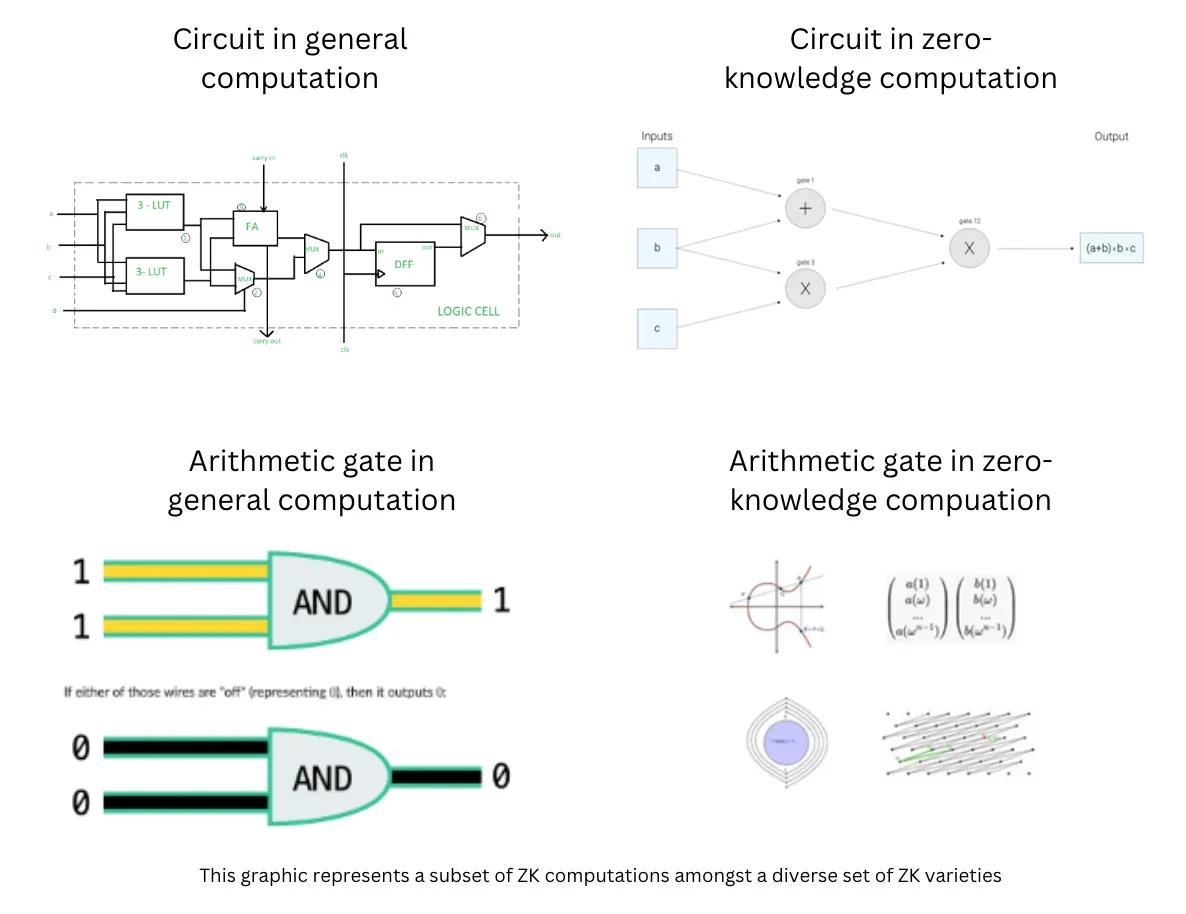
따라서 범용 컴퓨팅의 성능 향상은 물리 법칙에 의해 결정되지만, 제로노울리지 컴퓨팅의 성능 향상은 수학적 법칙에 의해 좌우됩니다. 따라서 하드웨어 가속도 중요한 성능 향상을 가져오지만, 제로노울리지에 무어의 법칙을 적용할 때는 하드웨어보다는 소프트웨어 영역에 초점을 맞춰야 한다는 것을 알 수 있습니다. 이러한 원리를 바탕으로, 제로노울리지에 특화된 무어의 법칙의 형태를 도출할 수 있습니다.
제로노울리지의 돌파구는 불연속적이다
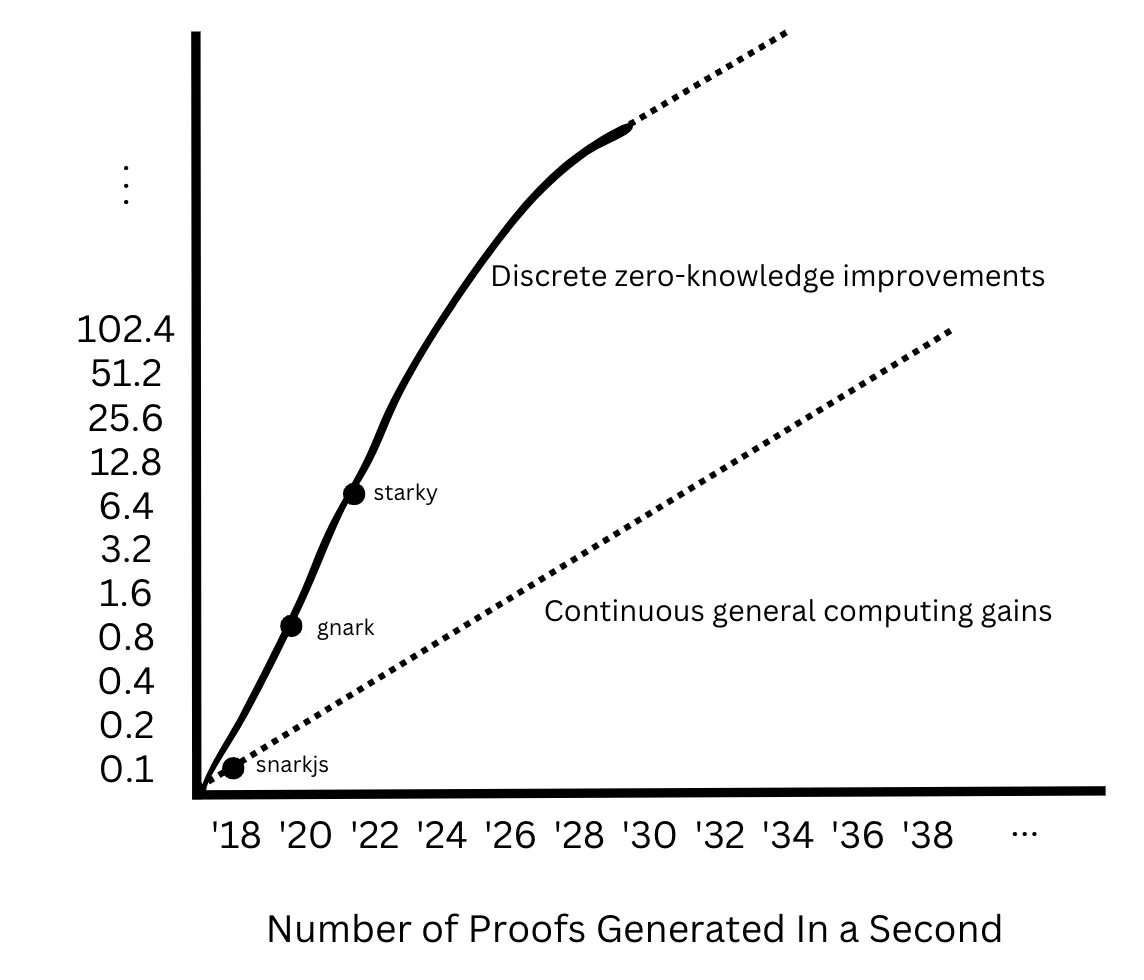
가장 중요한 관찰 중 하나는, 범용 컴퓨팅의 개선이 연속적이지만 제로노울리지 컴퓨팅의 개선은 불연속적이라는 점입니다.
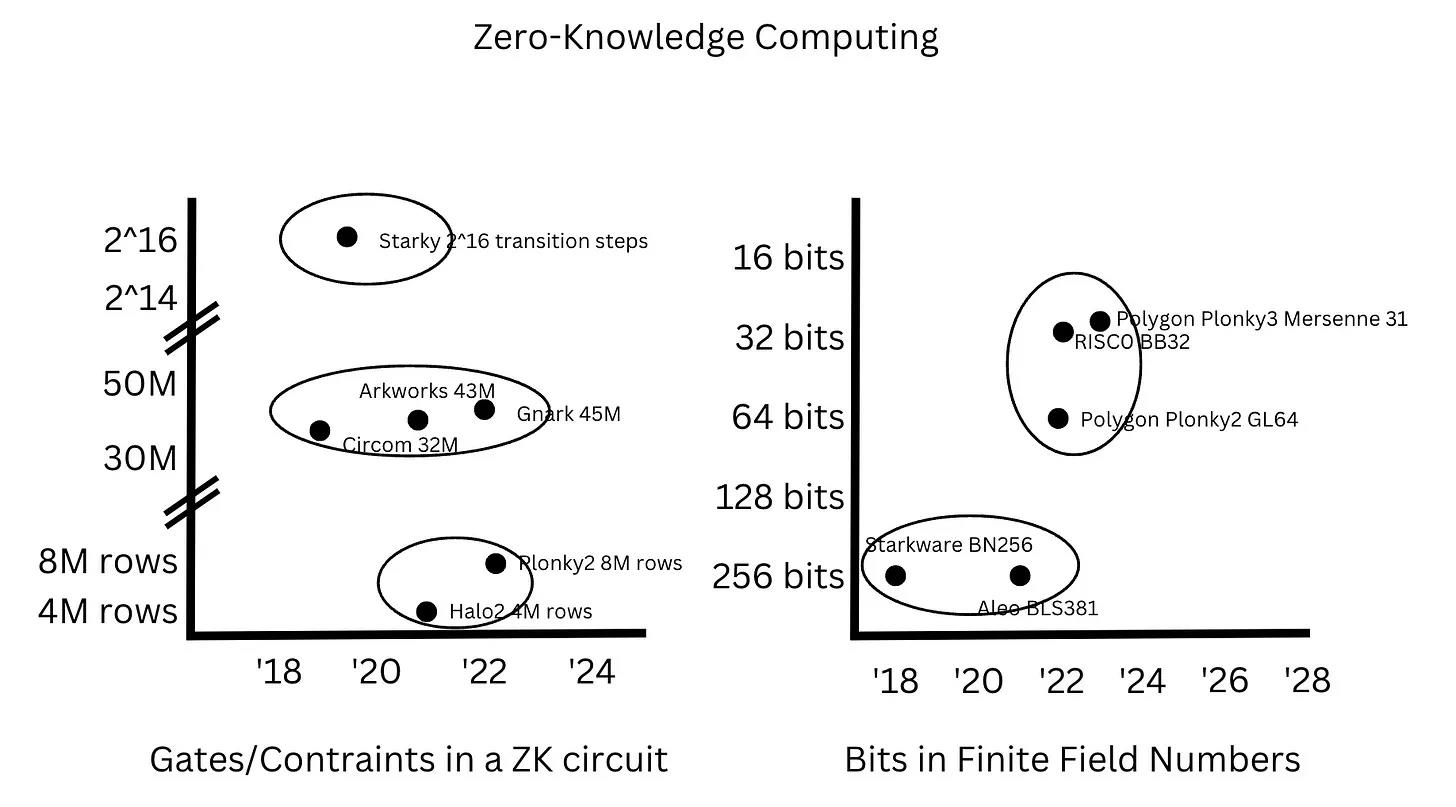
예를 들어, 2005년부터 2020년까지 CPU 코어 수는 대략 5년마다 두 배씩 증가했으며, 클럭 주파수 역시 1990년대부터 2010년대까지 약 5년마다 두 배씩 증가했습니다. 반면 ZK 회로의 제약 조건(constraints) 수는 연속적으로 "향상"되지 않았습니다. SNARKs의 3000~4000만 제약에서 PLONKs의 400~800만 줄로, 이후 STARKs의 2^14~2^16 단계 전이로 점프했습니다. 마찬가지로 유한체의 비트 수는 2018년부터 2022년까지 약 256비트였다가, 2022년부터 2023년 사이에 32비트로 점프하여 32비트 레지스터의 장점을 활용하게 되었습니다.
또한 HyperSpartan의 최신 개발은 R1CS, Plonkish, AIR을 추가 비용 없이 동시에 포괄할 수 있는 커스터마이징 가능한 제약 시스템(CCS)을 지원합니다. SuperNova의 등장은 Nova를 기반으로 하는데, Nova는 다양한 명령어 세트와 제약 시스템과 호환되는 고속 재귀 증명 시스템입니다. 이러한 발전들은 ZK 아키텍처 설계 공간을 더욱 확장하고 있습니다.
이러한 발견을 바탕으로, 제로노울리지의 핵심적인 무어의 법칙은 단일한 연속적 개선 요소에 기반하지 않고, 불연속적인 개선에 의해 주도되는 종합적 성능 향상, 즉 특정 시간 내 생성 가능한 증명 수에 기반합니다. 저는 제로노울리지의 무어의 법칙이 기본 범용 컴퓨팅의 성능 향상을 따라잡기 전까지는 불연속적인 혁명적 점프를 반복할 것이라 생각합니다:
앞으로 몇 년 안에 초당 생성되는 증명 수가 두 배 이상 증가하다가, 점차적으로 기본적인 범용 컴퓨팅 성능 향상과 수렴할 것이다.
제로노울리지 증명 비용 절감
앞서 언급했듯이, 현재 제로노울리지 증명은 광범위한 잠재적 응용을 위해서는 여전히 취약하고 비쌉니다. 특히 검증 비용이 증명 생성 비용을 훨씬 초과합니다. 대략적인 추정에 따르면, ZK 증명 생성 비용은 1달러 미만입니다. 그 이유는 1) 아마존 AWS에서 16코어 CPU와 32GB 메모리를 가진 EC2 인스턴스는 시간당 0.4달러이며, 분산 컴퓨팅 노드는 그보다 더 저렴할 것으로 예상되기 때문이고, 2) Polygon Hermez의 경우 시간당 4~6달러의 비용으로 약 20개의 증명을 생성하기 때문입니다.
그러나 체인 상의 검증 비용은 여전히 매우 높아, 검증 한 번에 23만에서 500만 가스가 소모되며, 이는 약 100~2000달러에 해당합니다. ZK 롤업은 수천 건의 거래에 걸쳐 비용을 분산함으로써 규모의 경제를 누릴 수 있지만, 다른 유형의 ZK 애플리케이션은 앞서 언급한 애플리케이션 레이어 혁신을 실현하고 궁극적으로 사용자 삶의 질을 향상시키기 위해 검증 비용을 낮추는 방법을 찾아야 합니다.
제로노울리지 증명 용량의 돌파구가 불연속적이고 이산적인 단계로 발생할 가능성이 있으므로, 이러한 돌파구가 발생할 수 있는 잠재적 영역을 살펴보겠습니다. 아래는 zkprize에서 제시한 일부 최적화 방법들입니다:
-
알고리즘 최적화: 다중 스칼라 곱셈(MSM)과 수론 변환(NTT) 등 타원 곡선 암호화를 가속화하는 알고리즘들이 있으며, 이들은 자체적으로 하드웨어 가속이 가능합니다. 푸리에 변환은 NTT의 한 예로, 다양한 구현체에서 이미 최적화되었습니다.
-
병렬 처리: 데이터 구조의 사전 처리, 회로 평가, 증명 생성 부분을 여러 처리 장치 또는 멀티스레드에 위임함으로써 ZK 처리량을 증가시킬 수 있습니다.
-
컴파일러 최적화: 레지스터 할당, 루프 최적화, 메모리 최적화, 명령어 스케줄링 등을 개선할 수 있습니다.
알고리즘 최적화 측면에서는, SNARK의 R1CS에서 Halo2, Plonky2, HyperPlonk의 Plonkish로의 산술화 전환이 있으며, 이는 Starky 증명에서 사용되는 AIR과도 다릅니다. 또한 접기(folding) 방식의 최신 발전은 흥미롭습니다. HyperNova는 커스터마이징 가능한 제약 시스템을 지원하여 점진적 검증 가능한 연산을 가능하게 합니다. 병렬 처리 측면에서는 Polygon 팀이 발표한 Plonky2의 재귀적 확장이 병렬 증명 생성 가능성을 크게 넓혔습니다. 컴파일러 최적화 측면에서는 제로노울리지용 LLVM 사용이 매우 흥미롭습니다. IR(중간 표현)이 명령어 세트에 독립적인 오퍼코드로 컴파일될 수 있기 때문입니다. 예를 들어 Nil Foundation의 ZK-LLVM이나 Risc0의 zkVM도 LLVM을 사용하여 각 단계 실행 추적을 위한 제로노울리지 증명을 생성합니다. 일반적인 ZKVM 또는 LLVM은 블록체인 외부의 다양한 사용 사례로 ZK를 확장할 뿐 아니라, 개발자가 코드 이식성을 높이고 쉽게 참여할 수 있도록 합니다.
제로노울리지 개발자에게 미치는 영향
범용 컴퓨팅에서는 가치 축적이 기존 사업자에게 유리하게 작용합니다. 예를 들어, 칩 제조사는 점점 더 작은 칩 생산 기술을 개선하기 위한 자본 투자라는 진입 장벽을 형성하며 이익을 얻습니다. 그러나 제로노울리지의 혁신은 불연속적인 혁명적 점프로 이루어지기 때문에, 새로운 팀들도 연구 중심의 기술적 돌파를 통해 새로운 증명 시스템을 발명함으로써 기존 사업자를 뛰어넘을 기회가 충분히 있습니다.
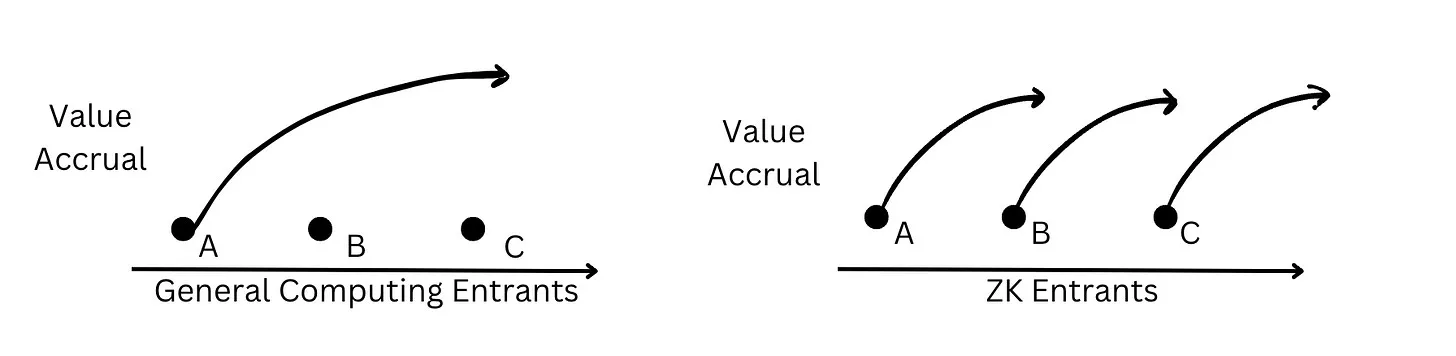
이 이론을 바탕으로 Web3 제로노울리지 개발자들에게 다음과 같은 시사점이 있습니다:
-
제로노울리지 개발자는 모듈화 설계를 고려해야 합니다. ZK 회로를 사용하는 프로토콜 개발자는 최첨단 ZK 기술 구성 요소를 교체할 수 있도록 모듈화 설계를 고려해야 합니다.
-
참여자들은 연구 중심의 파괴적 혁신에서 이익을 얻을 수 있습니다. 연구 역량을 갖춘 팀은 혁신적인 새로운 증명 시스템을 제안하거나 선도적으로 구현함으로써 기존 팀을 앞서갈 수 있습니다.
-
수직 통합 기업은 최신 기술 조합을 통해 이익을 얻을 수 있습니다. 하드웨어에서 컴파일러, 회로에 이르는 ZK 스택의 각 계층이 자체적으로 개선될 수 있기 때문에, 수직 통합 기업은 최신 기술을 모듈화하여 가장 낮은 비용으로 애플리케이션 개발팀에게 최첨단 ZK 기술을 제공할 수 있습니다.
이러한 관점에서 저는 업계 전반에 걸쳐 다음과 같은 세 가지 주요 발전이 나타날 것이라 예상합니다:
-
새로운 팀들이 기술적 돌파로 기존 ZK 프로토콜을 추월한다.
-
기존 프로토콜들은 기술이 아닌 생태계를 기반으로 한 경쟁 우위를 추구한다.
-
수직 통합된 ZK 제공업체가 등장하여 낮은 비용으로 최신 기술을 제공한다. 이 빠르게 변화하는 분야에서는 혁신과 파괴가 계속해서 발생할 것이다.
결론
기술의 역설은 기술이 잘 작동할수록 오히려 보이지 않는다는 점입니다. 우리는 물을 마실 때 유리잔을 의식하지 않으며, 이메일을 보낼 때 컴퓨터 칩을 인식하지 못합니다. 목표가 더 쉬워질수록 우리는 과정을 더 쉽게 무시하게 됩니다.
제로노울리지 증명은 이미 사용자 경험을 향상시키는 확장 가능한 애플리케이션을 제공할 가능성이 큽니다. 기술이 잘 작동하면 우리는 증명의 존재를 인식하지 못하지만, 거래가 더욱 사생활 보호되고, 정보가 더 정확하며, 롤업이 더 빠르고 저렴해지는 것을 느낄 것입니다. 따라서 제로노울리지 증명은 결국 트랜지스터, 마이크로칩, 그리고 오늘날의 인공지능처럼 우리 삶의 기반이 될 수 있습니다.
선거에서 부정행위를 막는 방법, 금융 시스템의 중개자 제거를 통해 거래 비용을 절감하는 방법, 또는 ZK 기반 분산 컴퓨팅으로 AI 훈련을 민주화하는 방법을 굳이 고민할 필요가 없습니다. 언젠가 우리가 무어의 관찰인 “회로 기판의 트랜지스터 수는 18~24개월마다 두 배로 증가한다”를 일종의 ‘법칙’으로 받아들였듯이, “초당 제로노울리지 증명 수는 매년 지수적으로 증가한다”는 사실을 당연하게 여기며 그 혁신의 혜택을 누리게 될지도 모릅니다. 목표 달성이 더 쉬워지고, 누구도 더 이상 제로노울리지를 칭송하지 않으며, 우리는 일상적인 삶을 계속 살아가게 될 것입니다.
TechFlow 공식 커뮤니티에 오신 것을 환영합니다
Telegram 구독 그룹:https://t.me/TechFlowDaily
트위터 공식 계정:https://x.com/TechFlowPost
트위터 영어 계정:https://x.com/BlockFlow_News











