
비탈릭: 프로토콜 설계에서의 캡슐화된 복잡성과 시스템적 복잡성
글: 비탈릭 부테린, 이더리움 공동 창시자
번역: 남풍, Unitimes
이더리움 프로토콜 설계의 주요 목표 중 하나는 복잡성을 최소화하는 것이다. 블록체인이 효과적인 블록체인 네트워크로서 수행해야 할 일을 계속 수행하면서도 가능한 한 간단하게 프로토콜을 만드는 것이다. TechFlow
그러나 이 목표에는 난관이 있다. 바로 복잡성이란 개념 자체가 정의하기 어렵다는 점이며, 때때로 서로 다른 유형의 복잡성과 각기 다른 대가를 지닌 선택지 사이에서 균형을 잡아야 하는 상황이 발생한다. 우리는 어떻게 비교해야 할까?
복잡성에 대해 더 섬세하게 사고할 수 있게 해주는 강력한 도구가 있는데, 바로 우리가 말하는 캡슐화된 복잡성(encapsulated complexity)과 시스템적 복잡성(systemic complexity)을 구분하는 것이다.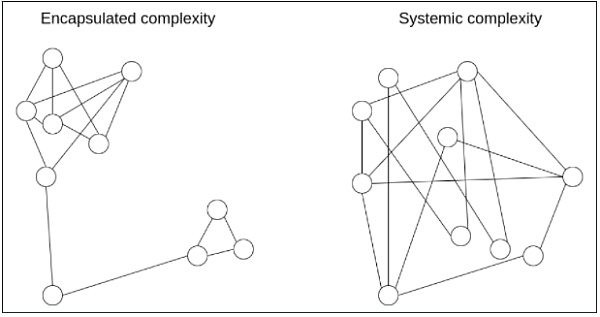
서브시스템 내부는 복잡하지만 외부에는 단순한 인터페이스(interface)만을 제공할 때, 이를 '캡슐화된 복잡성'이라고 한다. 반면 시스템의 구성 요소들이 명확히 분리되지 않고 서로 복잡하게 얽혀 있을 때는 '시스템적 복잡성'이 발생한다.
다음은 몇 가지 예시들이다.
BLS 서명 vs. 슈노르(Schnorr) 서명
BLS 서명과 슈노르 서명은 타원 곡선 기반으로 구현되는 두 가지 일반적인 암호 서명 방식이다.
BLS 서명은 수학적으로 매우 단순해 보인다:
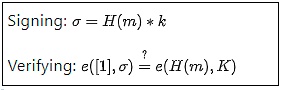
H는 해시 함수이고, m은 메시지이며, k와 K는 각각 개인키와 공개키이다. 지금까지는 간단하다. 그러나 진정한 복잡성은 e 함수 안에 숨어 있다. 즉, 타원 곡선 페어링(elliptic curve pairings)인데, 이는 암호학 전체에서도 가장 이해하기 어려운 수학적 개념 중 하나이다.
이제 슈노르 서명을 살펴보자. 슈노르 서명은 기본적인 타원 곡선만을 사용한다. 하지만 서명 및 검증 로직은 다소 복잡하다:

그렇다면 어떤 서명 방식이 "더 단순할까"? 그것은 당신이 무엇을 중요하게 여기느냐에 달려 있다! BLS 서명은 엄청난 기술적 복잡성을 가지고 있지만, 그 복잡성은 e 함수 정의 속에 모두 감춰져 있다. 만약 e 함수를 블랙박스로 본다면, BLS 서명은 실제로 매우 단순하다. 반면 슈노르 서명은 전체적인 복잡성은 낮지만, 외부 세계와 미묘하게 상호작용하는 부분이 더 많다.
예를 들어:
-
BLS 다중 서명(두 개의 키 k1과 k2 결합)은 매우 간단하다: 그냥 σ1+σ2 하면 된다. 그러나 슈노르 다중 서명은 2단계의 상호작용을 필요로 하며, 까다로운 키 취소(Key Cancellation) 공격 문제도 처리해야 한다.
-
슈노르 서명은 난수 생성이 필요하지만, BLS 서명은 그렇지 않다.
타원 곡선 페어링은 종종 강력한 '복잡성 스폰지(sponge)' 역할을 하는데, 이는 많은 캡슐화된 복잡성을 포함하고 있으면서도 해결책의 시스템적 복잡성은 줄여주기 때문이다. 이는 다항식 커밋(polynomial commitments) 영역에도 적용된다. 페어링을 요구하는 KZG 커밋의 단순함과 페어링 없이 작동하는 내적 증명(inner product arguments)의 더 복잡한 내부 논리를 비교해볼 수 있다.
암호학 vs. 암호경제학
많은 블록체인 설계에서 중요한 설계 선택은 암호학(cryptography)과 암호경제학(cryptoeconomics) 사이의 균형이다. (예: 롤업에서) 이것은 종종 유효성 증명(즉, ZK-SNARKs)과 사기 증명(fraud proofs) 사이의 선택으로 나타난다.
ZK-SNARKs는 기술적으로 복잡하다. ZK-SNARKs의 작동 원리는 한 편의 글로 설명할 수 있지만, 실제 계산을 검증하기 위해 ZK-SNARK을 구현하는 것은 원래 계산보다 훨씬 더 많은 복잡성을 요구한다. (그래서 EVM용 ZK-SNARK 증명은 아직 개발 중인 반면, EVM용 사기 증명은 이미 테스트 단계에 있다.) 효율적인 ZK-SNARK 증명을 구현하려면 특수 목적에 맞게 최적화된 회로 설계, 낯선 프로그래밍 언어 사용 등 다양한 도전 과제가 따른다. 반면 사기 증명은 본질적으로 간단하다: 누군가 도전하면 체인 상에서 해당 계산을 직접 실행하면 된다. 효율성을 높이기 위해 이진 탐색 방식을 추가하기도 하지만, 그렇다고 해서 복잡성이 크게 늘어나지는 않는다.
ZK-SNARKs는 복잡하지만, 그 복잡성은 캡슐화된 복잡성이다. 반면 사기 증명의 상대적으로 낮은 복잡성은 시스템적 복잡성이다. 다음은 사기 증명이 유발하는 시스템적 복잡성의 예시들이다:
-
검증자의 딜레마를 피하기 위해 신중한 인센티브 설계가 필요하다.
-
합의 과정에서 완료된다면, 사기 증명을 위한 추가 트랜잭션 유형을 제공해야 하며, 여러 참여자가 동시에 사기 증명을 제출하려 할 경우를 고려해야 한다.
-
동기화된 네트워크에 의존한다.
-
검열 공격(censorship attacks)이 도난 수단으로 악용될 수 있다.
-
사기 증명 기반 롤업은 즉시 인출을 지원하기 위해 유동성 제공자가 필요하다.
이러한 이유들 때문에, 복잡성 측면에서도 ZK-SNARK 기반 순수 암호학적 해결책이 장기적으로 더 안전할 수 있다. ZK-SNARKs는 더 복잡한 부분이 존재하며, 이는 일부 사람이 ZK-SNARKs를 선택할 때 고려해야 할 요소이다. 그러나 ZK-SNARKs는 누구나 고려해야 할 '잔여 경고 사항'이 적다.
다양한 예시들
-
PoW(나카모토 합의): 메커니즘이 매우 단순하고 이해하기 쉬우므로 캡슐화된 복잡성은 낮지만, 자가 마이닝(자기 이익 추구 마이닝) 공격 등으로 인해 시스템적 복잡성은 더 높다.
-
해시 함수: 캡슐화된 복잡성은 높지만, 속성이 매우 명확하여 시스템적 복잡성은 낮다.
-
무작위 셔플 알고리즘: 셔플 알고리즘은 내부적으로 복잡할 수 있으며(예: Whisk), 강력한 무작위성을 보장하면서도 이해하기 쉬울 수 있다. 또는 내부적으로 단순하지만 약하고 분석하기 어려운 무작위성 속성을 만들어낼 수도 있다(즉, 시스템적 복잡성).
-
채굴자 가치 추출(MEV): 복잡한 트랜잭션(complex transactions)을 지원할 만큼 강력한 프로토콜은 내부적으로 매우 단순할 수 있지만, 이러한 복잡한 트랜잭션이 블록 제안 방식을 매우 비정상적으로 만들면서 프로토콜의 인센티브 메커니즘에 복잡한 시스템적 영향을 미칠 수 있다.
-
Verkle 트리: Verkle 트리는 확실히 일정한 캡슐화된 복잡성을 가지고 있으며, 실제로 일반적인 Merkle 해시 트리보다 훨씬 더 복잡하다. 그러나 시스템적으로 보면, Verkle 트리는 키-값(key-value) 매핑과 동일한 깔끔하고 단순한 인터페이스를 제공한다. 주요한 시스템적 복잡성 "누수(leak)"는 공격자가 특정 값을 매우 긴 분기(branch)를 갖도록 Verkle 트리를 조작할 가능성이다. 그러나 Verkle 트리와 Merkle 트리의 위험은 동일하다.
어떻게 균형을 잡아야 할까?
일반적으로 캡슐화된 복잡성이 낮은 선택이 시스템적 복잡성도 낮기 때문에, 더 단순한 선택이 명확한 경우가 많다. 그러나 때로는 한 유형의 복잡성과 다른 유형의 복잡성 사이에서 어려운 결정을 내려야 한다. 이 지점에서 분명한 것은 캡슐화된 복잡성이 위험성이 더 낮다는 것이다. 시스템적 복잡성으로 인한 위험은 단순히 사양(specification)의 길이 함수가 아니다. 10행 코드의 작은 조각이 다른 부분들과 상호작용하면서, 100행 함수보다 더 복잡해질 수 있으며, 후자는 블랙박스로 간주될 수 있다.
그러나 캡슐화된 복잡성을 선호하는 접근법에는 한계가 있다. 어떤 코드 조각이라도 소프트웨어 버그가 발생할 수 있으며, 코드가 커질수록 오류 발생 확률은 1에 가까워진다. 때때로 예상치 못한 새로운 방식으로 서브시스템과 상호작용해야 할 때 처음의 캡슐화된 복잡성이 시스템적 복잡성으로 전환될 수 있다.
후자의 예로는 현재 이더리움의 2단계 상태 트리(two-level state tree)가 있다. 이 구조는 계정 객체 트리로 구성되며, 각 계정 객체는 자체 저장 트리를 가진다.
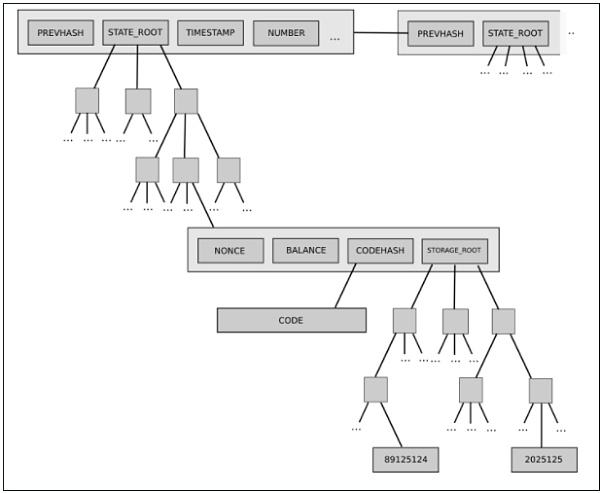
이 트리 구조는 복잡하지만, 처음에는 이런 복잡성이 잘 캡슐화된 것으로 보였다. 프로토콜의 나머지 부분은 키/값 저장소처럼 트리와 상호작용했으므로, 트리가 어떻게 구성되었는지는 신경 쓸 필요가 없었다.
그러나 이후 이 복잡성이 시스템적 영향을 미친다는 것이 밝혀졌다. 각 계정이 임의 크기의 저장 트리를 가질 수 있다는 것은, 특정 상태 부분(예: "0x1234로 시작하는 모든 계정")이 예측 가능한 크기를 가질 것이라는 것을 믿을 수 없다는 의미다. 이는 상태를 여러 부분으로 나누는 것을 더 어렵게 만들며, 동기화 프로토콜 설계 및 저장 프로세스 분산 시도를 더욱 복잡하게 만든다. 왜 캡슐화된 복잡성이 시스템적으로 변했는가? 인터페이스가 바뀌었기 때문이다. 해결책은 무엇인가? 현재 Verkle 트리로의 전환 제안에는 균형 잡힌 단일 계층 트리 설계로의 전환도 포함되어 있다.
결국 어떤 상황에서든 어떤 유형의 복잡성이 더 바람직한지는 간단한 답이 없는 문제이다. 우리가 할 수 있는 최선은 캡슐화된 복잡성을 적절히 선호하되, 너무 지나치지 않고 각 사례마다 판단력을 발휘하는 것이다. 때로는 캡슐화된 복잡성을 크게 줄이기 위해 시스템적 복잡성을 약간 희생하는 것이 최선일 수 있다. 다른 경우에는 어떤 것이 캡슐화된 것인지 아닌지조차 잘못 판단할 수 있다. 모든 경우는 다르다.
TechFlow 공식 커뮤니티에 오신 것을 환영합니다
Telegram 구독 그룹:https://t.me/TechFlowDaily
트위터 공식 계정:https://x.com/TechFlowPost
트위터 영어 계정:https://x.com/BlockFlow_News
















