Vitalik：探索橢圓曲線配對

撰文：Vitalik Buterin

發表時間：2017 年 1 月 14 日

密碼學的眾多基礎建設，例如「確定性閾值簽名」 (deterministic threshold signature，暫譯)、zk-SNARKs 與其他形式較簡單的零知識證明等等，背後關鍵的原始模型之一是橢圓曲線對。橢圓曲線在三十餘年來廣泛使用於加密、數位簽章等密碼學應用，「橢圓曲線對(EC pairings)」（或雙線性映射）是最近基於其上的新玩意，它引進了加密乘法，讓基於橢圓曲線的協定，所能做的事情大為增加。這篇文章會詳細地介紹橢圓曲線對，以及簡要解釋它如何運作。

因為這概念真的不容易，不太預期你讀第一遍甚至是第十遍時就真的完全理解，但希望這篇文章能至少告訴你一些箇中奧妙。

橢圓曲線本身就已經是一個不太容易理解的主題，但這篇文章大多時候會假設你對它的運作原理有些認識，如果你沒有基本概念的話，我會推薦這篇文章作為入門。

總的來說，橢圓曲線處理的是一些稱為「點(points)」的數學物件，直白說是二維平面上的點(x, y)，以及一些加減運算的特別公式（例如計算R = P + Q），你還可以讓點去乘以一個整數（例如P * n = P + P + … + P，雖然說在n 很大的時候有個快得多的算法）。

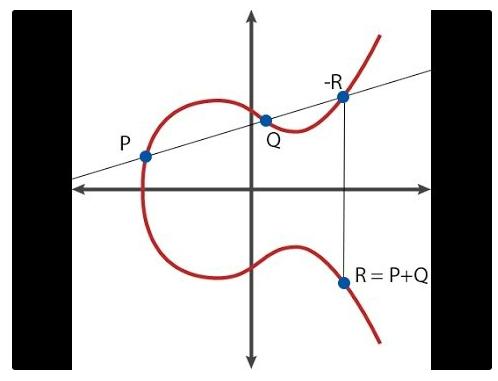
這是點的加法在圖上看起來的樣子

除此之外有個特別的點叫做「無窮遠點」(O)，在點的運算規則中作為零元素，也就是對於所有點都有P + O = P。一條曲線還擁有一個稱為「階(order)」的特質，也就是存在一個正整數n，對於所有P 都使得P * n = O（當然P * (n + 1) = P，P * ((7*n) + 5) = P * 5，以此類推）。還有某個事先協議好的「生成點(generator point) G」，也就是挑選來作為加法單位元素、代表數字1 那個角色的點。理論上任何曲線上的點都可以當生成元，重要的是那個G 是統一選定的。

配對就是進一步允許你驗證某類更復雜的等式：例如，如果P = G * p、Q = G * q、R = G * r，當你要檢查p * q = r 是否成立，你只要有P, Q, R 三個點的座標做為輸入就行了。這也許看起來像是橢圓曲線最基本的安全保證被打破了，因為乍看之下，要是知道P 點的座標就洩漏了p 的值。但事實上這樣洩漏的風險非常侷限──準確來說，判定性的 Diffie-Hellman 問題很容易，但是計算性的版本仍然是「計算上不可行(computationally infeasible)」的。至少難度就跟不知道這個值差不多。

第三種理解「配對」的方式，也許是在我們討論的大部分使用情境裡最有啟發性的方式是，如果你把橢圓曲線上的點看成一個單向加密函數（也就是說encrypt(p) = p * G = P），那麼對比傳統橢圓曲線的數學原理讓你檢驗變數間的線性約束（例如P = G * p、Q = G * q、R = G * r，檢驗5 * P + 7 * Q = 11 * R 其實是在檢驗5 * p + 7 * q = 11 * r），橢圓曲線對就是讓你檢驗變數間的二次約束（檢驗e(P, Q) * e(G, G * 5) = 1 其實是在檢驗p * q + 5 = 0）。能夠做到二次以後，就足夠讓我們做些像是確定性閾值簽名、QAP (quadratic arithmetic programs，一種零知識證明) 等等有趣的應用。

現在的問題是我們上面引進的e(P, Q) 這個運算子到底是什麼？這就是一組「配對」。數學家們有時候也把它叫做「雙線性映射」，「雙線性」在這裡基本上表示它滿足以下條件：

e(P, Q + R) = e(P, Q) * e(P, R)
e(P + S, Q) = e(P, Q) * e(S, Q)

注意到這裡的+ 和* 可以是任意的運算子；當你新建立一類數學物件的時候，抽象代數上不在意+ 和* 是如何被「定義」的，只要和我們習以為常的運算一致就可以了，像是a + b = b + a、(a * b) * c = a * (b * c)、(a * c) + (b * c) = (a + b) * c。

假如現在P, Q, R, S 僅僅是數字，那配對函數十分容易構造：我們可以定義e(x, y) = 2^(xy)。那麼我們就會看到：

e(3, 4 + 5) = 2^(3 * 9) = 2²⁷
e(3, 4) * e(3, 5) = 2^(3 * 4) * 2^(3 * 5) = 2¹² * 2¹⁵ = 2²⁷

它確實是雙線性的！

然而像這樣簡單的配對不適合用在密碼學上，因為要分析單純運作在整數上的數學物件簡直輕而易舉；整數的性質使得除法、對數等等許多操作變得容易。整數也沒有「公鑰」或是「單向函數」的概念。進一步說，上面描述的那種配對是可逆的：知道x、知道e(x, y)，做個除法和對數就可以算出y。我們想要的數學結構是儘可能接近「黑盒子」：你可以做些加減乘除，但也就只能這樣了。這個時候橢圓曲線和橢圓曲線對就派上用場了。

人們發現，確實能在橢圓曲線的點上設計雙線性映射──也就是當輸入是橢圓曲線上的兩個點P 和Q，構造一個函數e(P, Q) 映射到一個F_p¹² 的元素（至少在這個特定情形下夠用了，而這規範根據曲線的細節會有所不同，後面會再提到），但做到這件事情底下的數學實在是十分複雜。

第一，我們來介紹質數體(prime fields) 和擴體(extension fields)。上圖畫的曲線雖然漂亮，但那是在你假設曲線的等式定義在平常所用的實數上才會長成那樣。如果我們真的在密碼學裡使用實數，那你就可以用對數「倒回去」，那一切就沒用了，更何況儲存實數所需的空間可能會無盡地長。因此，我們改用實數體上的數字。

一個質數體由數字0, 1, 2, …, (p−1) 所成集合構成，其中p 是一個質數，而其運算由下定義：

a + b: (a + b) % p 
a * b: (a * b) % p 
a - b: (a - b) % p 
a / b: (a * b^(p-2)) % p

基本上，所有運算都在模(modulo) p 下進行（這裡有模運算的簡介)。除法是個特例。一般來說，3/2 不是整數，但我們想要只處理整數，所以我們改成去找整數x 使得x * 2 = 3，而這裡的* 當然是指上面定義的模數乘法。幸虧有費馬小定理，除法的那個指數定義能滿足需要，但還有個更快的做法，那就是用擴展歐幾里得演算法。假設p = 7，下面有幾個例子：

2 + 3 = 5 % 7 = 5 
4 + 6 = 10 % 7 = 3 
2 - 5 = -3 % 7 = 4 
6 * 3 = 18 % 7 = 4 
3 / 2 = (3 * 2^5) % 7 = 5 
5 * 2 = 10 % 7 = 3

如果你試著操作這樣的運算，你會發現它是前後一致的，而且滿足所有尋常的規則。最後的兩個例子說明(a / b) * b = a，你還可以發現(a + b) + c = a + (b + c)、(a + b) * c = a * c + b * c，還有其他你高中所知道和喜愛的代數等式都還會繼續運作。現實上使用的橢圓曲線，點和等式通常都是在質數體上運算的。

現在我們來談談擴體。你先前可能已經看過擴體了，數學課本上最常遇到的例子是複數體──以實數體為基礎加入 sqrt(-1) = i 這個新的元素後擴張而成的。簡單來說，擴體就是在一個現成的體上，「發明」一個新的元素，並且定義好這個新元素跟現有的元素的關係（在剛剛的例子裡的話是i^2 + 1 = 0) ；這個關係式不能被現有的數字滿足，那把這個新元素加進「舊有的元素的所有線性組合( linear combination )」組成的集合便是構造出來的集合。

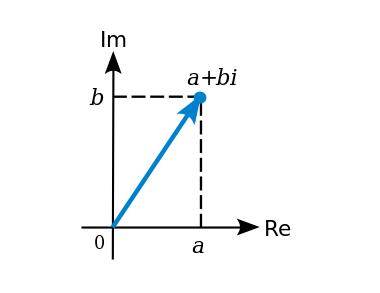
我們也可以對質數體進行擴張；舉個例子，在模7 的質數體里加入我們剛剛所說的i，那麼我們有

(2 + 3i) + (4 + 2i) = 6 + 5i 
(5 + 2i) + 3 = 1 + 2i 
(6 + 2i) * 2 = 5 + 4i 
4i * (2 + i) = 3 + i

最後的等式可能比較難以理解；其實那條等式的第一步是先把左邊的乘法做分配變成4i * 2 + 4i * i，得到8i - 4。因為我們是在模7 的環境下做運算，這個數字就變成了i + 3。至於除法的部份則是：

a / b : (a * b^(p^2-2)) % p

這邊費馬小定理的指數從p 變成了p² ，當然也可以使用擴展歐幾里得演算法來更有效率地運算。因為對於在體中的任一個元素x 都會有x ^ (p² − 1) = 1 ，所以我們稱(p² − 1) 為「體中乘法群的階」。

對於實數體，代數基本定理保證了它的二次擴體(quadratic extension) ：複數體，是完備的（譯者注：應為代數封閉，實數體亦具有完備性但可以擴張）──這個體不能再被擴張，因為所有可能的新元素j 與現有的複數之間應該要滿足的數學關係（嚴格來講是以多項式來定義的數學關係），都有一個在體內的元素早已滿足。但在質數體中，就沒有這個問題，我們可以對其進行三次擴張(cubic extension)（新元素w 與現有元素的關係式是一條三次多項式，因此1, w , w² 是線性獨立(linear independent) 的），高次擴張，甚至擴張再擴張等等。橢圓曲線就是建立在這些模運算的複數上的。

對這些數學如何實作成程式碼有興趣的話，這邊有一些實作質數體以及擴體的例子。

回頭來看橢圓曲線對。橢圓曲線對（我們這邊討論的配對只是其中一種，但配對的邏輯是相近的）是一個G2 × G1 → Gt 的映射，其中：

• G1是一條橢圓曲線，線上的點滿足形如y² = x³ + b 的式子，而且點的x, y 座標都是F_p 的元素（也就是說他們只是普通的數字，但算術運算會在模某個質數下進行）。
• G2也是一條橢圓曲線，同樣滿足G1 的曲線，但G2 中的元素的x, y座標是F_p¹² 的元素（這是我們剛才講到的那些複數；我們定義一個神奇數字w，它滿足一個12 次多項式w¹² − 18 w⁶ + 82 = 0）
• Gt是橢圓曲線的運算結果形成的集合。在我們討論的曲線中，Gt 是F_p¹²（跟G2 用一樣的那些複數）

它主要必須滿足的性質是雙線性，在這個脈絡下這樣代表：

e(P, Q + R) = e(P, Q) * e(P, R)
e(P + Q, R) = e(P, R) * e(Q, R)

（譯者注：這邊的雙線性準確來說是「整數上的雙線性(bilinearity over ℤ)」，只是因為這裡所討論的橢圓曲線上的點都是整數點，而且乘法和加法的定義是整數運算完再取模，自然已經滿足一些線性性質）

選擇配對函數還有兩個重要的準則：

• 運算要足夠有效率（例如我們可以直接對所有點取離散對數然後全部乘起來，作為一種簡單的配對方法，但這所需要的運算成本和破解橢圓曲線密碼學一樣困難，所以這不算）
• 非退化（你當然可以單純地定義e(P, Q) = 1，但它並不是一個特別有用的配對）

所以我們該怎麼做到這件事？

讓配對函數得以運作背後的數學十分困難，而且需要一些進階的代數，超過我們目前為止所見，但我會大致說明。首先我們需要定義「因子(divisor)」的概念，基本上是另一種方式來表示作用在橢圓曲線上的點的函數們。一個函數的因子基本上計算了一個函數有多少個零點和取值無限大的點。為了理解清楚一些，我們來看看幾個例子。讓我們選定一個點P = (P_x, P_y)，然後考慮以下函數：

f(x, y) = x − P_x

它的因子是[P] + [−P] − 2 * [O] （這裡的方括號用來表示某個點出現在函數的零點和取值無限大的點所成集合，而不是那個點本身；[P] + [Q] 和[P + Q]並不相同）。原因如下：

• 這個函數在P 點的值等於零，因為x 取值P_x，所以x − P_x = 0
• 這個函數在−P 點的值等於零，因為−P 和P 的x 座標相同
• 這個函數在x 趨向無限大的時候也趨向無限大，所以我們說這個函數在O 點取值無限大。計算這個無窮遠點要算兩次，所以O 要乘以乘數-2（負號是因為它是無窮遠點而有別於零點，2 是因為它要被算兩次）。

計算上的理由大約是：因為這個曲線的方程式是x³ = y² + b，當x 增加，為了讓y² 達到相當的規模，y 增長的速度大約需要是x 的1.5 倍。因此如果一個線性函數只包含x，那它無限大那一項的乘數是2，但如果它包含y，那乘數就要是3。

現在考慮一條線的函數：

ax + by + c = 0

其中a, b, c 被選定來讓這條線通過點P 和點Q。根據橢圓曲線加法的運作方式，它也一定會通過−P−Q 這個點。因為它跑向無限大時會同時取決於x 和y，所以因子是[P]+ [Q] + [−P−Q] − 3 * [O]。

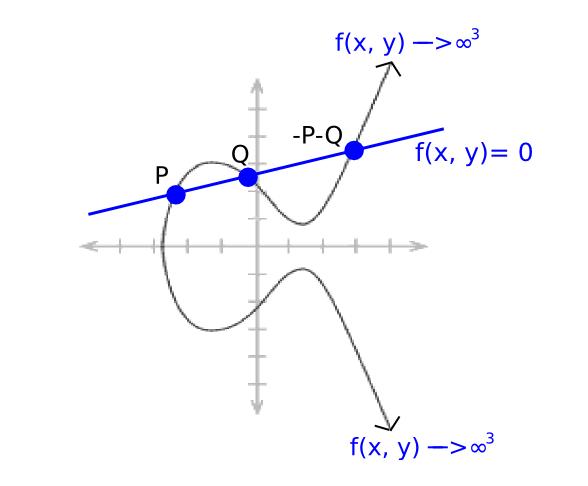
我們知道所有「有理函數」（也就是點座標經過有限次加減乘除運算定義出來的函數）唯一地對應到某個因子，頂多就是多乘一個常數（也就是如果兩個函數F 和G 有相同的因子，那麼必存在常數k 使得F = G * k）。

對於任意兩個函數F 和G，(F * G) 的因子等於F 和G 的因子之和（數學課本上你會看到(F * G) = (F) + (G)），所以比如f(x, y) = P_x − x，那麼(f³) = 3 * [P] + 3 * [−P] − 6 * [O]；P 和−P 算三次是因為在特定的數學意義下f³ 會「三倍快地」靠近0。

留意有個定理說如果你把某個因子的「方括號」拿掉，那些點運算後的結果必定是O（[P] + [Q] + [−P−Q] − 3 * [O] 照著操作會得到P + Q − P − Q − 3 * O = O），而且任何有這個性質的因子就會是那個函數的因子。

現在我們可以開始看Tate pairing 了。考慮以下用因子定義的函數：

• (F_P) = n * [P] − n * [O]，其中n 是G1 的階數，也就是對於所有P，n * P = O
• (F_Q) = n * [Q] − n * [O]
• (g) = [P + Q] − [P] − [Q] + [O]

現在，讓我們看看這個乘積F_P * F_Q * g^n。它的因子是：

n * [P] − n * [O] + n * [Q] − n * [O] + n * [P + Q] − n * [P] − n * [Q] + n * [O]

化簡會得到乾淨的：

n * [P + Q] − n * [O]

注意到這個因子的格式跟F_P 和F_Q 的因子相符。因此有F_P * F_Q * g^n = F_(P + Q)。

現在再多做一個稱為「最終指數(final exponentiation)」的操作，把前述運算的結果（F_P, F_Q 等等）自乘到z = (p¹² − 1) / n 的冪次，其中p¹² − 1 是F_p¹² 中乘法群的階（換句話說就是對於所有x ϵ F_p¹², x^(p¹² − 1) = 1）。注意到如果你把這個指數套用在任何已經是n 次冪的結果上，你就會得到某個元素的(p¹² − 1) 次方，結果就會變成1。因此，在最後的指數步驟後，g^n 會消掉，然後我們就會得到F_P^z * F_Q^z = F_(P + Q)^z。於是就有了雙線性的性質的一部分。

現在如果你想構造一個函數，它在兩個參數上都會是雙線性的，你需要更嚇人的數學，那麼要做的不只是算F_P，還要計算F_P 的因子，再做下去就會得到完整的Tate pairing。為了證明更多結論你需要理解一些概念像是「線性等價(linear equivalence) 」以及Weil reciprocity 之類。這些概念詳細的內容可以在這裡以及這裡看到。

而這邊實作了一個Tate pairing 的修改版── Optimal Ate Pairing。該代碼裡還實現了用米勒算法來計算出F_p。

事實上，使用這樣的配對如同提起一把雙面刃：一方面這代表著我們可以利用這種配對實現不同的協定，同時也代表了我們在選擇使用什麼橢圓曲線時要特別小心。

每個橢圓曲線都有一個叫embedding degree 的值──最小的整數k 使得p^k − 1 是n 的倍數（p 是體所用的質數，而n 則是曲線的階）。在上文提到的體當中k = 12 ，在傳統的橢圓曲線密碼學中（不在意配對的時候）使用的體的embedding degree 通常都會非常大，大到讓計算出配對這件事是計算上不可行的。不過，當我們不注意的時候很有可能會構建出k = 4 甚至k = 1 的體。

當k = 1 的時候，橢圓曲線上的「離散對數問題」（在只知道P = G * p 這個點的情況下，計算出p 的值；也就是你在「破解」橢圓曲線的私鑰時需要解的問題）可以退化成一個在F_p 上的相對簡單的問題（這方法叫做MOV attack）；使用一個embedding degree 大於等於12 的橢圓曲線會保證這種退化不可行，又或者是退化出來的問題複雜到至少跟用「正常」的方法從公鑰算出私鑰一樣困難。現在所有標準的曲線參數都經過仔細檢查，不會受這個問題影響。