椭圆曲线在三十余年来广泛使用于加密、数位签章等密码学应用。
撰文:Vitalik Buterin
发表时间:2017 年 1 月 14 日
密码学的众多基础建设,例如「确定性阈值签名」 (deterministic threshold signature,暂译)、zk-SNARKs 与其他形式较简单的零知识证明等等,背后关键的原始模型之一是椭圆曲线对。椭圆曲线在三十余年来广泛使用于加密、数位签章等密码学应用,「椭圆曲线对(EC pairings)」(或双线性映射)是最近基于其上的新玩意,它引进了加密乘法,让基于椭圆曲线的协定,所能做的事情大为增加。这篇文章会详细地介绍椭圆曲线对,以及简要解释它如何运作。
因为这概念真的不容易,不太预期你读第一遍甚至是第十遍时就真的完全理解,但希望这篇文章能至少告诉你一些箇中奥妙。
椭圆曲线本身就已经是一个不太容易理解的主题,但这篇文章大多时候会假设你对它的运作原理有些认识,如果你没有基本概念的话,我会推荐这篇文章作为入门。
总的来说,椭圆曲线处理的是一些称为「点(points)」的数学物件,直白说是二维平面上的点(x, y),以及一些加减运算的特别公式(例如计算R = P + Q),你还可以让点去乘以一个整数(例如P * n = P + P + … + P,虽然说在n 很大的时候有个快得多的算法)。
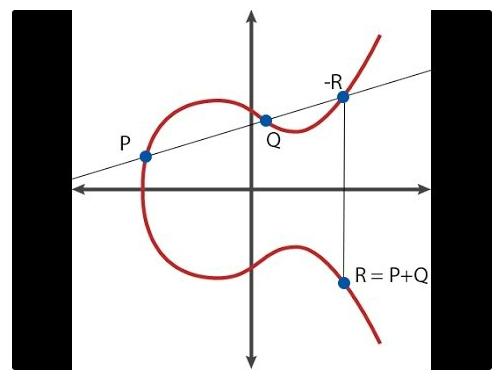
这是点的加法在图上看起来的样子
除此之外有个特别的点叫做「无穷远点」(O),在点的运算规则中作为零元素,也就是对于所有点都有P + O = P。一条曲线还拥有一个称为「阶(order)」的特质,也就是存在一个正整数n,对于所有P 都使得P * n = O(当然P * (n + 1) = P,P * ((7*n) + 5) = P * 5,以此类推)。还有某个事先协议好的「生成点(generator point) G」,也就是挑选来作为加法单位元素、代表数字1 那个角色的点。理论上任何曲线上的点都可以当生成元,重要的是那个G 是统一选定的。
配对就是进一步允许你验证某类更复杂的等式:例如,如果P = G * p、Q = G * q、R = G * r,当你要检查p * q = r 是否成立,你只要有P, Q, R 三个点的座标做为输入就行了。这也许看起来像是椭圆曲线最基本的安全保证被打破了,因为乍看之下,要是知道P 点的座标就泄漏了p 的值。但事实上这样泄漏的风险非常局限──准确来说,判定性的 Diffie-Hellman 问题很容易,但是计算性的版本仍然是「计算上不可行(computationally infeasible)」的。至少难度就跟不知道这个值差不多。
第三种理解「配对」的方式,也许是在我们讨论的大部分使用情境里最有启发性的方式是,如果你把椭圆曲线上的点看成一个单向加密函数(也就是说encrypt(p) = p * G = P),那么对比传统椭圆曲线的数学原理让你检验变数间的线性约束(例如P = G * p、Q = G * q、R = G * r,检验5 * P + 7 * Q = 11 * R 其实是在检验5 * p + 7 * q = 11 * r),椭圆曲线对就是让你检验变数间的二次约束(检验e(P, Q) * e(G, G * 5) = 1 其实是在检验p * q + 5 = 0)。能够做到二次以后,就足够让我们做些像是确定性阈值签名、QAP (quadratic arithmetic programs,一种零知识证明) 等等有趣的应用。
现在的问题是我们上面引进的e(P, Q) 这个运算子到底是什么?这就是一组「配对」。数学家们有时候也把它叫做「双线性映射」,「双线性」在这里基本上表示它满足以下条件:
e(P, Q + R) = e(P, Q) * e(P, R)
e(P + S, Q) = e(P, Q) * e(S, Q)
注意到这里的+ 和* 可以是任意的运算子;当你新建立一类数学物件的时候,抽象代数上不在意+ 和* 是如何被「定义」的,只要和我们习以为常的运算一致就可以了,像是a + b = b + a、(a * b) * c = a * (b * c)、(a * c) + (b * c) = (a + b) * c。
假如现在P, Q, R, S 仅仅是数字,那配对函数十分容易构造:我们可以定义e(x, y) = 2^(xy)。那么我们就会看到:
e(3, 4 + 5) = 2^(3 * 9) = 2²⁷
e(3, 4) * e(3, 5) = 2^(3 * 4) * 2^(3 * 5) = 2¹² * 2¹⁵ = 2²⁷
它确实是双线性的!
然而像这样简单的配对不适合用在密码学上,因为要分析单纯运作在整数上的数学物件简直轻而易举;整数的性质使得除法、对数等等许多操作变得容易。整数也没有「公钥」或是「单向函数」的概念。进一步说,上面描述的那种配对是可逆的:知道x、知道e(x, y),做个除法和对数就可以算出y。我们想要的数学结构是尽可能接近「黑盒子」:你可以做些加减乘除,但也就只能这样了。这个时候椭圆曲线和椭圆曲线对就派上用场了。
人们发现,确实能在椭圆曲线的点上设计双线性映射──也就是当输入是椭圆曲线上的两个点P 和Q,构造一个函数e(P, Q) 映射到一个F_p¹² 的元素(至少在这个特定情形下够用了,而这规范根据曲线的细节会有所不同,后面会再提到),但做到这件事情底下的数学实在是十分复杂。
第一,我们来介绍质数体(prime fields) 和扩体(extension fields)。上图画的曲线虽然漂亮,但那是在你假设曲线的等式定义在平常所用的实数上才会长成那样。如果我们真的在密码学里使用实数,那你就可以用对数「倒回去」,那一切就没用了,更何况储存实数所需的空间可能会无尽地长。因此,我们改用实数体上的数字。
一个质数体由数字0, 1, 2, …, (p−1) 所成集合构成,其中p 是一个质数,而其运算由下定义:
a + b: (a + b) % p
a * b: (a * b) % p
a - b: (a - b) % p
a / b: (a * b^(p-2)) % p
基本上,所有运算都在模(modulo) p 下进行(这里有模运算的简介)。除法是个特例。一般来说,3/2 不是整数,但我们想要只处理整数,所以我们改成去找整数x 使得x * 2 = 3,而这里的* 当然是指上面定义的模数乘法。幸亏有费马小定理,除法的那个指数定义能满足需要,但还有个更快的做法,那就是用扩展欧几里得演算法。假设p = 7,下面有几个例子:
2 + 3 = 5 % 7 = 5
4 + 6 = 10 % 7 = 3
2 - 5 = -3 % 7 = 4
6 * 3 = 18 % 7 = 4
3 / 2 = (3 * 2^5) % 7 = 5
5 * 2 = 10 % 7 = 3
如果你试着操作这样的运算,你会发现它是前后一致的,而且满足所有寻常的规则。最后的两个例子说明(a / b) * b = a,你还可以发现(a + b) + c = a + (b + c)、(a + b) * c = a * c + b * c,还有其他你高中所知道和喜爱的代数等式都还会继续运作。现实上使用的椭圆曲线,点和等式通常都是在质数体上运算的。
现在我们来谈谈扩体。你先前可能已经看过扩体了,数学课本上最常遇到的例子是复数体──以实数体为基础加入 sqrt(-1) = i 这个新的元素后扩张而成的。简单来说,扩体就是在一个现成的体上,「发明」一个新的元素,并且定义好这个新元素跟现有的元素的关系(在刚刚的例子里的话是i^2 + 1 = 0) ;这个关系式不能被现有的数字满足,那把这个新元素加进「旧有的元素的所有线性组合( linear combination )」组成的集合便是构造出来的集合。
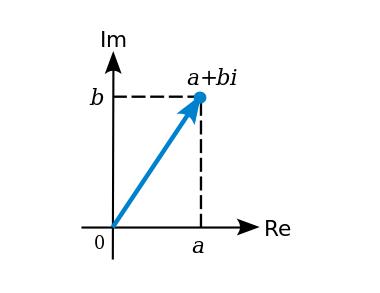
我们也可以对质数体进行扩张;举个例子,在模7 的质数体里加入我们刚刚所说的i,那么我们有
(2 + 3i) + (4 + 2i) = 6 + 5i
(5 + 2i) + 3 = 1 + 2i
(6 + 2i) * 2 = 5 + 4i
4i * (2 + i) = 3 + i
最后的等式可能比较难以理解;其实那条等式的第一步是先把左边的乘法做分配变成4i * 2 + 4i * i,得到8i - 4。因为我们是在模7 的环境下做运算,这个数字就变成了i + 3。至于除法的部份则是:
a / b : (a * b^(p^2-2)) % p
这边费马小定理的指数从p 变成了p² ,当然也可以使用扩展欧几里得演算法来更有效率地运算。因为对于在体中的任一个元素x 都会有x ^ (p² − 1) = 1 ,所以我们称(p² − 1) 为「体中乘法群的阶」。
对于实数体,代数基本定理保证了它的二次扩体(quadratic extension) :复数体,是完备的(译者注:应为代数封闭,实数体亦具有完备性但可以扩张)──这个体不能再被扩张,因为所有可能的新元素j 与现有的复数之间应该要满足的数学关系(严格来讲是以多项式来定义的数学关系),都有一个在体内的元素早已满足。但在质数体中,就没有这个问题,我们可以对其进行三次扩张(cubic extension)(新元素w 与现有元素的关系式是一条三次多项式,因此1, w , w² 是线性独立(linear independent) 的),高次扩张,甚至扩张再扩张等等。椭圆曲线就是建立在这些模运算的复数上的。
对这些数学如何实作成程式码有兴趣的话,这边有一些实作质数体以及扩体的例子。
回头来看椭圆曲线对。椭圆曲线对(我们这边讨论的配对只是其中一种,但配对的逻辑是相近的)是一个G2 × G1 → Gt 的映射,其中:
- G1是一条椭圆曲线,线上的点满足形如y² = x³ + b 的式子,而且点的x, y 座标都是F_p 的元素(也就是说他们只是普通的数字,但算术运算会在模某个质数下进行)。
- G2也是一条椭圆曲线,同样满足G1 的曲线,但G2 中的元素的x, y座标是F_p¹² 的元素(这是我们刚才讲到的那些复数;我们定义一个神奇数字w,它满足一个12 次多项式w¹² − 18 w⁶ + 82 = 0)
- Gt是椭圆曲线的运算结果形成的集合。在我们讨论的曲线中,Gt 是F_p¹²(跟G2 用一样的那些复数)
它主要必须满足的性质是双线性,在这个脉络下这样代表:
e(P, Q + R) = e(P, Q) * e(P, R)
e(P + Q, R) = e(P, R) * e(Q, R)
(译者注:这边的双线性准确来说是「整数上的双线性(bilinearity over ℤ)」,只是因为这里所讨论的椭圆曲线上的点都是整数点,而且乘法和加法的定义是整数运算完再取模,自然已经满足一些线性性质)
选择配对函数还有两个重要的准则:
- 运算要足够有效率(例如我们可以直接对所有点取离散对数然后全部乘起来,作为一种简单的配对方法,但这所需要的运算成本和破解椭圆曲线密码学一样困难,所以这不算)
- 非退化(你当然可以单纯地定义e(P, Q) = 1,但它并不是一个特别有用的配对)
所以我们该怎么做到这件事?
让配对函数得以运作背后的数学十分困难,而且需要一些进阶的代数,超过我们目前为止所见,但我会大致说明。首先我们需要定义「因子(divisor)」的概念,基本上是另一种方式来表示作用在椭圆曲线上的点的函数们。一个函数的因子基本上计算了一个函数有多少个零点和取值无限大的点。为了理解清楚一些,我们来看看几个例子。让我们选定一个点P = (P_x, P_y),然后考虑以下函数:
f(x, y) = x − P_x
它的因子是[P] + [−P] − 2 * [O] (这里的方括号用来表示某个点出现在函数的零点和取值无限大的点所成集合,而不是那个点本身;[P] + [Q] 和[P + Q]并不相同)。原因如下:
- 这个函数在P 点的值等于零,因为x 取值P_x,所以x − P_x = 0
- 这个函数在−P 点的值等于零,因为−P 和P 的x 座标相同
- 这个函数在x 趋向无限大的时候也趋向无限大,所以我们说这个函数在O 点取值无限大。计算这个无穷远点要算两次,所以O 要乘以乘数-2(负号是因为它是无穷远点而有别于零点,2 是因为它要被算两次)。
计算上的理由大约是:因为这个曲线的方程式是x³ = y² + b,当x 增加,为了让y² 达到相当的规模,y 增长的速度大约需要是x 的1.5 倍。因此如果一个线性函数只包含x,那它无限大那一项的乘数是2,但如果它包含y,那乘数就要是3。
现在考虑一条线的函数:
ax + by + c = 0
其中a, b, c 被选定来让这条线通过点P 和点Q。根据椭圆曲线加法的运作方式,它也一定会通过−P−Q 这个点。因为它跑向无限大时会同时取决于x 和y,所以因子是[P]+ [Q] + [−P−Q] − 3 * [O]。
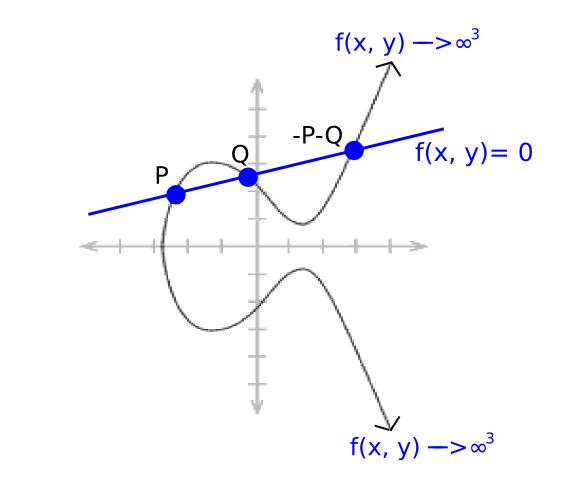
我们知道所有「有理函数」(也就是点座标经过有限次加减乘除运算定义出来的函数)唯一地对应到某个因子,顶多就是多乘一个常数(也就是如果两个函数F 和G 有相同的因子,那么必存在常数k 使得F = G * k)。
对于任意两个函数F 和G,(F * G) 的因子等于F 和G 的因子之和(数学课本上你会看到(F * G) = (F) + (G)),所以比如f(x, y) = P_x − x,那么(f³) = 3 * [P] + 3 * [−P] − 6 * [O];P 和−P 算三次是因为在特定的数学意义下f³ 会「三倍快地」靠近0。
留意有个定理说如果你把某个因子的「方括号」拿掉,那些点运算后的结果必定是O([P] + [Q] + [−P−Q] − 3 * [O] 照着操作会得到P + Q − P − Q − 3 * O = O),而且任何有这个性质的因子就会是那个函数的因子。
现在我们可以开始看Tate pairing 了。考虑以下用因子定义的函数:
- (F_P) = n * [P] − n * [O],其中n 是G1 的阶数,也就是对于所有P,n * P = O
- (F_Q) = n * [Q] − n * [O]
- (g) = [P + Q] − [P] − [Q] + [O]
现在,让我们看看这个乘积F_P * F_Q * g^n。它的因子是:
n * [P] − n * [O] + n * [Q] − n * [O] + n * [P + Q] − n * [P] − n * [Q] + n * [O]
化简会得到干净的:
n * [P + Q] − n * [O]
注意到这个因子的格式跟F_P 和F_Q 的因子相符。因此有F_P * F_Q * g^n = F_(P + Q)。
现在再多做一个称为「最终指数(final exponentiation)」的操作,把前述运算的结果(F_P, F_Q 等等)自乘到z = (p¹² − 1) / n 的幂次,其中p¹² − 1 是F_p¹² 中乘法群的阶(换句话说就是对于所有x ϵ F_p¹², x^(p¹² − 1) = 1)。注意到如果你把这个指数套用在任何已经是n 次幂的结果上,你就会得到某个元素的(p¹² − 1) 次方,结果就会变成1。因此,在最后的指数步骤后,g^n 会消掉,然后我们就会得到F_P^z * F_Q^z = F_(P + Q)^z。于是就有了双线性的性质的一部分。
现在如果你想构造一个函数,它在两个参数上都会是双线性的,你需要更吓人的数学,那么要做的不只是算F_P,还要计算F_P 的因子,再做下去就会得到完整的Tate pairing。为了证明更多结论你需要理解一些概念像是「线性等价(linear equivalence) 」以及Weil reciprocity 之类。这些概念详细的内容可以在这里以及这里看到。
而这边实作了一个Tate pairing 的修改版── Optimal Ate Pairing。该代码里还实现了用米勒算法来计算出F_p。
事实上,使用这样的配对如同提起一把双面刃:一方面这代表着我们可以利用这种配对实现不同的协定,同时也代表了我们在选择使用什么椭圆曲线时要特别小心。
每个椭圆曲线都有一个叫embedding degree 的值──最小的整数k 使得p^k − 1 是n 的倍数(p 是体所用的质数,而n 则是曲线的阶)。在上文提到的体当中k = 12 ,在传统的椭圆曲线密码学中(不在意配对的时候)使用的体的embedding degree 通常都会非常大,大到让计算出配对这件事是计算上不可行的。不过,当我们不注意的时候很有可能会构建出k = 4 甚至k = 1 的体。
当k = 1 的时候,椭圆曲线上的「离散对数问题」(在只知道P = G * p 这个点的情况下,计算出p 的值;也就是你在「破解」椭圆曲线的私钥时需要解的问题)可以退化成一个在F_p 上的相对简单的问题(这方法叫做MOV attack);使用一个embedding degree 大于等于12 的椭圆曲线会保证这种退化不可行,又或者是退化出来的问题复杂到至少跟用「正常」的方法从公钥算出私钥一样困难。现在所有标准的曲线参数都经过仔细检查,不会受这个问题影响。
 ONDO0.39 -3.11%
ONDO0.39 -3.11%
 TRUMP5.10 -1.04%
TRUMP5.10 -1.04%
 SUI1.44 -1.16%
SUI1.44 -1.16%
 TON1.46 -3.57%
TON1.46 -3.57%
 TRX0.28 -0.87%
TRX0.28 -0.87%
 DOGE0.13 -0.83%
DOGE0.13 -0.83%
 XRP1.87 -1.93%
XRP1.87 -1.93%
 SOL125.56 -0.61%
SOL125.56 -0.61%
 BNB845.93 0.03%
BNB845.93 0.03%
 ETH2959.78 0.29%
ETH2959.78 0.29%
 BTC87802.50 -0.68%
BTC87802.50 -0.68%







 个人中心
个人中心 退出登录
退出登录




 首页
首页 深潮精选
深潮精选 Research
Research 项目发现
项目发现 7x24h︎快讯
7x24h︎快讯 最新活动
最新活动
 分享至微信
分享至微信



 原文链接
原文链接 添加收藏
添加收藏 分享社交媒体
分享社交媒体
 @VitalikButerin
@VitalikButerin 精选解读
精选解读

 波兰众议院再次通过《加密资产市场法案》,将被否决议案重新送交参议院
波兰众议院再次通过《加密资产市场法案》,将被否决议案重新送交参议院







 扫码关注公众号
扫码关注公众号





