随着市场在熊市中的沉寂，投资者和项目方总会开始寻找新的成长点。

在缺乏持续性热点的空窗期，正是探索和深入了解新技术的绝佳机会，因为新技术可能会成为下一个市场叙事的核心。

上个月，知名的加密风投公司 Portal Ventures 在其官方博客上发布了一篇详细探讨全同态加密（FHE）技术的文章。然而，这篇深入的技术文章似乎并没有引起大众的广泛关注。

Portal Ventures的作者这样说到："全同态加密是加密方案的圣杯"。

理解 VC 关注的技术对于投资者来说至关重要，因为它可以帮助我们预测和理解下一个市场周期的潜在趋势。事实上，同态加密、零知识证明和多方安全计算等技术在密码学领域都有深远的影响，尤其是全同态加密，它在加密货币和web3领域可能都有巨大的应用潜力。

但问题是，大多数人对于全同态加密的真正意义、如何工作以及与其他技术的区别都知之甚少。在市场不景气，投资情绪低迷的时候，跳出炒作的喧嚣，深入研究和了解这些前沿技术，无疑是一个明智的选择。

有些巧合的是，笔者在数年前有幸在工作中接触过与FHE相关的技术解决方案。因此决定对 Portal Ventures 的这篇文章进行深入的解读，希望为大家提供一些新的视角和思考。

同态与全同态加密，到底是个啥？

如果直接看 Portal Ventures 的原文，您可能会对全同态加密（FHE）的复杂数学描述感到困惑。

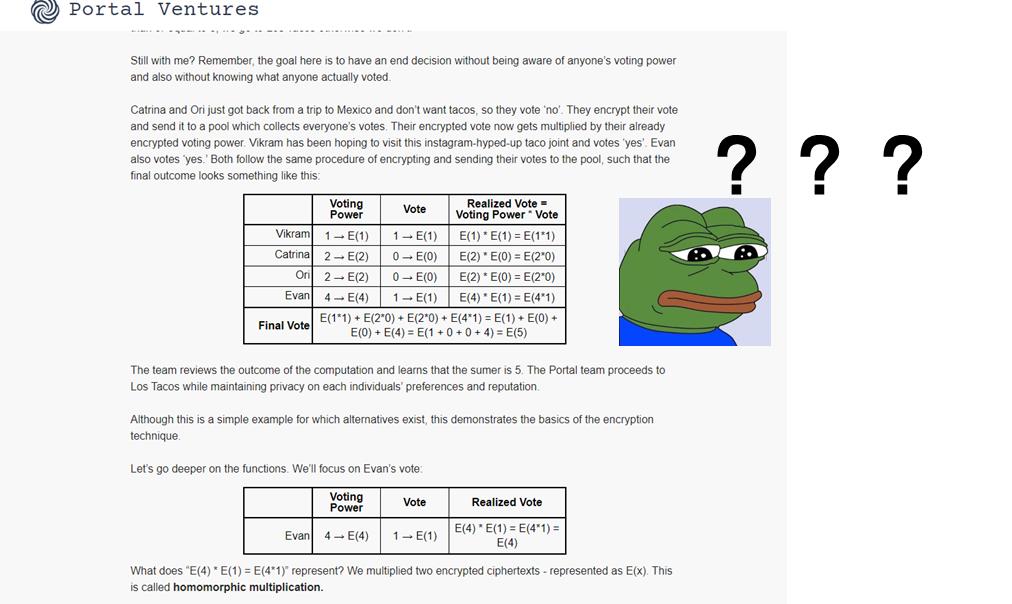
事实上，密码学的世界充满了深奥和技术性，但我们完全可以用简单和通俗的方式来解释这些概念。在这一节中，笔者试图为您提供一些更直观、更易于理解的例子，帮助您深入了解全同态加密。

首先，想象一个“秘密魔盒”。您可以将任何物品放入这个盒子，并锁定它。一旦锁定，您就不能看到或触摸盒子里的内容。但是，令人惊奇的是，这个魔盒允许您在不打开它的情况下，改变里面物品的颜色或形状。

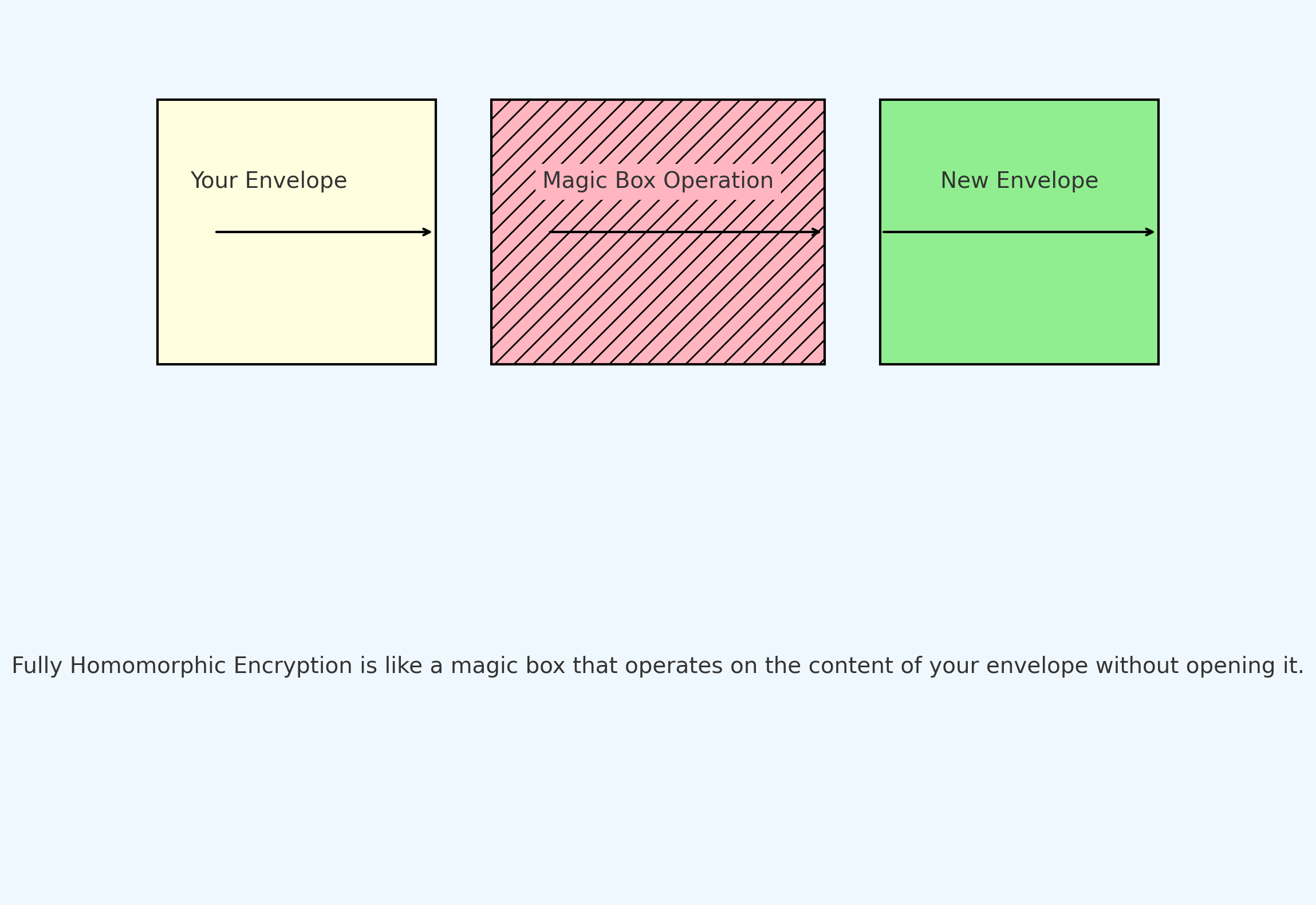
如上图所示，全同态加密（Fully Homomorphic Encryption）可以被视为一个魔法盒子：

1. 你的信封 (Your Envelope): 这代表你想加密的原始数据。

2. 魔法盒子操作 (Magic Box Operation): 即使不解密或打开信封，你也可以在信封里的数据上进行操作（如加、减等计算）。

3. 新的信封 (New Envelope): 经过魔法盒子操作后，你会得到一个新的加密结果。

这就是同态加密的基本思想：在不了解数据本身的情况下，也能对加密的数据进行操作。

这个通俗的例子有助于搞清楚"全同态加密"在干什么。但实际上，这个概念本身还是有点听君一席话如听一席话。那么，什么又叫做“全”和“同态”？

1. 什么叫做“全”（Fully）?

• 在密码学中，加密方案可以支持多种操作，比如加法、乘法等。当我们说一个加密方案是“全同态”的，我们意味着这个加密方案支持在加密数据上进行任意数目的基本运算（例如加法和乘法）而不需要解密。这与部分同态加密（如只支持加法或只支持乘法的方案）形成对比。

2. 什么叫做“同态”（Homomorphic）?

• "同态"来自于希腊文，意思是“相同的形状或结构”。在密码学中，当我们说加密方案是同态的，意味着有些运算在明文上的效果与在密文上的效果是一样的。换句话说，如果你在加密的数据上进行某种运算，然后解密结果，这和你先解密数据然后在解密后的数据上进行相同的运算是等价的。

3. 例如，考虑一个支持同态加法的加密方案。假设你有两个数字：3 和 4。你可以先加密这两个数字，然后使用这个同态加密方案将两个加密的数字相加。最后，你解密相加后的结果。得到的解密结果将是7，这与你直接在明文3和4上相加得到的结果是一样的。

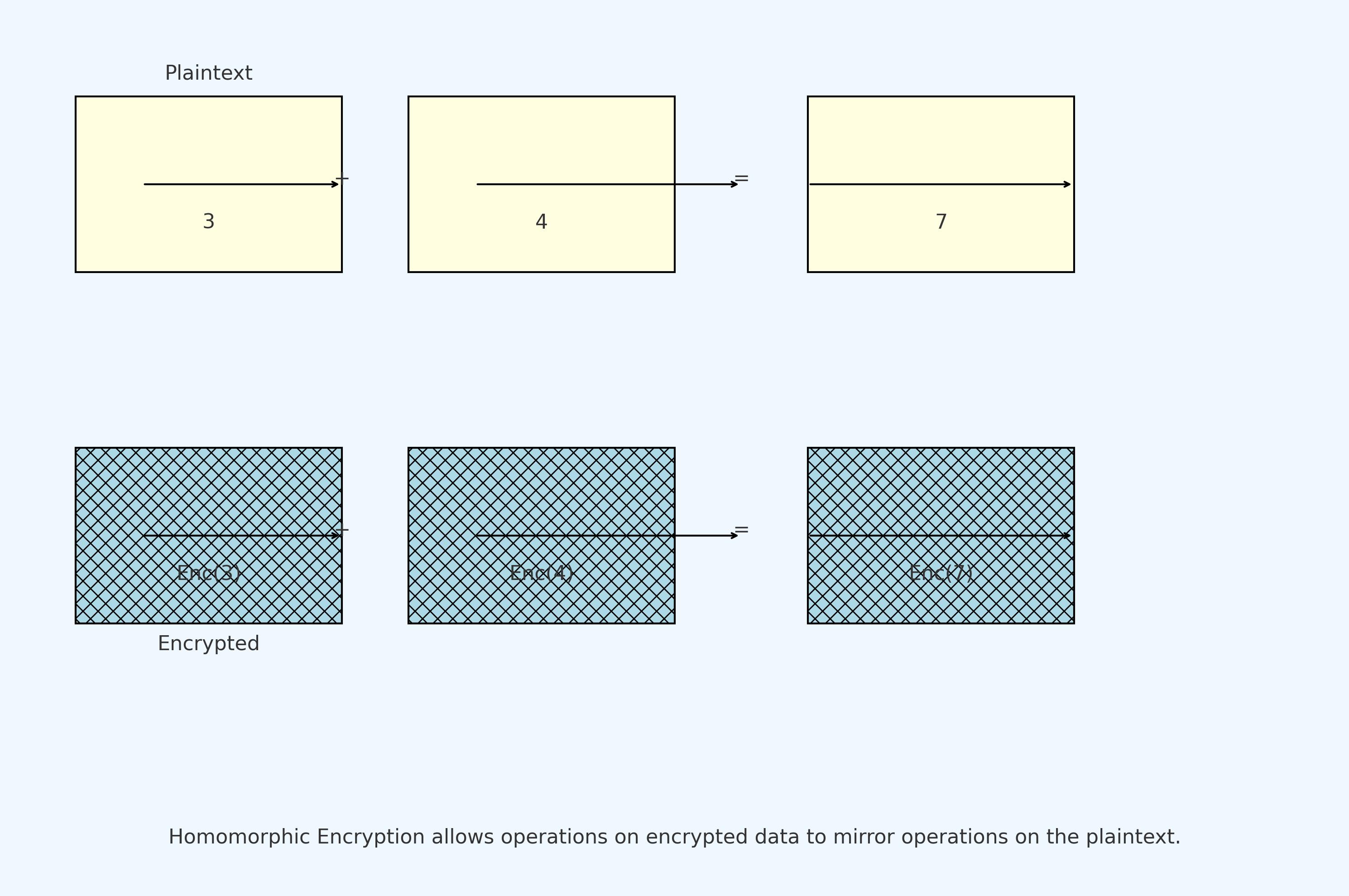
但是，您可能会问，我们如何在非数字上进行这些加减乘除操作呢？实际上，我们可以使用特定的编码方法将非数字数据转化为数字形式，从而在它们上进行加法和乘法等运算。这意味着全同态加密的应用不仅仅限于数学计算，它还可以被广泛应用于其他领域。

为了更直观地解释这个概念，让我们考虑医疗数据的例子。

1. 假设医院有一些患者数据，比如年龄和血糖值，但出于隐私考虑不希望直接发送给云服务提供商进行分析。

2. 通过使用全同态加密，医院可以先将这些数据加密。

3. 想象一下，云服务提供商需要计算所有患者的平均年龄（这需要加法和除法）和血糖值的总和与患者数量的乘积（这涉及加法和乘法）。

4. 所有这些计算都可以在加密的数据上完成，而无需解密。云服务提供商在不解密数据的情况下完成计算，然后将加密的结果返回给医院。这确保了数据的隐私，同时也满足了数据处理的需求。

这就是全同态加密的魅力所在，它为我们提供了一个既安全又灵活的数据处理方法。

为何FHE很重要？

当前，对加密数据进行计算的现有方法并不理想。它们在资源使用和时间消耗上都相对昂贵。

因此，行业标准流程是，在进行计算之前，由第三方（即公司）对数据进行解密。

以一个具体的例子来说，想象一下您有一个数据文件，其中包含一些高调个体的财务信息。

• 我们称这个文件为“M”。我们需要某个公司对这些数据进行分析。

• 目前的流程是怎样的呢？首先，我使用如RSA或AES这样的加密函数对M进行加密。此时，M变成了E(M)，其中E是加密函数。

• 接下来，我将E(M)发送给公司服务器。公司现在通过相关的解密函数D来解密E(M)为明文，即D(M)。

• 公司直接对文件M进行明文进行分析操作。

• 操作完后，再把M加密一次，生成一个E(M')。

• 公司再把加密的M'并将其发送回给我，然后我再次解密它。

发现了吗，这里的关键问题在于，当公司解密M并将其存储在其服务器上进行计算时，第三方可以访问原本应受保护的敏感数据。如果该人员遭到黑客攻击或有恶意意图，这就会引发问题。

全同态加密（FHE）通过允许对加密数据进行计算来解决此问题。公司不再需要解密E(M)。它直接在加密数据上进行分析。没有解密的需要，也不需要信任假设。

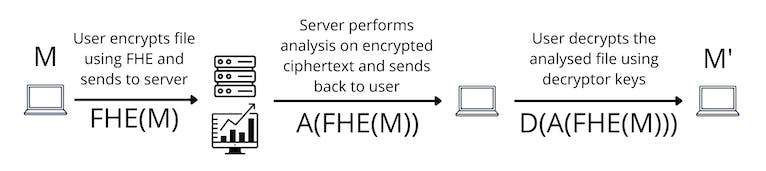
综上所述，全同态加密的引入解决了当前数据处理流程中的一个关键问题，即在第三方处理数据时可能暴露的隐私风险。FHE为我们提供了一个在保证数据隐私的同时，有效地处理加密数据的方法。

FHE在Crypto中如何应用？

全同态加密（FHE）为加密世界开启了一扇新的大门，为我们带来了许多之前无法想象的应用场景。Poly Venture的原文对场景的描述比较简单，我们试着用一张表更有条理的做出了一个解读。

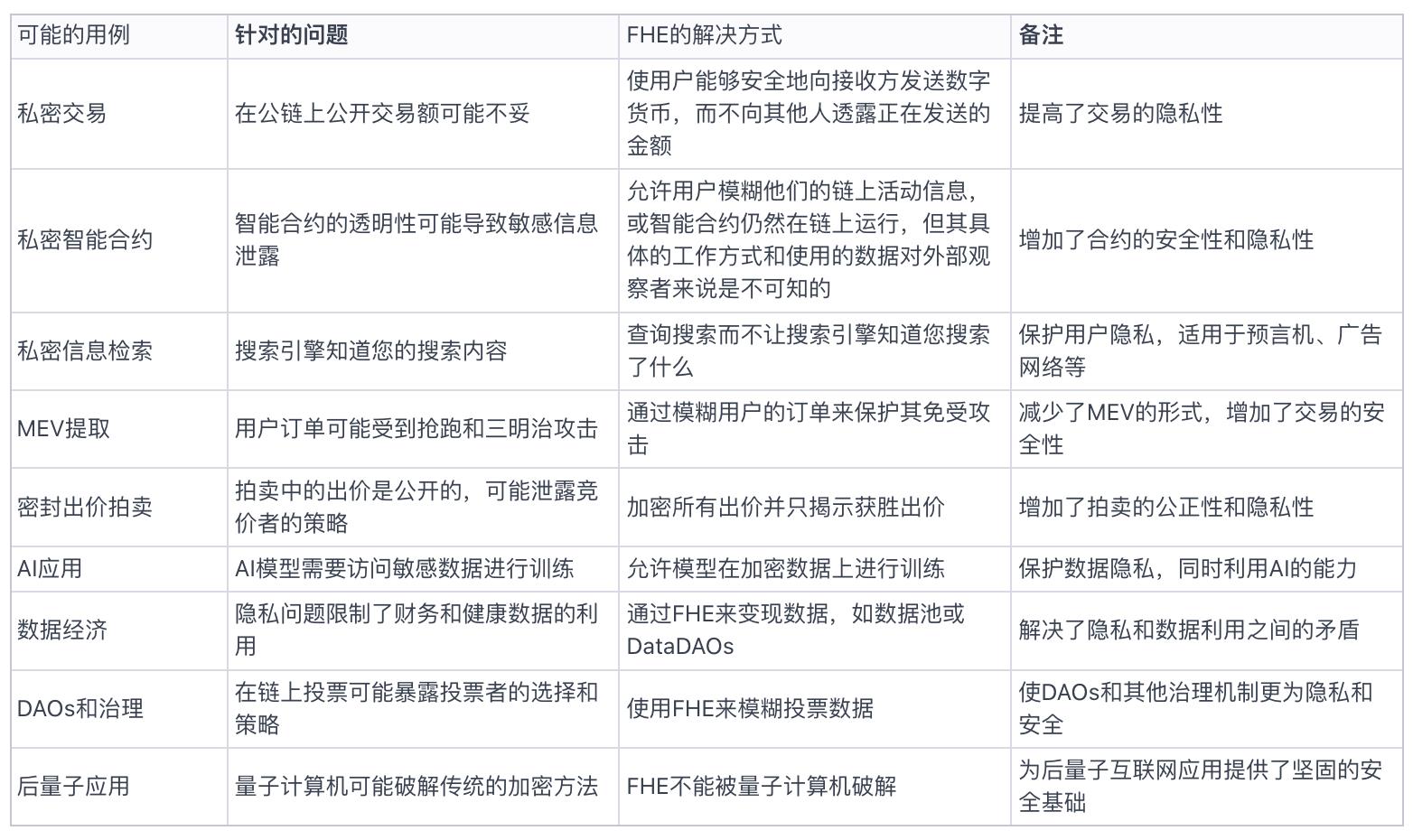
FHE vs ZK vs MPC，傻傻分不清？

在了解了全同态加密（FHE）后，很容易将其与其他熟悉的技术，如零知识证明（ZK）和多方计算（MPC）相提并论。乍一看，它们似乎都致力于解决相似的隐私和计算问题。但这三者之间实际上有哪些联系和区别呢？

首先，我们先了解一下这三种技术的基本定义：

• FHE：允许在加密数据上执行计算，而无需解密。

• ZK：允许一方向另一方证明某个陈述是真实的，而无需揭示任何关于该陈述的具体信息。

• MPC：使多方能够共同在他们的私有数据上执行计算，而不向其他参与者泄露输入数据。

然后，让我们从多个维度来看看他们的异同和交集：

1. 目的：

• FHE的主要目的是在不解密的情况下进行计算。

• ZK的目标是证明一个事实的正确性而不泄露有关该事实的任何信息。

• MPC的目标是允许多方安全地共同计算，而不泄露各自的输入。

2. 隐私与计算：

• 在ZK中，计算不一定是私有的。例如，尽管你可以使用ZK来验证银行账户余额是否超过100,000美元，但进行这样的验证的计算不一定是私有的。

• 与此相反，FHE确保了计算的隐私性，因为所有的计算都在加密数据上进行。

3. 限制与挑战：

• MPC需要至少一个诚实的服务器，并且可能受到DDoS攻击、沉默合谋攻击和通信开销的影响。

• ZK主要用于证明正确性，而不是隐私技术。

• FHE尽管提供了强大的隐私，但计算效率较低，对资源的需求较大。

4. 在加密领域的应用：

• FHE可以用于构建更加隐私的智能合约和其他区块链应用。

• ZK被用于创建可扩展的区块链解决方案，如zk-rollups。

• MPC主要用于私钥管理和托管。

5. 交叉使用：

• MPC可以与FHE结合，形成阈值FHE，通过将一个FHE加密密钥分割成多个，并给每个参与者一个来增强安全性。

• zkFHE是零知识证明和全同态加密的结合，正在被研究，以实现在FHE智能合约上的zk-rollups。

总体来说，尽管FHE、ZK和MPC在某些方面有所重叠，但它们都有各自独特的优势和应用场景。在加密世界中，这三种技术都为增强隐私和安全性提供了巨大的潜力，但它们的结合和进一步的研究仍然是加密社区的一个活跃领域。

最后，我们也可以给出一张省流版的表格，将上述技术放在一起进行比较，帮助大家更加直观的进行理解。

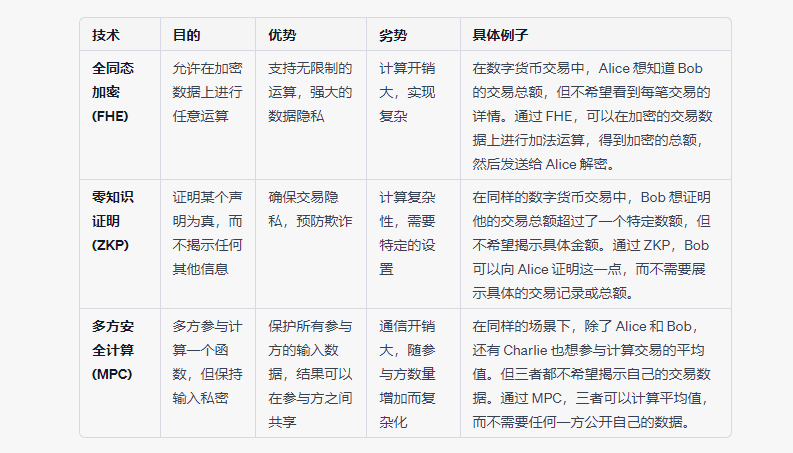
FHE的未来展望

通过上文可以感觉到，全同态加密（FHE）显然是一种强大的技术。

但为什么它还没有被广泛采用，甚至在加密CT中很少提及？一方面由于理解技术本身有一定门槛，另一方面则在于FHE技术目前还面临一些挑战，难以轻松以商业化形态走进大众视野。

面临的挑战可能有：

1. 计算密集：当我们的密文互相作用时，为了维持安全性，会添加更多的噪声。FHE方案使用“自举”技术来减少噪声，但这非常计算密集，资源消耗很大。

2. 功能有限：FHE的计算仅限于加法、乘法及其变种/组合。例如，不能在FHE中使用if语句，因为内容是加密的。此外，构建相对复杂的操作，如比较和除法，需要仔细规划基本逻辑，这导致了更复杂的编程技巧和计算效率较低。

3. 兼容性/组合性问题：现有的应用程序和服务提供商并不是为了在加密数据上进行计算而构建的。这限制了FHE与现有技术的整合，并增加了开发FHE兼容应用所需的惯性。

可能的解决方案：

1. 硬件加速器：某些FHE方案，如nuFHE和cuFHE，可以使用GPU加速，但主要的突破将来自更快的FPGA和ASIC。其他技术，如光子技术，也正在被研究，以加速FHE的硬件用例。

2. 新的编程范式：就像在Python上用于复杂数学的包如pandas和numpy，FHE库也将被构建。目前，Zama和Sunscreen是两个为FHE构建此类库和SDK的项目。此外，还需要构建专门的编译器，以使开发人员能够统一FHE、ZKP和MPC。

3. FHE与现有解决方案之间的整合：将构建解决方案，使现有工具与FHE兼容，作为工具和FHE加密数据之间的中间层。

最后，Portal Ventures在原文的结论部分再次强调：

“FHE是计算的圣杯，我们正在接近它的商业化。价值和计算正在向开放、无需许可的网络过渡，我们相信FHE将支撑大部分所需的基础设施和应用程序”。

此外，它们也表达了对于目前正在研究FHE的项目的兴趣。因此，我们可以看到的是，VC对FHE有兴趣，或者说VC会率先对尚未走进大众视野的硬核技术感兴趣。

历史表明，基于新技术的加密项目，往往都带有闪亮的光环和较高的估值，并且受到各路资本的追捧。

在下一场盛宴开始前，我们的确应该多花时间，提前研究入场嘉宾的身份，才能在宴会开始时应对自如。